最新陕西中考数学真题含答案Word文档下载推荐.docx
《最新陕西中考数学真题含答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《最新陕西中考数学真题含答案Word文档下载推荐.docx(26页珍藏版)》请在冰豆网上搜索。
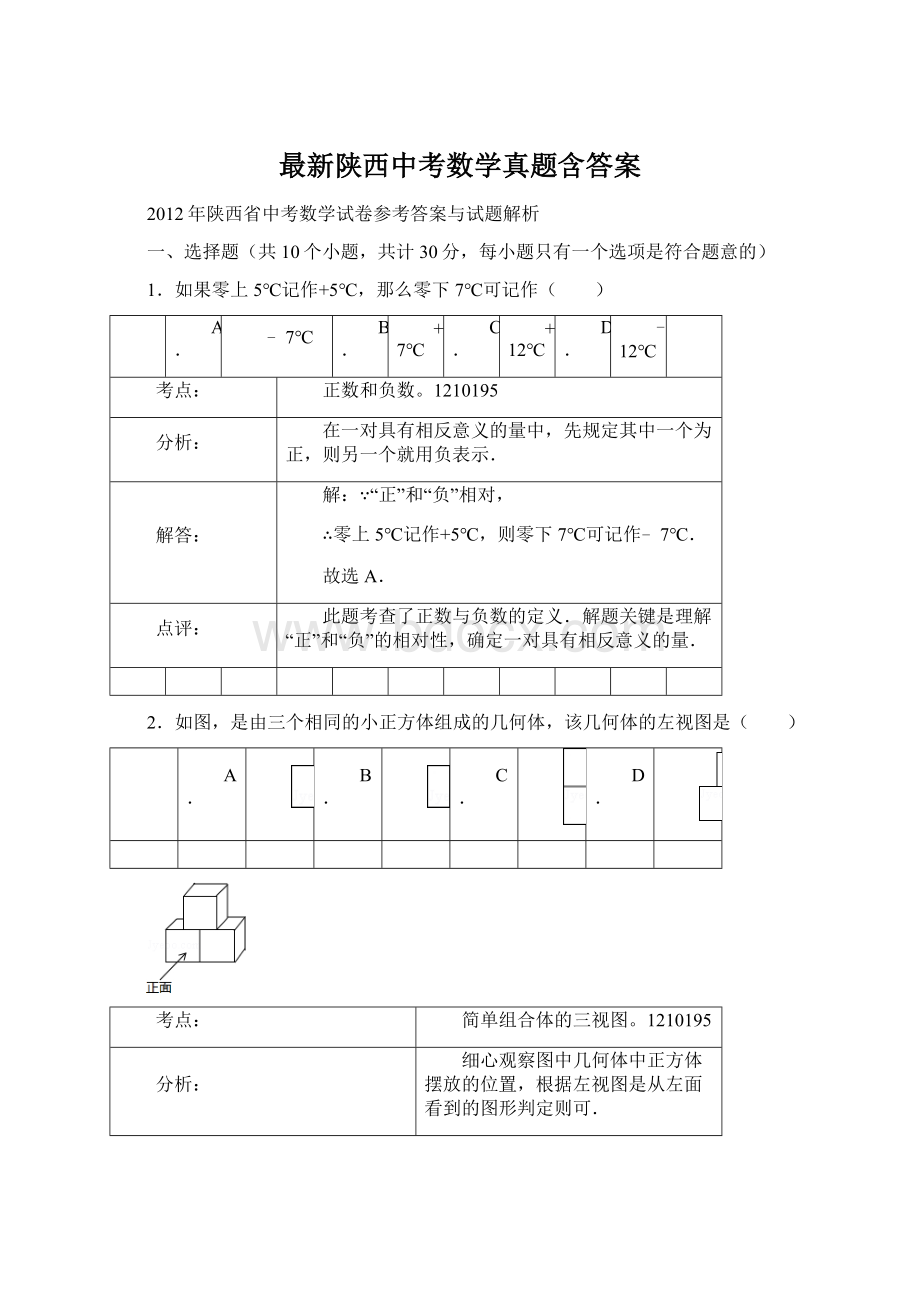
∴零上5℃记作+5℃,则零下7℃可记作﹣7℃.
故选A.
点评:
此题考查了正数与负数的定义.解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
2.如图,是由三个相同的小正方体组成的几何体,该几何体的左视图是( )
简单组合体的三视图。
细心观察图中几何体中正方体摆放的位置,根据左视图是从左面看到的图形判定则可.
从左边看竖直叠放2个正方形.
故选C.
考查了几何体的三种视图和学生的空间想象能力,左视图是从物体左面看所得到的图形,解答时学生易将三种视图混淆而错误的选其它选项.
3.计算(﹣5a3)2的结果是( )
﹣10a5
10a6
﹣25a5
25a6
幂的乘方与积的乘方。
利用积的乘方与幂的乘方的性质求解即可求得答案.
(﹣5a3)2=25a6.
故选D.
此题考查了积的乘方与幂的乘方的性质.注意幂的乘方法则:
底数不变,指数相乘;
积的乘方法则:
把每一个因式分别乘方,再把所得的幂相乘.
4.某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打分情况(满分100分)如表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( )
分数(分)
89
92
95
96
97
评委(位)
1
2
92分
93分
94分
95分
加权平均数。
先去掉一个最低分去掉一个最高分,再根据平均数等于所有数据的和除以数据的个数列出算式进行计算即可.
由题意知,最高分和最低分为97,89,
则余下的数的平均数=(92×
2+95×
2+96)÷
5=94.
本题考查了加权平均数,关键是根据平均数等于所有数据的和除以数据的个数列出算式.
5.如图,△ABC中,AD、BE是两条中线,则S△EDC:
S△ABC=( )
1:
2:
3
4
相似三角形的判定与性质;
三角形中位线定理。
在△ABC中,AD、BE是两条中线,可得DE是△ABC的中位线,即可证得△EDC∽△ABC,然后由相似三角形的面积比等于相似比的平方,即可求得答案.
∵△ABC中,AD、BE是两条中线,
∴DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴△EDC∽△ABC,
∴S△EDC:
S△ABC=()2=.
此题考查了相似三角形的判定与性质与三角形中位线的性质.此题比较简单,注意中位线的性质的应用,注意掌握相似三角形的面积的比等于相似比的平方定理的应用是解此题的关键.
6.在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
(2,﹣3),(﹣4,6)
(﹣2,3),(4,6)
(﹣2,﹣3),(4,﹣6)
(2,3),(﹣4,6)
一次函数图象上点的坐标特征。
专题:
探究型。
由于正比例函数图象上点的纵坐标和横坐标的比相同,找到比值相同的一组数即可.
A、∵=,∴两点在同一个正比例函数图象上;
B、∵≠,∴两点不在同一个正比例函数图象上;
C、∵≠,∴两点不在同一个正比例函数图象上;
D、∵≠,两点不在同一个正比例函数图象上;
本题考查了一次函数图象上点的坐标特征,知道正比例函数图象上点的纵坐标和横坐标的比相同是解题的关键.
7.如图,在菱形ABCD中,对角线AC与BD交于点O,OE⊥AB,垂足为E,若∠ADC=130°
,则∠AOE的大小为( )
75°
65°
55°
50°
菱形的性质。
先根据菱形的邻角互补求出∠BAD的度数,再根据菱形的对角线平分一组对角求出∠BAO的度数,然后根据直角三角形两锐角互余列式计算即可得解.
在菱形ABCD中,∠ADC=130°
,
∴∠BAD=180°
﹣130°
=50°
∴∠BAO=∠BAD=×
=25°
∵OE⊥AB,
∴∠AOE=90°
﹣∠BAO=90°
﹣25°
=65°
.
故选B.
本题主要考查了菱形的邻角互补,每一条对角线平分一组对角的性质,直角三角形两锐角互余的性质,熟练掌握性质是解题的关键.
8.在同一平面直角坐标系中,若一次函数y=﹣x+3与y=3x﹣5的图象交于点M,则点M的坐标为( )
(﹣1,4)
(﹣1,2)
(2,﹣1)
(2,1)
两条直线相交或平行问题。
计算题。
联立两直线解析式,解方程组即可.
联立,
解得,
所以,点M的坐标为(2,1).
本题考查了两条直线的交点问题,通常利用联立两直线解析式解方程组求交点坐标,需要熟练掌握.
9.如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
图1-4大学生购买手工艺制品目的C.
众上所述,我们认为:
我们的创意小屋计划或许虽然会有很多的挑战和困难,但我们会吸取和借鉴“漂亮女生”和“碧芝”的成功经验,在产品的质量和创意上多下工夫,使自己的产品能领导潮流,领导时尚。
在它们还没有打入学校这个市场时,我们要巩固我们的学生市场,制作一些吸引学生,又有使学生能接受的价格,勇敢的面对它们的挑战,使自己立于不败之地。
据统计,上海国民经济持续快速增长。
03全年就实现国内生产总值(GDP)6250.81亿元,按可比价格计算,比上年增长11.8%。
第三产业的增速受非典影响而有所减缓,全年实现增加值3027.11亿元,增长8%,增幅比上年下降2个百分点。
这里有营业员们向顾客们示范着制作各种风格炯异的饰品,许多顾客也是学得不亦乐乎。
据介绍,经常光顾“碧芝”的都是些希望得到世界上“独一无二”饰品的年轻人,他们在琳琅满目的货架上挑选,然后亲手串连,他们就是偏爱这种DIY的方式,完全自助在现场,有上班族在里面精挑细选成品,有细心的小女孩在仔细盘算着用料和价钱,准备自己制作的原料。
可以想见,用本来稀奇的原料,加上别具匠心的制作,每一款成品都必是独一无二的。
而这也许正是自己制造所能带来最大的快乐吧。
垂径定理;
勾股定理。
作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OM的长.
作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
PS:
消费者分析由垂径定理、勾股定理得:
OM==3,
在调查中我们注意到大多数同学都比较注重工艺品的价格,点面氛围及服务。
∵弦AB、CD互相垂直,
∴∠DPB=90°
虽然调查显示我们的创意计划有很大的发展空间,但是各种如“漂亮女生”和“碧芝”等连锁饰品店在不久的将来将对我们的创意小屋会产生很大的威胁。
∵OM⊥AB于M,ON⊥CD于N,
3、消费“多样化”∴∠OMP=∠ONP=90°
合计50100%∴四边形MONP是矩形,
∴OP=3
(二)对“碧芝”自制饰品店的分析本题考查了垂径定理及勾股定理的知识,解题的关键是正确地作出辅助线.
10.在平面直角坐标系中,将抛物线y=x2﹣x﹣6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值为( )
6
二次函数图象与几何变换。
计算出函数与x轴、y轴的交点,将图象适当运动,即可判断出抛物线移动的距离及方向.
当x=0时,y=﹣6,故函数与y轴交于C(0,﹣6),
当y=0时,x2﹣x﹣6=0,即(x+2)(x﹣3)=0,
解得x=﹣2或x=3,
即A(﹣2,0),B(3,0);
由图可知,函数图象至少向右平移2个单位恰好过原点,
故|m|的最小值为2.
本题考查了二次函数与几何变换,画出函数图象是解题的关键.
二、填空题(共6小题,每小题3分共18分)
11.计算2cos45°
﹣3+(1﹣)0= ﹣5+1 .
考点
实数的运算;
零指数幂;
特殊角的三角函数值。
先将二次根式化为最简,再计算零指数幂,然后代入cos45°
的值即可得出答案.
原式=2×
﹣3×
2+1=﹣5+1.
故答案为:
﹣5+1.
此题考查了实数的运算、零指数幂及特殊角的三角函数值,属于基础题,注意各部分的运算法则,另外要注意熟记一些特殊角的三角函数值.
12.分解因式:
x3y﹣2x2y2+xy3= xy(x﹣y)2 .
提公因式法与公式法的综合运用。
先提取公因式,再利用完全平方公式进行二次分解因式.
x3y﹣2x2y2+xy3,
=xy(x2﹣2xy+y2),
=xy(x﹣y)2.
本题主要考查提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
13.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A、在平面中,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°
,则线段AB扫过的面积为 π .
B、用科学记算器计算:
sin69°
≈ 2.47 (精确到0.01).
扇形面积的计算;
计算器—三角函数。
A、画出示意图,根据扇形的面积公式求解即可;
B、用计算器计算即可.
A、
由题意可得,AM=MB=AB=2,
线段AB扫过的面积为扇形MCB和扇形MAB的面积和,
故线段AB扫过的面积=+=.
B、sin69°
≈2.47.
、2.47.
此题考查了扇形的面积计算及计算器的运用,解答A需要我们明确线段AB旋转后扫过的面积,解答B要求我们熟练操作计算器.