中考数学二次函数复习题附答案Word文档格式.docx

中考数学二次函数复习题附答案Word文档格式.docx

《中考数学二次函数复习题附答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《中考数学二次函数复习题附答案Word文档格式.docx（16页珍藏版）》请在冰豆网上搜索。

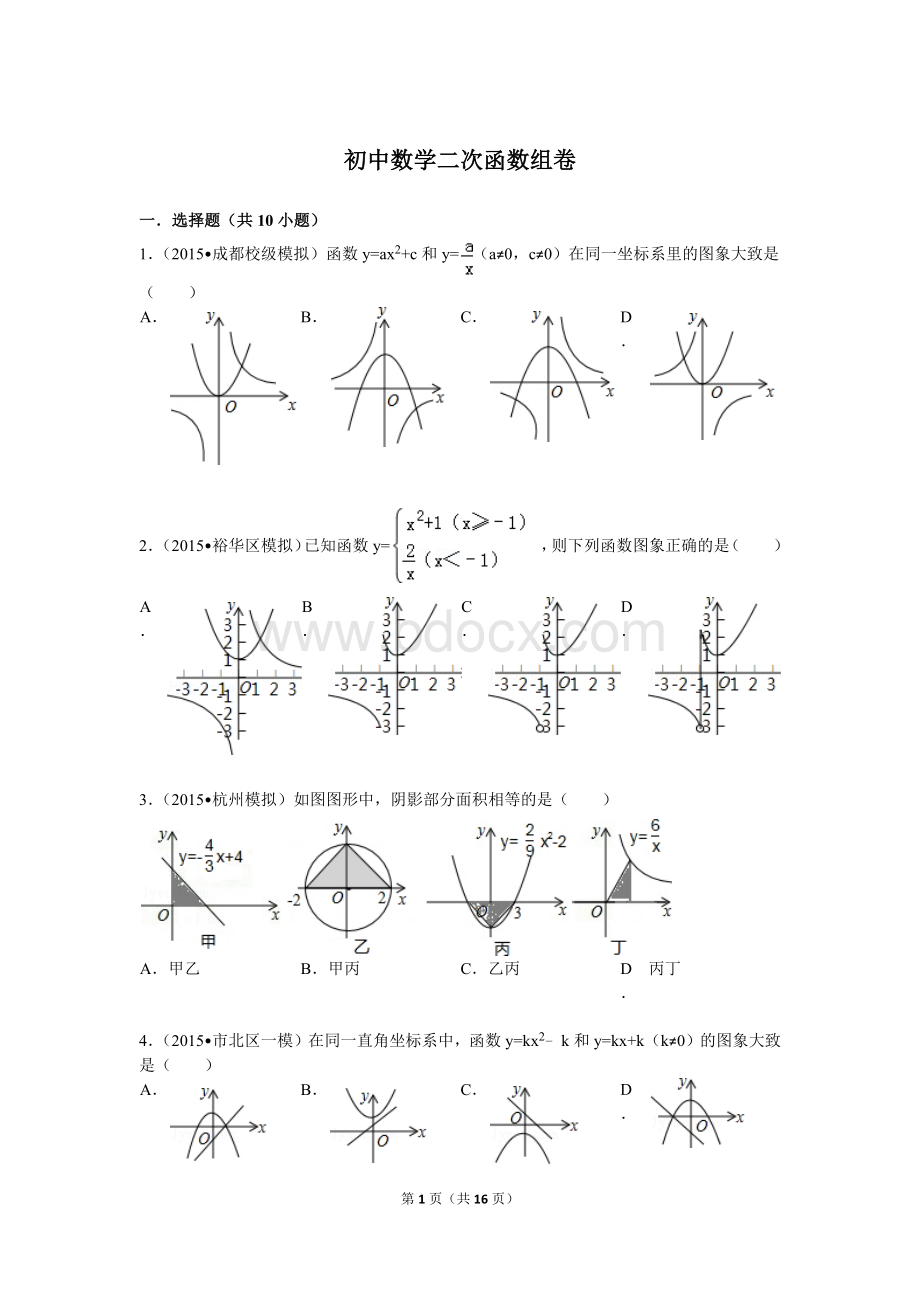
4．（2015•市北区一模）在同一直角坐标系中，函数y=kx2﹣k和y=kx+k（k≠0）的图象大致是（　　）

5．（2015•苏州一模）二次函数y=（x﹣2）2+1的图象的顶点坐标是（　　）

（2，1）

（﹣2，1）

（2，﹣1）

（﹣2，﹣1）

6．（2015•黄陂区校级模拟）二次函数y=x2的图象的开口方向是（　　）

向上

向下

向左

向右

7．（2015•山西模拟）抛物线y=﹣x2不具有的性质是（　　）

开口向上

对称轴是y轴

在对称轴的左侧，y随x的增大而增大

最高点是原点

8．（2015•徐汇区一模）已知二次函数y=ax2﹣2x+2（a＞0），那么它的图象一定不经过（　　）

第一象限

第二象限

第三象限

第四象限

9．（2015•莒县一模）如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：

①abc＞0；

②ax2+bx+c=0的两根分别为﹣3和1；

③b＞2a；

④﹣2b+c＜0；

其中正确的命题是（　　）

①②

②④

①③

③④

10．（2015•崇明县一模）如果二次函数y=ax2+bx+c的图象如图所示，那么下列判断中，不正确的是（　　）

a＞0

b＞0

c＜0

b2﹣4ac＞0

二．填空题（共15小题）

11．（2015•青浦区一模）如果抛物线y=（a+3）x2﹣5不经过第一象限，那么a的取值范围是　　　　　　．

12．（2015•盐城校级模拟）若抛物线y=x2﹣kx+k﹣1的顶点在x轴上，则k=　　　　　　．

13．（2015•徐汇区一模）二次函数y=x2﹣4x﹣5的图象的对称轴是直线　　　　　　．

14．（2015•温州模拟）已知二次函数，若y随x的增大而减小，则x的取值范围是　　　　　　．

15．（2015•河西区一模）抛物线y=﹣2x2+x﹣4的对称轴为　　　　　　．

16．（2015•高新区一模）函数y=﹣（x+1）2+5的最大值为　　　　　　．

17．（2015•大庆校级模拟）用配方法把二次函数y=2x2+3x+1写成y=a（x+m）2+k的形式　　　　　　．

18．（2015春•张掖校级月考）二次函数y=3（x﹣1）2+2图象的顶点坐标为　　　　　　．

19．（2014•路桥区模拟）如图，如果反比例函数的图象经过抛物线y=﹣x2﹣2x的顶点，那么这个反比例函数的解析式为　　　　　　．

20．（2014•杨浦区一模）函数y=（x+5）（2﹣x）图象的开口方向是　　　　　　．

21．（2015春•锦州校级月考）二次函数y=x2﹣6x+3k的图象与x轴有两个交点，则k的取值范围是　　　　　　．

22．（2013•本溪）在平面直角坐标系中，把抛物线y=﹣x2+1向上平移3个单位，再向左平移1个单位，则所得抛物线的解析式是　　　　　　．

23．（2012•上海）将抛物线y=x2+x向下平移2个单位，所得抛物线的表达式是　　　　　　．

24．（2011•黑龙江）抛物线y=﹣（x+1）2﹣1的顶点坐标为　　　　　　．

25．（2010•黔东南州）二次函数y=（x+1）2﹣1，当1＜y＜2时，x的取值范围是　　　　　　．

三．解答题（共5小题）

26．（2015•福建模拟）求二次函数y=﹣2（x﹣3）2﹣5的顶点坐标．

27．（2015•齐齐哈尔模拟）如图，二次函数y=x2+bx+c的图象经过坐标原点，且与x轴交于A（﹣2，0）．

（1）求此二次函数解析式及顶点B的坐标；

（2）在抛物线上有一点P，满足S△AOP=3，直接写出点P的坐标．

28．（2015•嘉定区一模）已知二次函数y=mx2﹣2x+n（m≠0）的图象经过点（2，﹣1）和（﹣1，2），求这个二次函数的解析式，并求出它的图象的顶点坐标和对称轴．

29．（2015•宝山区一模）已知一个二次函数的图象经过点A（1，0）和点B（0，6），C（4，6），求这个抛物线的表达式以及该抛物线的顶点坐标．

30．（2015•岳池县模拟）已知抛物线的顶点坐标是（8，9），且过点（0，1），求该抛物线的解析式．

参考答案与试题解析

考点：

二次函数的图象；

反比例函数的图象．菁优网版权所有

分析：

本题可先由二次函数图象得到字母系数的正负，再与反比例函数的图象相比较看是否一致．逐一排除．

解答：

解：

由A，D中的二次函数图象可得a＞0，c=0，因为y=（a≠0，c≠0），故A，D错误；

由B，C中的二次函数图象可得a＜0，c＞0，所以y=（a≠0，c≠0）的图象在二，四象限内，故C错误，B正确．

故选：

点评：

此题主要考查了反比例函数图象与二次函数图象，应该识记反比例函数在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：

开口方向、对称轴等．

分析y=x2+1在x≥﹣1时的性质和y=在x＜﹣1时的性质，选出正确选项即可．

y=x2+1，开口向上，对称轴是y轴，顶点坐标是（0，1），当x≥﹣1时，B、C、D正确；

y=，图象在第一、三象限，当x＜﹣1时，C正确．

本题考查的是二次函数图象和反比例函数图象，正确理解图象与系数之间的关系是解题的关键．

一次函数的图象；

专题：

数形结合．

甲、丙：

根据函数解析式求出图象与x轴，y轴的交点坐标，再计算阴影部分的面积；

乙：

可判断出阴影部分为斜边为4的等腰直角三角形，据此计算阴影部分的面积；

丁：

利用反比例函数系数k的几何意义求出阴影部分的面积．

甲：

直线y=﹣x+4与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×

3×

4=6；

阴影部分为斜边为4的等腰直角三角形，其面积为×

4×

2=4；

丙：

抛物线y=﹣2与x轴的两个交点为（﹣3，0）与（3，0），顶点坐标为（0，﹣2），则阴影部分的面积为×

6×

2=6；

此函数是反比例函数，那么阴影部分的面积为×

6=3；

因此甲、丙的面积相等，

故选B．

此题主要考查了函数图象与坐标轴交点坐标的求法以及图形面积的求法，是基础题，熟练掌握各类函数的图象特点是解决问题的关键．

一次函数的图象．菁优网版权所有

可先根据一次函数的图象判断k的符号，再判断二次函数图象与实际是否相符，判断正误．

A、由一次函数y=kx+k的图象可得：

k＞0，此时二次函数y=kx2﹣kx的图象应该开口向上，错误；

B、由一次函数y=kx+k图象可知，k＞0，此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴，错误；

C、由一次函数y=kx+k可知，y随x增大而减小时，直线与y轴交于负半轴，错误；

D、正确．

本题考查的是一次函数和二次函数的图象，应该熟记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：

开口方向、对称轴、顶点坐标．

二次函数的性质．菁优网版权所有

根据顶点式的意义直接解答即可．

二次函数y=（x﹣2）2+1的图象的顶点坐标是（2，1）．

故选A．

本题考查了二次函数的性质，要熟悉顶点式的意义，并明确：

y=a（x﹣h）2+k（a≠0）的顶点坐标为（h，k）．

由抛物线解析式可知，二次项系数a=1＞0，可知抛物线开口向上．

∵二次函数y=x2的二次项系数a=1＞0，

∴抛物线开口向上．

本题考查了抛物线的开口方向与二次项系数符号的关系．当a＞0时，抛物线开口向上，当a＜0时，抛物线开口向下．

此题应从二次函数的基本形式入手，它符合y=ax2的基本形式，根据它的性质，进行解答．

因为a＜0，所以开口向下，顶点坐标（0，0），对称轴是y轴，有最高点是原点．

A

此题主要考查y=ax2形式二次函数的基本性质，比较基础，但也是中考中热点问题．

先根据题意判断出二次函数的对称轴方程，再令x=0求出y的值，进而可得出结论．

∵二次函数y=ax2﹣2x+2（a＞0）的对称轴为直线x=﹣=﹣=＞0，

∴其顶点坐标在第一或四象限，

∵当x=0时，y=2，

∴抛物线一定经过第二象限，

∴此函数的图象一定不经过第三象限．

故选C．

本题考查的是二次函数的性质，熟知二次函数的对称轴方程是解答此题的关键．

9．（2015•莒县一模）如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列