南京市重点中学中考一模数学试题及答案Word下载.docx

南京市重点中学中考一模数学试题及答案Word下载.docx

《南京市重点中学中考一模数学试题及答案Word下载.docx》由会员分享，可在线阅读，更多相关《南京市重点中学中考一模数学试题及答案Word下载.docx（14页珍藏版）》请在冰豆网上搜索。

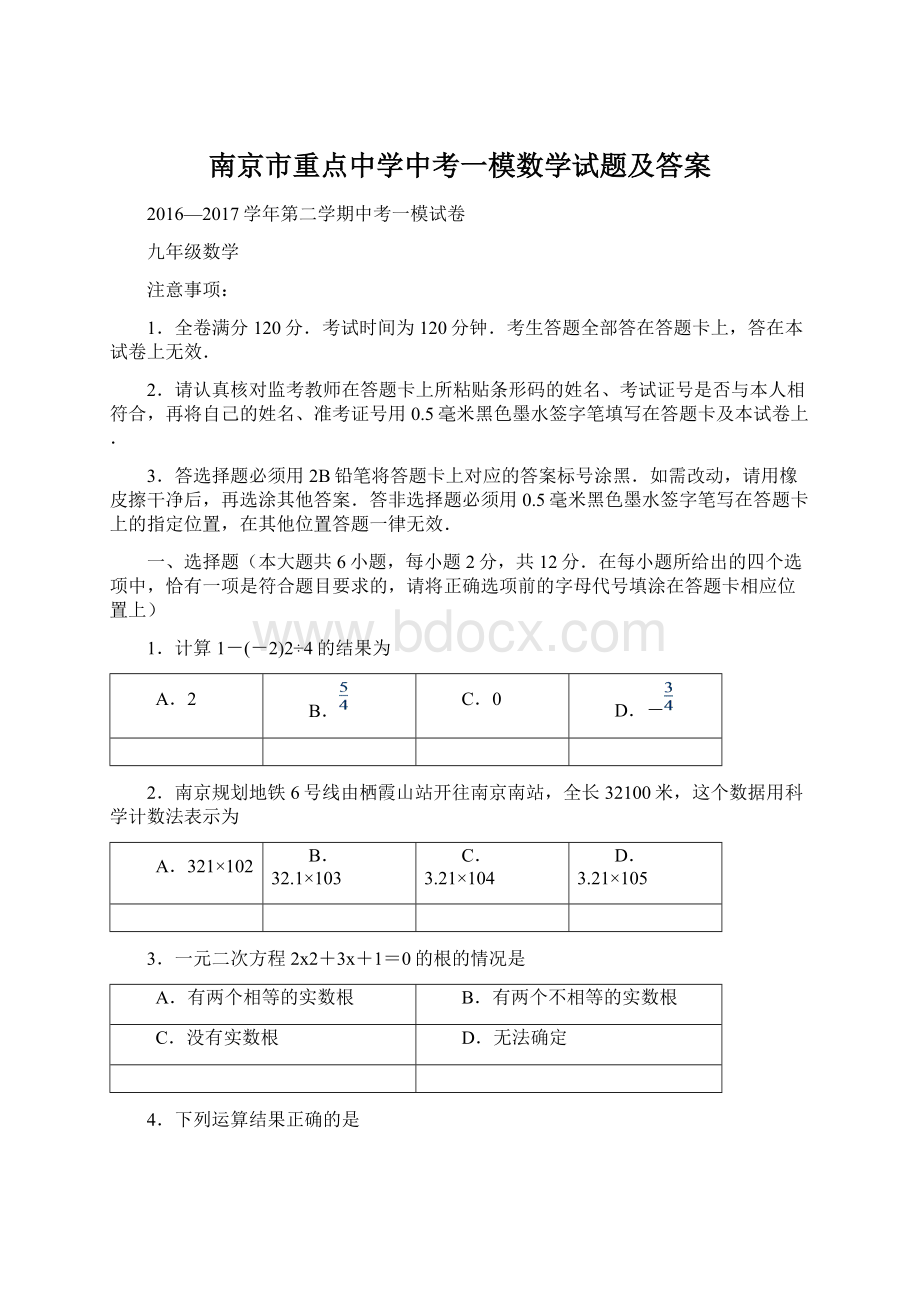
A．有两个相等的实数根

B．有两个不相等的实数根

C．没有实数根

D．无法确定

4．下列运算结果正确的是

A．a2＋a3＝a5　

B．a2·

a3＝a6

C．a3÷

a2＝a

D．（a2）3＝a5

5．如图，将矩形ABCD绕点A逆时针旋转90°

至矩形AEFG，点D的旋转路径为，若AB＝1，BC＝2，则阴影部分的面积为

A．＋

B．1＋

C．

D．＋1

6．如图，将正六边形ABCDEF放入平面直角坐标系后，若点A、B、E的坐标分别为

（a，b）、（3，1）、（－a，b），则点D的坐标为

A．（1，3）

B．（3，－1）

C．（－1，－3）

D．（－3，1）

二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

7．分解因式2x2＋4x＋2＝▲．

8．满足不等式组的整数解为▲．

9．已知一组数据2，6，5，2，4，则这组数据的中位数是▲．

10．计算＝▲．

11．若关于x的方程x2＋mx＋5＝0有一个根为1，则该方程的另一根为▲．

12．如图，△ABC是⊙O的内接三角形，AD是⊙O直径，若∠ABC＝50°

，

则∠CAD＝▲°

．

13．如图，在□ABCD中，E、F分别是AD、CD的中点，EF与BD相交于点M，若△DEM的面积为1，则□ABCD的面积为▲．

14．如图，A（a，b）、B（1，4）（a＞1）是反比例函数y＝（x＞0）图像上两点，过A、B分别作x轴、y轴的垂线，垂足分别为C、D、E、F，AE、BD交于点G．则四边形ACDG的面积随着a的增大而▲．（填“减小”、“不变”或“增大”）

15．二次函数y＝a（x－b）2＋c（a＜0）的图像经过点（1，1）和（3，3），则b的取值范围是▲．

16．如图，在△ABC中，∠C＝90°

，AC＝BC＝1，P为△ABC内一个动点，∠PAB＝∠PBC，则CP的最小值为▲．

三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

17．（10分）

（1）解方程组

（2）解方程＝．

18．（6分）计算÷

19．（7分）一个不透明的袋子中，装有2个红球，1个白球，1个黄球，这些球除颜色外都相同．求下列事件的概率：

（1）搅匀后从中任意摸出1个球，恰好是红球；

（2）搅匀后从中任意摸出2个球，2个都是红球．

20．（8分）某公司在某市五个区投放共享单车供市民使用，投放量的分布及投放后的使用情况统计如下．

（1）该公司在全市一共投放了▲万辆共享单车；

（2）在扇形统计图中，B区所对应扇形的圆心角为▲°

；

（3）该公司在全市投放的共享单车的使用量占投放量的85%，请计算C区共享单车的使用量并补全条形统计图．

21．（8分）如图，在□ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE＝CG，AH＝CF，且EG平分∠HEF．

（1）求证：

△AEH≌△CGF；

（2）求证：

四边形EFGH是菱形．

22．（7分）用两种方法证明“直角三角形斜边上的中线等于斜边的一半”．

已知：

如图，在Rt△ABC中，∠ACB＝90°

，CD是斜边AB上的中线．

求证：

CD＝AB．

证法1：

如图，在∠ACB的内部作∠BCE＝∠B，

CE与AB相交于点E．

∵∠BCE＝∠B，

∴①▲．

∵∠BCE＋∠ACE＝90°

∴∠B＋∠ACE＝90°

又∵②▲，

∴∠ACE＝∠A．

∴EA＝EC．

∴EA＝EB＝EC，

即CE是斜边AB上的中线，且CE＝AB．

又∵CD是斜边AB上的中线，即CD与CE重合，

∴CD＝AB．

请把证法1补充完整，并用不同的方法完成证法2．

23．（9分）同时点燃甲乙两根蜡烛，蜡烛燃烧剩下的长度y（cm）与燃烧时间x（min）的关系如图所示．

（1）求乙蜡烛剩下的长度y与燃烧时间x的函数表达式；

（2）求点P的坐标，并说明其实际意义；

（3）求点燃多长时间，甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍．

24．（8分）定义：

在△ABC中，∠C＝30°

，我们把∠A的对边与∠C的对边的比叫做∠A的邻弦，记作thiA，即thiA＝＝．请解答下列问题：

已知：

（1）若∠A＝45°

，求thiA的值；

（2）若thiA＝，则∠A＝▲°

（3）若∠A是锐角，探究thiA与sinA的数量关系．

25．（8分）A厂一月份产值为16万元，因管理不善，二、三月份产值的月平均下降率为x（0＜x＜1）．B厂一月份产值为12万元，二月份产值下降率为x，经过技术革新，三月份产值增长，增长率为2x．三月份A、B两厂产值分别为yA、yB（单位：

万元）．

（1）分别写出yA、yB与x的函数表达式；

（2）当yA＝yB时，求x的值；

（3）当x为何值时，三月份A、B两厂产值的差距最大？

最大值是多少万元？

26．（8分）如图，在Rt△ABC中，∠A＝90°

，点D、E分别在AC、BC上，且CD·

BC＝AC·

CE，以E为圆心，DE长为半径作圆，⊙E经过点B，与AB、BC分别交于点F、G．

AC是⊙E的切线；

（2）若AF＝4，CG＝5，

①求⊙E的半径；

②若Rt△ABC的内切圆圆心为I，则IE＝▲．

27．（9分）在△ABC中，D为BC边上一点．

（1）如图①，在Rt△ABC中，∠C＝90°

，将△ABC沿着AD折叠，点C落在AB边上．请用直尺和圆规作出点D（不写作法，保留作图痕迹）；

（2）如图②，将△ABC沿着过点D的直线折叠，点C落在AB边上的E处．

①若DE⊥AB，垂足为E，请用直尺和圆规作出点D（不写作法，保留作图痕迹）；

②若AB＝4，BC＝6，∠B＝45°

，则CD的取值范围是▲．

数学试题参考答案及评分标准

说明：

本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．

一、选择题（本大题共6小题，每小题2分，共12分）

题号

1

2

3

4

5

6

答案

C

B

A

D

二、填空题（本大题共10小题，每小题2分，共20分）

7．2（x＋1）28．－29．410．2－11．5

12．4013．1614．增大15．b＞216．－1

三、解答题（本大题共11小题，共88分）

17．（本题10分）

（1）解方程组:

解：

由得y＝2x—1

将代入得：

x+2（2x－1）＝3

x＝1………2分

将x＝1代入得y＝1………4分

∴该方程组的解为：

……5分

（2）方程两边同乘（x－1）（x＋3）得：

x＋3＝2（x－1）………2分

解得x＝5………4分

检验：

当x＝5时，（x－1）（x＋3）≠0

所以x＝5是原方程的解……5分

18．（本题6分）

÷

＝÷

＝·

＝．……6分

19.（本题7分）

（1）解：

搅匀后从中任意摸出1个球，所有可能出现的结果共有4种，它们出现的可能性相同．所有的结果中，满足“恰好是红球”（记为事件A）的结果有2种，

所以P（A）＝＝．……3分

（2）解：

搅匀后从中任意摸出2个球，所有可能出现的结果有：

（红1，红2）、（红1，黄）、（红2，黄）、（红1，白）、（红2，白）、（白，黄），共有6种，它们出现的可能性相同．所有的结果中，满足“2个都是红球”（记为事件B）的结果只有1种，所以P（B）＝．……7分

20．（本题8分）

（1）4……2分

（2）36……4分

（3）图略4×

85%－0.8－0.3－0.9－0.7＝0.7（万辆）

答：

C区共享单车的使用量为0.7万辆．……8分

21．（本题8分）

证明：

（1）∵四边形ABCD是平行四边形，

∴∠A＝∠C．

又∵AE＝CG，AH＝CF，

∴△AEH≌△CGF．……3分

（2）∵四边形ABCD是平行四边形，

∴AD＝BC，AB＝CD，∠B＝∠D．

∵AE＝CG，AH＝CF，

∴EB＝DG，HD＝BF．

∴△BEF≌△DGH．

∴EF＝HG．

又∵△AEH≌△CGF，

∴EH＝GF．

∴四边形HEFG为平行四边形．……5分

∴EH∥FG，

∴∠HEG＝∠FGE．

∵EG平分∠HEF，

∴∠HEG＝∠FEG，

∴∠FGE＝∠FEG，

∴EF＝GF，

∴EFGH是菱形．……8分

22．（本题7分）①EC＝EB；

②∠A＋∠B＝90°

……2分

证法2：

延长CD至点E，使得DE＝CD，连接AE、BE．

∵AD＝DB，DE＝CD．

∴四边形ACBE是平行四边形．

又∵∠ACB＝90°

∴□ACBE是矩形．

∴AB＝CE，

又∵CD＝CE

∴CD＝AB……7分

23．（本题9分）

（1）设y与x之间的函数表达式为y＝kx＋b．

根据题意，当x＝0时，y＝40；

当x＝50时，y＝0．

所以，解得．

所以，y与x之间的函数表达式为y＝－0.8x＋40．……3分

（2）P（20，24）点燃20分钟，甲乙两根蜡烛剩下的长度都是24cm．……5分

（3）设甲蜡烛剩下的长度y甲与x之间的函数表达式为y甲＝mx＋n．

根据题意，当x＝0时，y甲＝48；

当x＝20时，y甲＝24．

所以，解得．所以，y甲与x之间的函数表达式为y甲＝－1.2x＋48．

因为甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍，

所以－1.2x＋48＝1.1（－0.8x＋40）

解得x＝12.5

点燃12.5分钟，甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍．……9分

24．（本题8分）

（1）如图，作BH⊥AC，垂足为H．

在Rt△BHC中，sinC＝＝，即BC＝2BH．

在Rt△BHA中，sinA＝＝，即AB＝BH．

∴thiA＝＝．……3分

（2）60或120．……5分

（3）在Rt△ABC中，thiA＝．

在Rt△BHA中，sinA＝．

∴thiA＝2sinA．……8分

25．（本题8分）