应用时间序列分析第4章答案.docx
《应用时间序列分析第4章答案.docx》由会员分享,可在线阅读,更多相关《应用时间序列分析第4章答案.docx(12页珍藏版)》请在冰豆网上搜索。
河南大学:
姓名:
汪宝班级:
七班学号:
1122314451班级序号:
68
5:
我国1949年-2008年年末人口总数(单位:
万人)序列如表4-8所示(行数据).选择适当的模型拟合该序列的长期数据,并作5期预测。
解:
具体解题过程如下:
(本题代码我是做一问写一问的)
1:
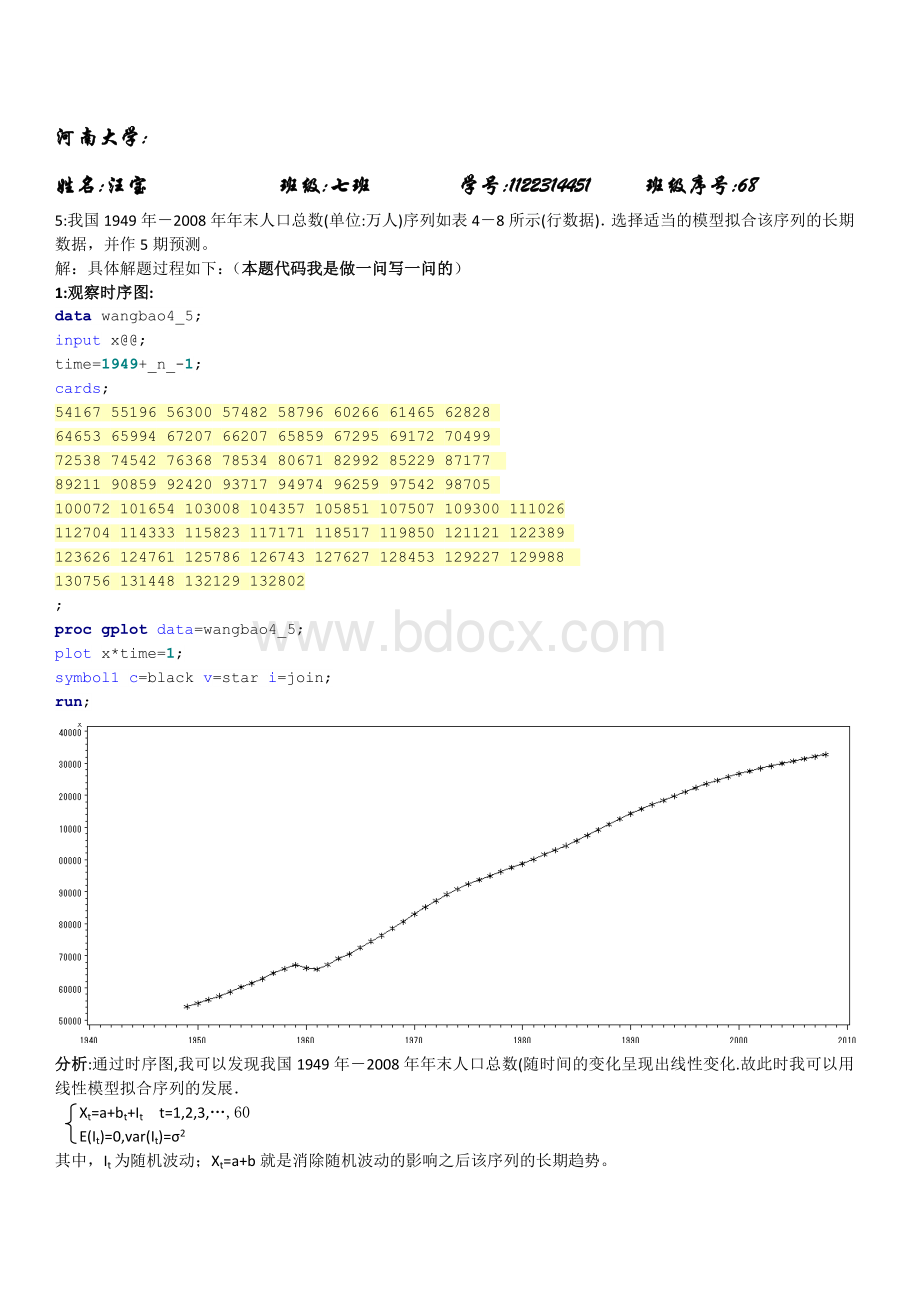
观察时序图:
datawangbao4_5;
inputx@@;
time=1949+_n_-1;
cards;
5416755196563005748258796602666146562828
6465365994672076620765859672956917270499
7253874542763687853480671829928522987177
8921190859924209371794974962599754298705
100072101654103008104357105851107507109300111026
112704114333115823117171118517119850121121122389
123626124761125786126743127627128453129227129988
130756131448132129132802
;
procgplotdata=wangbao4_5;
plotx*time=1;
symbol1c=blackv=stari=join;
run;
分析:
通过时序图,我可以发现我国1949年-2008年年末人口总数(随时间的变化呈现出线性变化.故此时我可以用线性模型拟合序列的发展.
Xt=a+bt+Itt=1,2,3,…,60
E(It)=0,var(It)=σ2
其中,It为随机波动;Xt=a+b就是消除随机波动的影响之后该序列的长期趋势。
2:
进行线性模型拟合:
procautoregdata=wangbao4_5;
modelx=time;
outputout=outp=wangbao4_5_cup;
run;
procgplotdata=out;
plotx*time=1wangbao4_5_cup*time=2/overlay;
symbol2c=redv=nonei=joinw=2l=3;
run;
分析:
由上面输出结果可知:
两个参数的p值明显小于0.05,即这两个参数都是具有显著非零,
4:
模型检验
又因为RegressR-square=totalR-square=0.9931,即拟合度达到99.31%所以用这个模型拟合的非常好。
5:
结论
所以本题拟合的模型为:
Xt=-2770828+1449t+Itt=1,2,3,…,60
E(It)=0,var(It)=σ2
6:
作5期预测
procforecastdata=wangbao4_5method=stepartrend=2lead=5
out=outoutfulloutest=est;
idt;
varx;
procgplotdata=out;
plotx*time=_type_/href=2008;
symbol1i=nonev=starc=black;
symbol2i=joinv=nonec=red;
symbol3i=joinv=nonec=blackl=2;
symbol4i=joinv=nonec=blackl=2;
run;
6:
爱荷华州1948-1979年非农产品季度收入数据如表4——9所示(行数据),选择适当的模型拟合该序列的长期趋势。
解:
具体做题过程如下:
(本题代码我是做一问写一问的)
1、绘制时序图
datawangbao4_6;
inputx@@;
time=_n_;
cards;
601604620626641642645655682678692707
736753763775775783794813823826829831
830838854872882903919937927962975995
100110131021102810271048107010951113114311541173
117811831205120812091223123812451258127812941314
132313361355137714161430145514801514154515891634
166917151760181218091828187118921946198320132045
204820972140217122082272231123492362244224792528
257126342684279028902964308531593237335834893588
362437193821393440284129420543494463459847254827
49395067523154085492565358285965
;
procgplotdata=wangbao4_6;
plotx*time;
symbolc=blackv=stari=join;
run;
分析;可知时序图显示该序列有明显的曲线递增趋势。
尝试使用修正指数型模型进行迭代拟合:
+Єt,t=1,2,…,128
2、拟合模型
procnlinmethod=gauss;
modelx=a+b*c**time;
parametersa=0.1b=0.1c=1.1;
outputpredicted=xhatout=out;
run;
NLIN过程输出以下六方面信息:
(1)迭代过程
(2)收敛状况
(本次迭代收敛)
(3)估计信息摘要
(4)主要统计量
(5)参数信息摘要
得到的拟合模型为:
t=1,2,…,128
(6)近似相关矩阵
3、拟合效果
为了直观看出拟合效果,我们可以将原序列值和拟合值联合作图:
procgplotdata=out;
plotx*t=1xhat*t=2/overlay;
symbol1c=blackv=stari=join;
symbol2c=redv=nonei=join;
分析:
由上图图我们可以看出,原序列值和拟合值很接近,拟合效果较好。
综合以上的分析,我们可以选择模型:
来拟合该序列的长期趋势。
拟合效果很不错。
8:
某城市1980年1月至1995年8月每月屠宰生猪的数量(单位:
头)如表4—11所示(行数据),选择适当的模型拟合该序列的发展,并预测1995年9月至1997年9月该城市的生猪屠宰量。
解:
具体解题过程如下:
(本题代码我是做一问写一问的)
atawangbao4_8;
inputx@@;
time=_n_;
cards;
763787194733873964281050849574111064710031194133103055
905951014577688981291916439622810273610026410349197027
9524091680101259109564768928577395210937719820297906
100306940891026807791993561117062812258835710617591922
1041141099599788010538696479975801094901101919097498981
1071889417711509711369611453212011093607110925103312120184
103069103351111331106161111590994471019878533386970100561
89543892658271979498748467381977029784468697875878
69571757226418277357632925938078332723815597169750
85472701337912585805817788685269069795568817466698
72258734457613186082754437396978139786466626973776
80034706948182375640755408222975345770347858979769
75982780747758884100979668905193503847477453191900
816358979781022782657727185043954187956810328395770
912971012441145251011399386695171100183103926102643108387
97077909019033688732837599926773292789439439992937
9013091055106062103560104075101783937911023138241383534
10901196499102430103002918159906711006710159997646104930
88905899361067238430711489610674987892100506
;
procgplotdata=wangbao4_8;
plotx*time=1;
symbol1c=redi=joinv=star;
run;
procarimadata=wangbao4_8;
identifyvar=x;
run;
1:
时序图与平稳性判别
分析:
上图是数据对应的时序图,从图上曲线分析来看,数据并没有周期性或者趋向性规律,并且每月的生猪的屠宰量大约在80000上下波动。
所以由该序列图我可以认为它是个平稳的数列。
即可以用第三章的AR模型或MA模型或ARMA模型进行拟合。
但是为了稳妥起见,我还需要利用自相关图进一步辅助识别。
具体如下:
自相关图:
分析:
由上图可知:
样本自相关图中的自相关系数在延迟4阶之后几乎全部落入2个标准差范围之内,并且向零衰减的速度还是比较快的。
所以我认为该序列是平稳的序列。
由时序图与自相关图可知其是平稳序列。
故可以用第三章的AR模型或MA模型或ARMA模型进行拟合
分析:
由上面数据可知:
由于p值显著小于0.05,故可以否定原假设(H0),接受备选假设(H1),即我可以认为该序列是平稳的非纯随机性序列。
这样就说明了我们可以根据历史信息预测未来月的生猪屠宰量。
分析:
观察自相关图和偏自相关图,从这两图来看,偏自