高中数学 41 坐标系 413 球坐标系与柱坐标系课后训练 苏教版选修44Word文档下载推荐.docx

高中数学 41 坐标系 413 球坐标系与柱坐标系课后训练 苏教版选修44Word文档下载推荐.docx

《高中数学 41 坐标系 413 球坐标系与柱坐标系课后训练 苏教版选修44Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《高中数学 41 坐标系 413 球坐标系与柱坐标系课后训练 苏教版选修44Word文档下载推荐.docx（64页珍藏版）》请在冰豆网上搜索。

∴，

.

∴

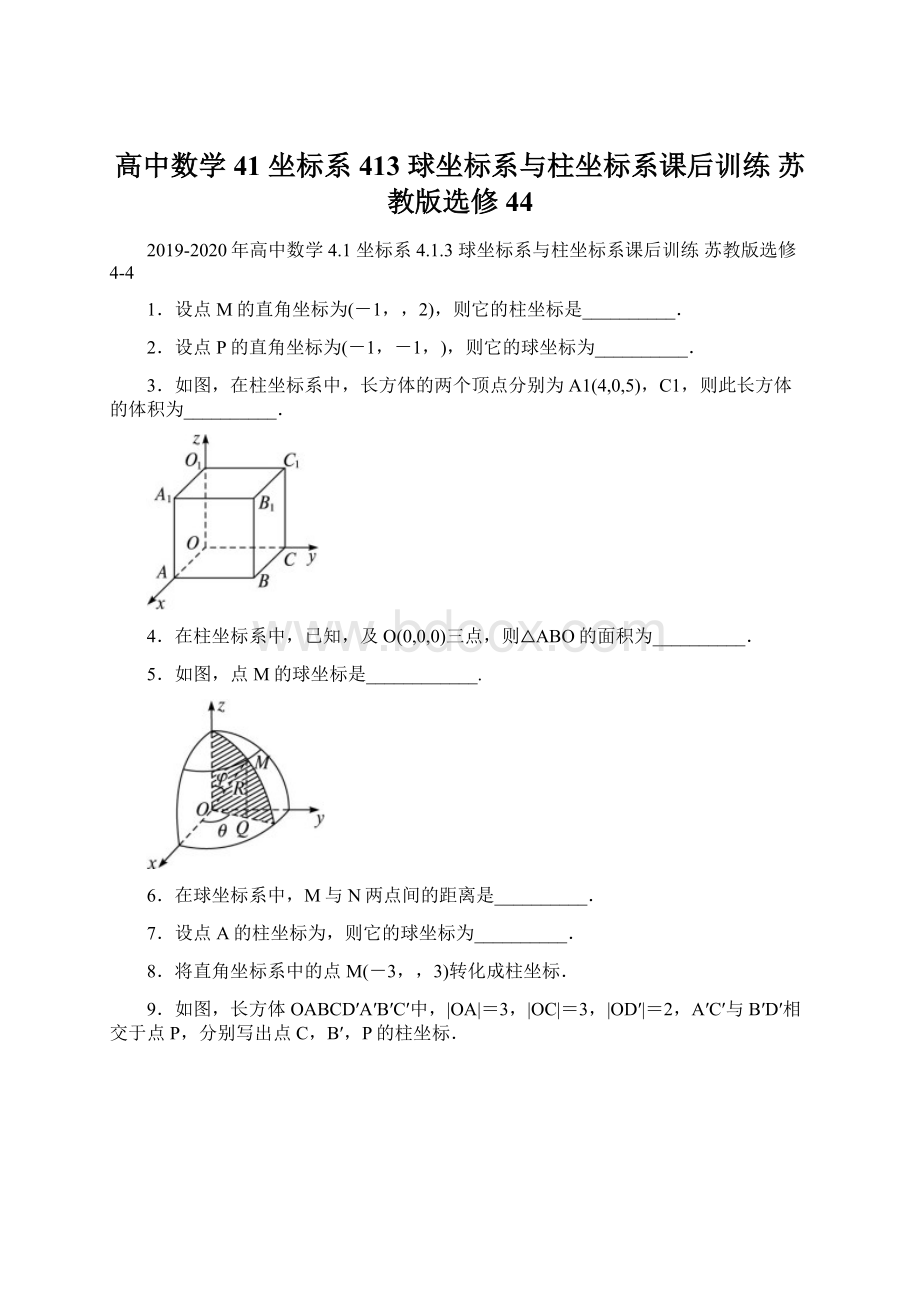
∵0≤φ≤π，∴.

∴P点的球坐标为.

3.答案：

120

由长方体的两个顶点分别为A1（4,0,5），C1，可知|OA|＝4，|OC|＝6，|OO1|＝5，

故长方体的体积为4×

5×

6＝120.

4.答案：

1

∵，，O（0,0,0），

∴△OAB为直角三角形．

5.答案：

（R，φ，θ）

抓住球坐标定义，记|OM|＝R，OM与z轴正向所夹的角为φ，设M在Oxy平面上的射影为Q，Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.这样点M的位置就可以用有序数组（R，φ，θ）表示．故点M的球坐标为（R，φ，θ）．

6.答案：

4

设点M的直角坐标为（x，y，z），则

∴M点的直角坐标为（，，），

同理，N点的直角坐标为（，，）．

∴|MN|＝

＝4.

7.答案：

设A的直角坐标为（x，y，z），

则，

，，

∴点A的直角坐标为（1,1，）．

设点A的球坐标为（r，φ，θ）．

则有

∴tanθ＝1.又∵0≤θ＜2π，x＞0，

∴.

又∵0≤φ≤π，∴.

∴点A的球坐标为.

8.解：

设点M的柱坐标为（r，θ，z），

则由

得

∵0≤θ＜2π且x＜0，∴，.

∴M点的柱坐标为.

9.解：

∵，|OC|＝3，

∴点C的柱坐标为.

∵，|BB′|＝2，，

∴点B′的柱坐标为.

同理，点P的柱坐标为.

10.解：

建立如图所示的坐标系，过点M作底面xCy的垂线MN交AB于点N.

∵ABC－A1B1C1是直三棱柱，

∴N点在线段AB上．

由点N分别作x轴，y轴的垂线NE，NF，垂足为E，F，

根据已知，可得△ABC是等腰直角三角形，

∴|NE|＝|NF|＝.

故点M的空间直角坐标为.

由于点M在平面xCy上的射影为点N，

|CN|＝，∠ECN＝，

故点M的柱坐标为.

2019-2020年高中数学4.1坐标系教案苏教版选修4-4

4．1.1直角坐标系

课标解读

1.掌握在平面直角坐标系中刻画点的位置的方法，体会坐标系的作用．

2.对具体问题，能建立适当的坐标系，使所刻画的代数形式具有更简便的结果.

1．直线坐标系

在直线上，取一个点为原点，并确定一个长度单位和直线的方向，就建立了直线上的坐标系，即数轴．

数轴上任意一点P都可以由惟一的实数x确定，x称为点P的坐标．

2．平面直角坐标系

在平面上，取两条互相垂直的直线的交点为原点，并确定一个长度单位和这两条直线的方向，就建立了平面直角坐标系．

平面上任意一点P都可以由惟一的有序实数对（x，y）确定，（x，y）称为点P的坐标．

3．空间直角坐标系

在空间中，选择两两垂直且交于一点的三条直线，取这三条直线的交点为原点，并确定一个长度单位和这三条直线的方向，就建立了空间直角坐标系．

空间中任意一点P都可以由惟一的三元有序实数组（x，y，z）确定，（x，y，z）称为点P的坐标．

1．建立适当的坐标系一般有哪些规则？

【提示】　

（1）如果图形有对称中心，可以选择对称中心为坐标原点；

（2）如果图形有对称轴，可以选择对称轴为坐标轴；

（3）使图形上的特殊点尽可能多的落在坐标轴上．

2．由坐标（x，y）怎样确定点的位置？

【提示】　在平面直角坐标系中，分别过点M（x,0），N（0，y）作x轴和y轴的垂线，两条直线的交点P即（x，y）所确定的点.

建立适当的坐标系刻画点的位置

　正方形的边长等于4，试选择适当的坐标系，表示其顶点与中心的坐标．

【自主解答】　　法一　以正方形的一个顶点为原点，两条邻边为坐标轴，且把第四个顶点放在第一象限，建立平面直角坐标系，如图

（1）所示．此时，其四个顶点的坐标分别为O（0,0）、A（4,0）、B（4,4）、C（0,4），中心为M（2,2）．

法二　以正方形的中心为原点，且使两条坐标轴平行于正方形的边，建立平面直角坐标系，如图

（2）所示．此时，正方形的顶点坐标分别为A（2，－2）、B（2,2）、C（－2,2）、D（－2，－2），中心为O（0,0）．

法三　以正方形的两条对角线为坐标轴建立直角坐标系，如图（3）所示．此时，正方形的顶点坐标分别为A（2

，0）、B（0,2

）、C（－2

，0）、D（0，－2

），中心为O（0,0）．（作图时只要以图

（2）中的原点O为圆心，OA为半径作圆，该圆与坐标轴的四个交点即是图（3）中正方形的各个顶点）

选择适当的坐标系，表示两条直角边长都为1的直角三角形的三个顶点的坐标．

【解】　法一　以直角三角形的两条直角边AC、BC所在直线分别为x轴、y轴，建立如图

（1）所示的平面直角坐标系，则C（0,0），A（1,0），B（0,1）．

法二　以斜边AB所在直线为x轴，线段AB的中垂线为y轴，建立如图

（2）所示的平面直角坐标系．则A（－

，0），B（

，0），C（0，

）．

建立坐标系解决证明问题

　用解析法证明：

等腰三角形底边延长线上一点，到两腰的距离之差等于一腰上的高．

【自主解答】　　如图，在△ABC中，AB＝AC，

P为BC延长线上一点，PD⊥AB于D，PE⊥AC于E，CF⊥AB于F，以BC所在直线为x轴，以BC的中垂线为y轴，

建立直角坐标系，如图所示，

设A（0，b），B（－a,0），C（a,0）（a＞0，b＞0），则直线AB的方程为bx－ay＋ab＝0，

直线AC的方程为bx＋ay－ab＝0，

取P（x0,0），使x0＞a，则点P到直线AB、AC的距离分别为

PD＝

＝

，

PE＝

点C到直线AB的距离为

CF＝

则PD－PE＝

＝CF.

故所需证明命题成立．

已知△ABC中，AB＝AC，BD、CE分别为两腰上的高，求证：

BD＝CE.

【证明】　如图，以BC所在直线为x轴，BC的垂直平分线为y轴建立平面直角坐标系．

设B（－a,0），C（a,0），A（0，h）．

则直线AC的方程为y＝－

x＋h，

即：

hx＋ay－ah＝0.

直线AB的方程为y＝

hx－ay＋ah＝0.

由点到直线的距离公式得：

BD＝

CE＝

∴BD＝CE.

建立坐标系求轨迹方程

　如图4－1－1所示，过点P（2,4）有两条互相垂直的直线l1，l2，l1交x轴于A点，l2交y轴于B点，求线段AB的中点M满足的方程．

图4－1－1

【思路探究】　法一　设点→求斜率→斜率积为－1→整理得方程→检查有无不适合的点→结论

法二　设M（x，y）→寻求M满足的条件→列方程→检查有无不适合的点→结论

法三：

O，A，P，B四点共圆→PM＝MO→求kOP及OP中点坐标→点斜式写出OP的垂直平分线方程为所求

【自主解答】　法一　设点M的坐标为（x，y），因为M为线段AB的中点，所以点A的坐标为（2x,0），点B的坐标为（0,2y）．

因为l1⊥l2，且l1，l2过点P（2,4），

所以kAP·

kPB＝－1.

而kAP＝

（x≠1），kPB＝

，所以

·

＝－1（x≠1），整理，得x＋2y－5＝0（x≠1）．

因为当x＝1时，点A，B的坐标分别为（2,0），（0,4），所以线段AB的中点坐标是（1,2），它满足方程x＋2y－5＝0.

综上所述，点M满足的方程是x＋2y－5＝0.

法二　设点M的坐标为（x，y），则A，B两点的坐标分别是（2x,0），（0,2y），

连接PM.因为l1⊥l2，所以PM＝

AB.

而PM＝

AB＝

所以2

化简，得x＋2y－5＝0，即为所求方程．

法三　因为l1⊥l2，OA⊥OB，点M为线段AB的中点，所以O，A，P，B四点共圆，

且该圆的圆心为M（x，y），所以PM＝MO，所以点M的轨迹为线段OP的垂直平分线．

因为kOP＝

＝2，OP的中点坐标为（1,2），所以点M满足的方程为y－2＝－

（x－1），

化简得x＋2y－5＝0.

通过建立坐标系精确地刻画集合图形的位置和物体运动的轨迹的方法称为解析法．解决此类问题的关键：

（1）建立平面直角坐标系；

（2）设点（点与坐标的对应）；

（3）列式（方程与坐标的对应，列出几何条件，并将几何条件代数化）；

（4）化简（注意变形的等价性）；

（5）证明（若保证等价变形，则此步骤可以省略）．

设圆（x－1）2＋y2＝1的圆心为C，过原点作圆的弦OA，求OA中点B的轨迹方程．

【解】　法一　（直接法）：

设B点坐标为（x，y），

由题意，得OB2＋BC2＝OC2，如图所示，

即x2＋y2＋[（x－1）2＋y2]＝1，即OA中点B的轨迹方程为（x－

）2＋y2＝

（去掉原点）．

法二　（几何法）：

由题意知CB⊥OA，OC的中点记为M（

，0），

则MB＝

OC＝

故B点的轨迹方程为（x－

法三　（代入法）：

设A点坐标为（x1，y1），B点坐标为（x，y），

由题意得

即

又因为（x1－1）2＋y

＝1，

所以（2x－1）2＋（2y）2＝1，

即（x－

法四　（交点法）：

设直线OA的方程为y＝kx，

当k＝0时，B为（1,0）；

当k≠0时，直线BC的方程为：

y＝－

（x－1），直线OA，BC的方程联立消去k即得其交点轨迹方程：

y2＋x（x－1）＝0，即（x－

（x≠0,1），

显然B（1,0）满足（x－

故（x－

（去掉原点）为所求．

　（教材第16页习题4.1第4题）据气象台预报，在A市正东方300km的B处有一台风中心形成，并以每小时40km的速度向西北方向移动，在距台风中心250km以内的地区将受其影响．问：

从现在起经过多少时间，台风将影响A市，持续时间多长？

　（xx·

郑州模拟）已知B村位于A村的正西方向1公里处，原计划经过B村沿着北偏东60°

的方向埋设一条地下管线m.但在A村的西北