北京中考一模几何综合汇总.doc
《北京中考一模几何综合汇总.doc》由会员分享,可在线阅读,更多相关《北京中考一模几何综合汇总.doc(9页珍藏版)》请在冰豆网上搜索。
几何综合
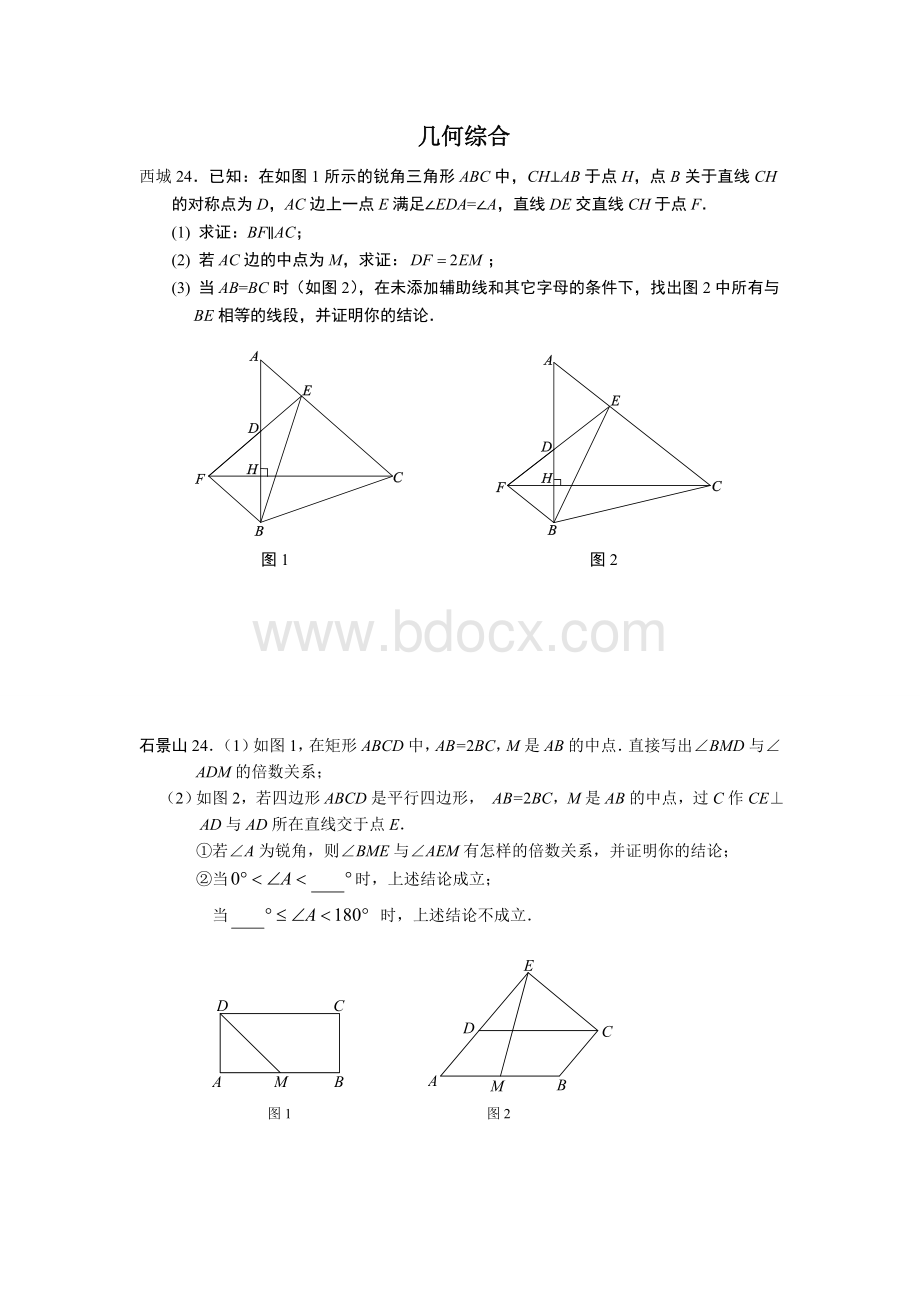
西城24.已知:
在如图1所示的锐角三角形ABC中,CH⊥AB于点H,点B关于直线CH的对称点为D,AC边上一点E满足∠EDA=∠A,直线DE交直线CH于点F.
(1)求证:
BF∥AC;
(2)若AC边的中点为M,求证:
;
(3)当AB=BC时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE相等的线段,并证明你的结论.
图1图2
石景山24.
(1)如图1,在矩形ABCD中,AB=2BC,M是AB的中点.直接写出∠BMD与∠ADM的倍数关系;
(2)如图2,若四边形ABCD是平行四边形,AB=2BC,M是AB的中点,过C作CE⊥AD与AD所在直线交于点E.
①若∠A为锐角,则∠BME与∠AEM有怎样的倍数关系,并证明你的结论;
②当时,上述结论成立;
当时,上述结论不成立.
图1图2
平谷25.两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,
∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:
AF+EF=DE;
(2)若将图①中的绕点B按顺时针方向旋转角,且,其它条件不变,请在图②中画出变换后的图形,并直接写出⑴中的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角,且,其它条件不变,如图③.你认为⑴中的结论还成立吗?
若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
解:
(1)证明:
(2)结论:
AF+EF=DE.(填成立还是不成立)
门头沟24.已知:
在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.
(1)如图l,当∠ACB=90°时,直接写出线段DE、CE之间的数量关系;
(2)如图2,当∠ACB=120°时,求证:
DE=3CE;
(3)如图3,在
(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG关于直线DG对称(点B的对称点是点K),延长DK交AB于点H.若BH=10,求CE的长.
丰台24.已知:
△ABC和△ADE是两个不全等的等腰直角三角形,其中BA=BC,DA=DE,联结EC,取EC的中点M,联结BM和DM.
(1)如图1,如果点D、E分别在边AC、AB上,那么BM、DM的数量关系与位置关系是;
(2)将图1中的△ADE绕点A旋转到图2的位置时,判断
(1)中的结论是否仍然成立,并说明理由.
房山25.如图1,在△ABC中,∠ACB=90°,AC=BC=,以点B为圆心,以为半径作圆.
⑴设点P为☉B上的一个动点,线段CP绕着点C顺时针旋转90°,得到线段CD,联结DA,DB,PB,如图2.求证:
AD=BP;
⑵在⑴的条件下,若∠CPB=135°,则BD=___________;
⑶在⑴的条件下,当∠PBC=_______°时,BD有最大值,且最大值为__________;
当∠PBC=_________°时,BD有最小值,且最小值为__________.
昌平25.如图,在四边形ABCD中,对角线AC、BD相交于点O,直线MN经过点O,设锐角∠DOC=∠,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线AD’、BC’相交于点P.
(1)当四边形ABCD是矩形时,如图1,请猜想AD’、BC’的数量关系以及∠APB与∠α的大小关系;
(2)当四边形ABCD是平行四边形时,如图2,
(1)中的结论还成立吗?
(3)当四边形ABCD是等腰梯形时,如图3,∠APB与∠α有怎样的等量关系?
请证明.
顺义25.问题:
如图1,在Rt△中,,,点是射线CB上任意一点,△ADE是等边三角形,且点D在的内部,连接BE.探究线段BE与DE之间的数量关系.
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
(1)当点D与点C重合时(如图2),请你补全图形.由的度数为,点E落在,容易得出BE与DE之间的数量关系为;
(2)当点D在如图3的位置时,请你画出图形,研究线段BE与DE之间的数量关系是否与
(1)中的结论相同,写出你的猜想并加以证明.
延庆图1
24.如图1,已知:
已知:
等边△ABC,点D是边BC上一点(点D不与点B、点C重合),
求证:
BD+DC>AD
下面的证法供你参考:
把绕点A瞬时间针旋转得到,连接ED,
则有,DC=EB
∵AD=AE,
∴是等边三角形
∴AD=DE
在中,BD+EB>DE
即:
BD+DC>AD
实践探索:
(1)请你仿照上面的思路,探索解决下面的问题:
图3
如图2,点D是等腰直角三角形△ABC边上的点(点D不与B、C重合),
求证:
BD+DC>AD
图2
(2)如果点D运动到等腰直角三角形△ABC外或内时,BD、DC和AD之间又存在怎样的数量关系?
直接写出结论.
创新应用:
(3)已知:
如图3,等腰△ABC中,AB=AC,且∠BAC=(为钝角),D是等腰△ABC外一点,且∠BDC+∠BAC=180º,BD、DC与AD之间存在怎样的数量关系?
写出你的猜想,并证明.
海淀
24.在□ABCD中,∠A=∠DBC,过点D作DE=DF,且∠EDF=∠ABD,连接EF、EC,
N、P分别为EC、BC的中点,连接NP.
(1)如图1,若点E在DP上,EF与DC交于点M,试探究线段NP与线段NM的数量
关系及∠ABD与∠MNP满足的等量关系,请直接写出你的结论;
(2)如图2,若点M在线段EF上,当点M在何位置时,你在
(1)中得到的结论仍然
成立,写出你确定的点M的位置,并证明
(1)中的结论.
M
B
D
C
F
E
A
N
P
P
N
A
E
F
C
D
B
图1图2
密云
24.已知:
正方形中,,绕点顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)如图1,当绕点旋转到时,有.当绕点旋转到时,如图2,请问图1中的结论还是否成立?
如果成立,请给予证明,如果不成立,请说明理由;
(2)当绕点旋转到如图3的位置时,线段和之间有怎样的等量关系?
请写出你的猜想,并证明.
通州BC
AD
25.已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C
两点重合),线段BE的垂直平分线交射线AC于点P,联结DP,PE.
(1)若四边形ABCD是正方形,猜想PD与PE的关系,
并证明你的结论.
AD
BC
(2)若四边形ABCD是矩形,
(1)中的PD与PE的关系还成立吗?
(填:
成立或不成立).
(3)若四边形ABCD是矩形,AB=6,cos∠ACD=,
设AP=x,△PCE的面积为y,当AP>AC时,求y与x之间的函数关系式.
东城24.已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.
(1)如图1,若AB=,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);
(2)如图2,当点P为射线BC上任意一点时,猜想EF与图中的哪条线段相等(不能添加辅助线产生新的线段),并加以证明;
(3)若AB=,设BP=,以QF为边的等边三角形的面积y,求y关于的函数关系式.
朝阳25.在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从
(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:
①∠PEF的大小是否发生变化?
请说明理由;
②直接写出从开始到停止,线段EF的中点所经过的路线长.