中考专题复习圆的极值.doc

中考专题复习圆的极值.doc

《中考专题复习圆的极值.doc》由会员分享，可在线阅读，更多相关《中考专题复习圆的极值.doc（6页珍藏版）》请在冰豆网上搜索。

中考数学专题复习：

圆

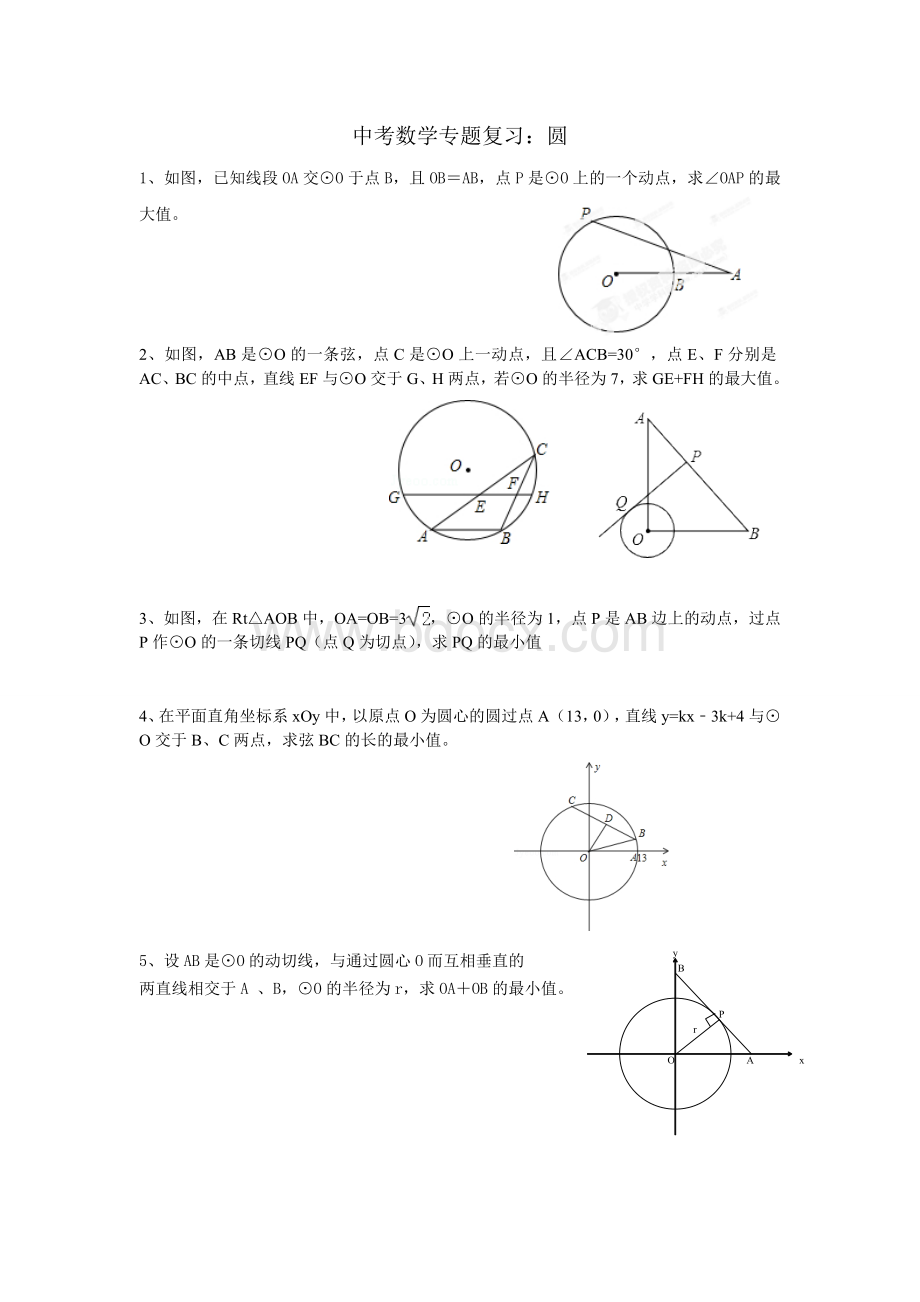
1、如图，已知线段OA交⊙O于点B，且OB＝AB，点P是⊙O上的一个动点，求∠OAP的最大值。

2、如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为7，求GE+FH的最大值。

3、如图，在Rt△AOB中，OA=OB=3，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），求PQ的最小值

4、在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O交于B、C两点，求弦BC的长的最小值。

5、设AB是⊙O的动切线，与通过圆心O而互相垂直的

两直线相交于A、B，⊙O的半径为r，求OA＋OB的最小值。

6、如图，圆O与正方形ABCD的两边AB、AD相切，E与圆O上一点．若圆O的半径为4，且AB=7，求DE的最大值

7、如图6，中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，求线段PQ长度的最小值

8、如图，在⊙O上有定点C和动点P，位于直径AB的异侧，过点C作CP的垂线，与PB的延长线交于点Q，已知：

⊙O半径为，tan∠ABC=，求CQ的最大值

9、在平面直角坐标系xOy中，已知点A（6，0），

点B（0，6），动点C在以半径为3的⊙O上，连接

OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．AC，BC，当点C在⊙O上运动时，求出△ABC的面积的最大值．

10、如图，已知，⊙O的直径CD为4，点A在⊙O上，∠ACD=30°，B为弧AD的中点，P为直径CD上一动点，求BP+AP的最小值

11、如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，求线段EF长度的最小值

12、在平面直角坐标系中，点A的坐标为（3.0），点B为y轴正半轴上的一点，点C是第一象限内一点，且AC=2．设tan∠BOC=m，求m的最小值．

13、如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，求PM长度的最大值

14、如图，已知直角△AOB中，直角顶点O在单位圆心上，斜边与单位圆相切，延长AO，BO分别与单位圆交于C，D．试求四边形ABCD面积的最小值．

15、如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以O为圆心OA长为半径作⊙O，C为半圆弧AB上的一个动点（不与A、B两点重合），射线AC交⊙O于点E，BC=，AC=，求的最大值.

16、如图，∠BAC=60°，半径长为1的圆O与∠BAC的两边相切，P为圆O上一动点，以P为圆心，PA长为半径的圆P交射线AB、AC于D、E两点，连接DE，求线段DE长度的最大值

17.（2012山东烟台）如图，⊙O1,⊙O,⊙O2的半

径均为2cm,⊙O3,⊙O4的半径均为1cm，⊙O与

其他4个圆均相外切，图形既关于O1O2所在直

线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为（）

A.12cm2B.24cm2

C.36cm2D.48cm2

18.如图，在Rt△ABC中，∠C=90°，AC=6,BC=8,

⊙O为△ABC的内切圆，点D是斜边AB的中点，

则tan∠ODA的值为（）

18如图1，Rt△ABC中，∠ACB=90°，AB=5，BC=3，点D在边AB的延长线上，BD=3，过点D作DE⊥AB，与边AC的延长线相交于点E，以DE为直径作⊙O交AE于点F．

（1）求⊙O的半径及圆心O到弦EF的距离；

（2）连接CD，交⊙O于点G（如图2）．求证：

点G是CD的中点．

19如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．

（1）求线段EC的长；

（2）求图中阴影部分的面积．

20如图,△ABC中，∠ACB=90°,D是边AB上一点，且∠A=2∠DCB.E是BC边上的一点，以EC为直径的⊙O经过点D.

（1）求证：

AB是⊙O的切线；

（2）若CD的弦心距为1，BE=EO，求BD的长.

21如图所示，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E.

（1）求证：

∠BCA=∠BAD；

（2）求DE的长；

（3）求证：

BE是⊙O的切线.

22如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=

30°,

（1）求∠COB的度数；

（2）求⊙O的半径R；

（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合.在EF的同一侧，这样的三角形共有多少个？

你能在其中找出另一个顶点在⊙O上的三角形吗？

请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比.

23、已知如图，过O且半径为5的⊙P交x的正半轴于点M（2m，0）、交y轴的负半轴于点D，弧OBM与弧OAM关于x轴对称，其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点.

（1）当m=4时，

①填空：

B的坐标为，C的坐标为，D的坐标为；

②若以B为顶点且过D的抛物线交⊙P与点E，求此抛物线的函数关系式和写出点E的坐标；

③除D点外，直线AD与②中的抛物线有无其它公共点？

并说明理由．

（2）是否存在实数m，使得以B、C、D、E为顶点的四边形组成菱形？

若存在，求m的值；若不存在，请说明理由.

24、如图，在RTABC中，C=90（A>B）。

它的两个锐角正弦值恰为方程的两根。

他的内切圆半径为，抛物线过A、B、C三点

（1）.求m的值

（2）.求抛物线的解析式

（3）.在抛物线上是否存在点P,使=8,若存在，求出P的坐标，若不存在说明理由

如图，直线y=－x+1与两轴分别交于A、B两点，以AB为边长在第一象限内作正三角形ABC.圆为ABC的外接圆与x轴交于另一点E

（1）.求C点坐标

（2）.求过C点与AB中点的直线的解析式

（3）.求过点E、、A三点的二次函数的解析式