初中数学《最值问题》典型例题 完整版Word文档格式.docx

初中数学《最值问题》典型例题 完整版Word文档格式.docx

《初中数学《最值问题》典型例题 完整版Word文档格式.docx》由会员分享，可在线阅读，更多相关《初中数学《最值问题》典型例题 完整版Word文档格式.docx（8页珍藏版）》请在冰豆网上搜索。

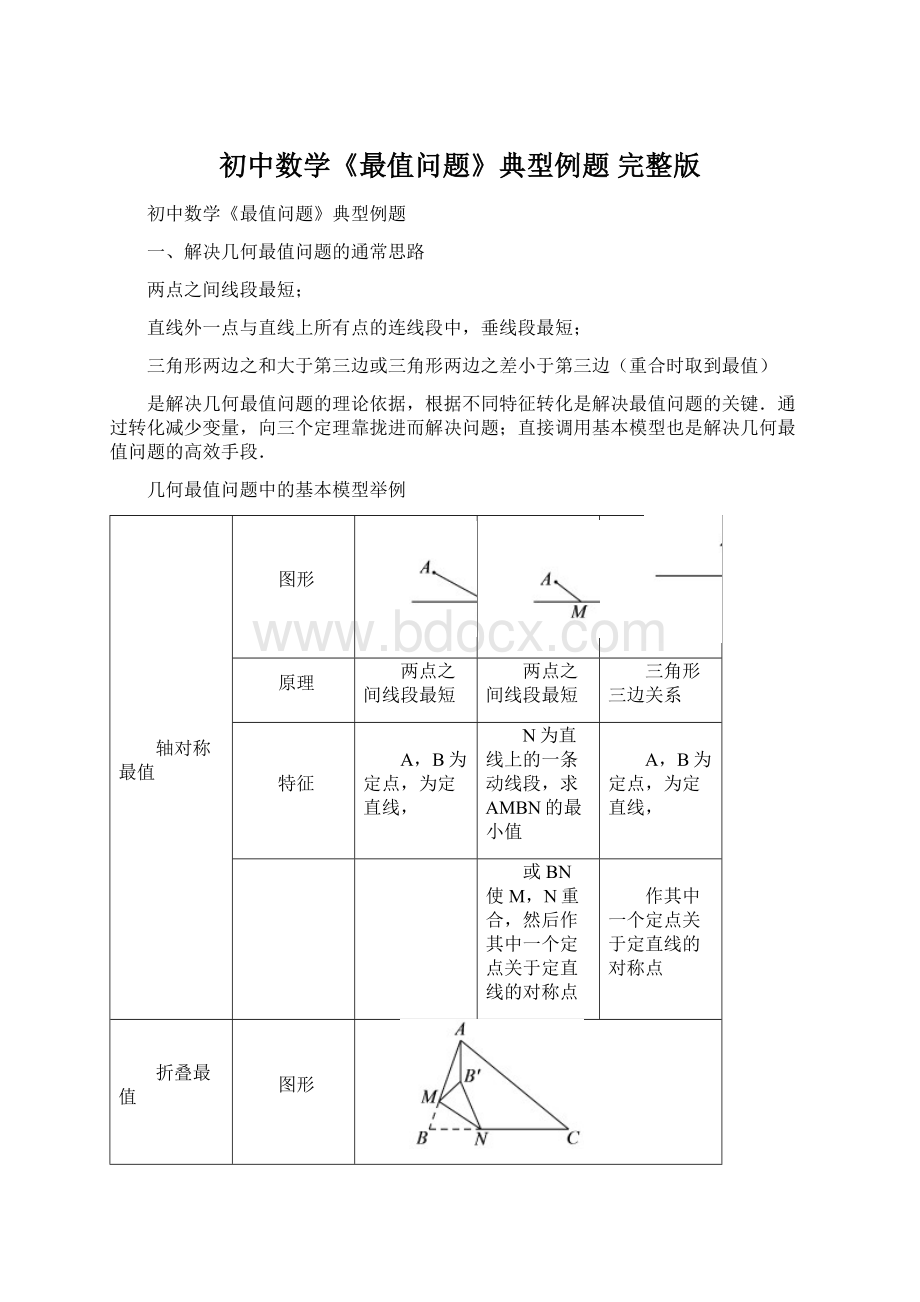
图形

原理

两点之间线段最短

三角形三边关系

特征

A，B为定点，为定直线，

N为直线上的一条动线段，求AMBN的最小值

或BN使M，N重合，然后作其中一个定点关于定直线的对称点

作其中一个定点关于定直线的对称点

折叠最值

在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'

，连接AB'

，求AB'

的最小值．

转化

转化成求AB'

B'

NNC的最小值

二、典型题型

1．如图：

点、N分别在边OA、OB上运动，若∠AOB=45°

，ON的周长的最小值为　　．

【分析】作，N是CD与OA，OB的交点时，△，N是CD与OA，OB的交点时，△N周长最小的条件是解题的关键．

2．如图，当四边形=4，点B到直线的距离BN=1，且MN=4，的值然后根据勾股定理求得，

利用勾股定理求出AB′=5

∴|ON=90°

，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为　　．

【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．

【解答】解：

如图，取AB的中点E，连接OD、OE、DE，

∵∠MON=90°

，AB=2

∴OE=AE=AB=1，

∵BC=1，四边形ABCD是矩形，

∴AD=BC=1，

∴DE=，

根据三角形的三边关系，OD＜OEDE，

∴当OD过点E是最大，最大值为1．

故答案为：

1．

【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．

7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE，那么DE长的最小值是　　．

【分析】设AC=，BC=4﹣，根据等腰直角三角形性质，得出CD=，CD′=（4﹣），根据勾股定理然后用配方法即可求解．

设AC=，BC=4﹣，

∵△ABC，△BCD′均为等腰直角三角形，

∴CD=，CD′=（4﹣），

∵∠ACD=45°

，∠BCD′=45°

，

∴∠DCE=90°

∴DE2=CD2CE2=2（4﹣）2=2﹣48=（﹣2）24，

∵根据二次函数的最值，

∴当取2时，DE取最小值，最小值为：

4．

2．

【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．

8．如图，菱形ABCD中，AB=2，∠A=120°

，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PKQK的最小值为　　　　　　．

【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PKQK的最小值，然后求解即可．

如图，∵AB=2，∠A=120°

∴点P′到CD的距离为2×

=，

∴PKQK的最小值为．

．

【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．

9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′CC′DD′的取值范围是　．

【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：

S△ADP=S正方形ABCD=，S△ABPS△ACP=S△ABC=S正方形ABCD=，继而可得AP•（BB′CC′DD′）=1，又由1≤AP≤，即可求得答案．

连接AC，DP．

∵四边形ABCD是正方形，正方形ABCD的边长为1，

∴AB=CD，S正方形ABCD=1，

∵S△ADP=S正方形ABCD=，S△ABPS△ACP=S△ABC=S正方形ABCD=，

∴S△ADPS△ABPS△ACP=1，

∴AP•BB′AP•CC′AP•DD′=AP•（BB′CC′DD′）=1，

则BB′CC′DD′=，

∵1≤AP≤，

∴当P与B重合时，有最大值2；

当P与C重合时，有最小值．

∴≤BB′CC′DD′≤2．

≤BB′CC′DD′≤2．

【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADPS△ABPS△ACP=1，继而得到BB′CC′DD′=．

10．如图，菱形ABCD中，∠A=60°

，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PEPF的最小值是　　．

【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PEPF的最小值，进而求出即可．

由题意可得出：

当P与D重合时，E点在AD上，F在BD上，此时PEPF最小，

连接BD，

∵菱形ABCD中，∠A=60°

∴AB=AD，则△ABD是等边三角形，

∴BD=AB=AD=3，

∵⊙A、⊙B的半径分别为2和1，

∴PE=1，DF=2，

∴PEPF的最小值是3．

3．

【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．