小学六年级数学知识点总复习Word文档格式.docx

小学六年级数学知识点总复习Word文档格式.docx

《小学六年级数学知识点总复习Word文档格式.docx》由会员分享，可在线阅读，更多相关《小学六年级数学知识点总复习Word文档格式.docx（14页珍藏版）》请在冰豆网上搜索。

2、十进制计数法：

每相邻的两个计数单位之间的进率都是十。

3、数位：

在计数时，计数单位要按照一定的顺序排列起来，它们所在的位置叫做数位。

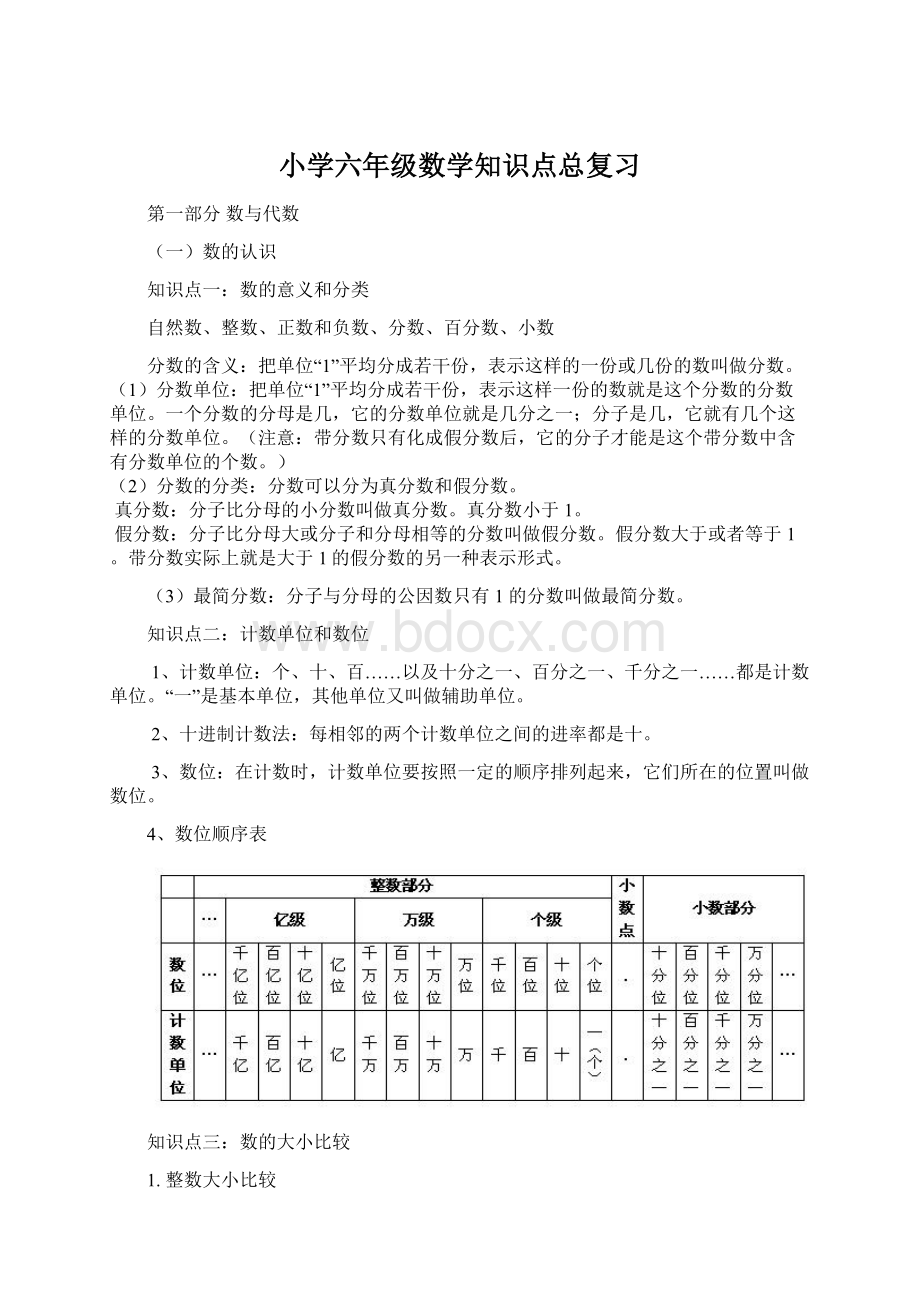
4、数位顺序表

知识点三：

数的大小比较

1.整数大小比较

① 

位数多的整数大于位数少的整数。

如七位数大于六位数。

② 

位数相同，从高位到低位依次进行比较，最高位大的数较

大；

如果最高位相同，再比较左起第二位，第二位大的数较大，依此类推。

2.小数大小比较

先看整数部分（按整数大小比较）,整数部分大的小数比较大;

如果整数部分相同,就看十分位,十分位大的小数比较大…….

3.分数大小比较

（1）真假分数或整数部分相同的带分数：

分母相同，分子大则分数大；

分子相同，则分母小的分数大；

分子和分母都不相同，通分后化成同分母的分数再比较大小。

（2）整数部分不同的带分数，整数部分大的则分数大。

知识点四：

数的性质

1、分数的基本性质：

分数的分子和分母同时乘或者除以相同的数（0除外），分数的大小不变。

2、小数的基本性质：

小数的末尾添上0或者去掉0，小数的大小不变。

3、小数点位置移动引起小数大小变化的规律

知识点五：

数的改写与近似数

1.把数改写成以“万”或“亿”为单位的数

对于一个比较大的整数来说，为了便于读写方便，往往可以把它改写成用“万”或“亿”作单位的数。

具体方法是：

（1）把一个数改写成用“万”作单位的数。

将该数的小数点向左移动四位，再在后面加上“万”字。

如43000=4.3万。

（2）把一个数改写成用“亿”作单位的数。

将该数的小数点向左移动八位，再在后面加上“亿”字。

如576000000=5.76亿。

注意：

改写应得到准确值，所以用等号。

2.取近似数的几种方法：

（1）四舍五入法：

看要保留的那一位后面一位，如果后面一位的数字大于或等于5，就去掉这一位和它后面所有的数，再向前进1，得到要求的近似数；

如果要保留的那一位后面一位的数字小于或等于4，就去掉这一位和它后面所有的数，从而得到要求的近似数。

例：

求下列各数的近似数

3.54963≈3.5（保留到十分位）3.54963≈3.55（保留百分位）

3.54963≈3.550（保留到千分位）注意,3.550末尾的0为什么不能去掉？

（2）去尾法：

根据需要，不管要保留数位后面是多少，都将它去掉，这种取近似数的方法叫做“去尾法”。

（3）进一法：

根据实际需要，不管保留的数位后面是多少，都要向前进一，这种取近似数的方法叫做进一法。

小数、分数、百分数的互化

互化

方法

小数化成分数

原来有几位小数，就在1后面写几个0作分母，把原来小数去掉小数点作分子。

能约分的要约成最简分数。

小数化成百分数

把小数点向右移动两位（位数不够用0补足）,同时在后面添上百分号.

百分数化成小数

把百分号去掉,同时把小数点向左移动两位（位数不够用0补足）.

分数化成百分数

先把分数化成小数,（遇到除不尽时,通常要求保留三位小数）,再化成百分数.

百分数化成分数

先把百分数改写成分母是100的分数,能化简的要化简;

因数、倍数、质数、合数

1、因数和倍数

已知a、b、c均为正整数，且a×

b=c,那么c就是a和b的倍数，a和b就是c的因数。

倍数和因数是相互依存的。

一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它的本身；

一个数的倍数的个数是无限的，其中最小的倍数是它本身，没有最大的倍数。

一个数既是它自身的因数，又是它自身的倍数。

2、最大公因数和最小公倍数

最大公因数：

几个数公有的因数，叫做这几个数的公因数，其中最大的一个，叫做这几个数的最大公因数。

最小公倍数：

几个数公有的倍数，叫做这几个数的公倍数，其中最小的一个，叫做这几个数的最小公倍数。

3、质数和合数

质数：

一个数，如果只有1和它本身两个因数，这样的数叫做质数

最小的质数是2。

合数：

一个数，如果除了1和它本身两个因数外还有别的因数，这样的数叫做合数。

最小的合数是4。

1既不是质数，也不是合数。

（二）数的运算

四则运算的意义

1、加法的意义：

把两个数合并成一个数的运算。

2、减法的意义：

已知两个数的和与其中的一个加数，求另一个加数的运算。

3、整数乘法的意义：

求几个相同加数的和的简便运算。

4、小数乘法的意义：

小数乘整数与整数乘法的意义相同，也是求几个相同加数的和的简便运算；

一个数乘小数求这个数的十分之几、百分之几……是多少。

5、分数乘法的意义：

分数乘整数与整数乘法的意义相同，也是求几个相同加数的和的简便运算；

一个数乘分数就是求这个数的几分之几是多少。

6、除法的意义：

已知两个因数的积和其中的一个因数，求另一个因数的运算。

四则运算的法则

整数加减法，小数加减法，分数加减法，整数乘法，分数乘法，整数除法，小数除法，分数除法

四则混合运算

加法和减法叫做第一级运算，乘法和除法叫做第二级运算。

在一个没有括号的算式里，如果只含有同一级运算，要从左往右依次计算；

如果含有两级运算，要先做第二级运算，再做第一级运算。

在一个有括号的算式里，要先算小括号里面，再算中括号里面的，最后算大括号里面的。

运用定律，使计算简便

加法交换律：

a+b=b+a加法结合律：

（a+b）+c=a+（b+c）

乘法交换律：

ab=ba乘法结合律：

（ab）c=a（bc）乘法分配律：

a（b+c）=ab+ac

除法的性质：

a÷

b÷

c=a÷

c÷

b=a÷

（b×

c）

减法的性质：

a-b-c=a-c-b=a-（b+c）

通过运算解决问题

（三）式与方程

用字母表示数、运算定律和计算公式

方程和等式

1、等式：

表示相等关系的式子叫等式。

2、方程：

含有未知数的等式叫方程。

3、等式和方程的关系：

所有的方程都是等式，但等式不一定是方程。

4、方程的解：

使方程左右两边相等的未知数的值，叫方程的解。

5、解方程：

求方程的解的过程，叫解方程。

列方程解应用题的一般步骤

1、弄清题意，找出未知数并用x表示。

2、找出题中数量间的相等关系，并根据等量关系列出方程。

3、解方程，求出未知数的值。

4、检验并作答。

（四）常见的量

知识点：

常见的计量单位及其进率

1、长度单位：

常见长度单位：

千米（km）米（m）分米（dm）厘米（cm）毫米（mm）

1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米

2、面积单位：

常见的面积单位：

平方千米（km²

）公顷（hm²

）平方米（m²

）平方分米（dm²

）平方厘米（cm²

1平方千米=100公顷1公顷=10000平方米

1平方米=100平方分米1平方分米=100平方厘米

3、体积单位：

常见的体积单位：

立方米（m³

）立方分米（dm³

）立方厘米（cm³

）升（L）毫升（ml）

1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1立方毫米

1升=1000毫升1立方分米=1升1立方厘米=1毫升

4、质量单位：

常见的质量单位：

吨（t）千克（kg）克（g）

1吨=1000千克1千克=1000克

5、时间单位：

常见的时间单位：

世纪年月日时分秒

不能被4整除的年份叫做平年。

能被4整除的年份叫做闰年。

（公历年份是整百数的，必须是400的倍数才是闰年）。

1世纪=100年1年=12个月1天=24小时1小时=60分1分=60秒

28天（平年二月）

1个月=29天（闰年二月）

30天（四、六、九、十一月）

31天（一、三、五、七、八、十、十二月）

1天=24小时1小时=60分1分=60秒

6、人民币的单位：

常用的人民币：

元角分1元=10角1角=10分

名数的改写：

高级单位的名数化成低级单位的名数乘以进率，低级单位的名数化成高级单位的名数除以进率。

（五）比和比例

比和比例的联系与区别

比

比例

意义

两数相除又叫两个数的比

表示两个比相等的式子叫做比例

各部分名称

0.8:

0.4=2

前项比号后项比值

2：

3=6：

9

外项内项内项外项

基本性质

比的前项和后项都乘上或除以相同的数（0除外），比值不变

在比例中，两外项之积等于两内项之积

化简比的依据

解比例的依据

（四）、比例尺

一幅图的比例尺是指图上距离和实际距离的比。

比例尺有数值比例尺和线段比例尺。

正比例和反比例的意义和判断方法

1.正比例的意义2.反比例的意义3.判断正反比例的方法

一找二看三判断

（1）找变量：

分析数量关系，确定那两种量是相关联的量

（2）看定量：

分析这两种相关联的量，它们之间的关系是商一定，还是积一定。

（3）判断：

如果商一定，就是正比例；

如果积一定，就成反比例；

如果商或积都不是定量，就不成比例。

第二部分空间与图形

（一）图形的认识与测量

平面图形的认识

1、直线、射线和线段

（1）联系与区别

名称

特点

线段

直线上两点间的一段叫做线段。

线段有两个端点，它可以度量长度。

射线

把线段的一端无限延长，就得到一条射线。

射线只有一个端点，它是无限长的，不能度量长度。

直线

把线段的两端无限延长，就可以得到一条直线。

直线没有端点，它是无限长的，不能度量长度。

（2）垂直于平行

a、垂直和垂线：

两条直线相交成直角时，这两条直线互相垂直。

其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

b、平行线：

在同一平面内，不相交的两条直线叫做平行线。

两条平行线之间的距离相等。

同一平面内的两条直线不是平行，就是相交。

c、点到直线的距离：

从直线外的一点向该直线引垂线，从这点到垂足的线段的长，叫做这个点到直线的距离。

2、角的认识

（1）角的意义：

从一点引出的两条射线所组成的图形叫做角。

角的大小与边的长短无关，与两边叉开的大小有关。

（2）角的分类：

锐角：

小于90°

的角

直角：

等于90°

角钝角：

大于90°

而小于180°

平角：

等于180°

周角：

等于360°

3、三角形

（1）三角形的意义：

三角形是由三条线段首尾相接围城的图形。

（2）三角形的特性：

三角形具有稳定性。

（3）三角形的分类：

锐角三角形：

三个角都是锐角的三角形

三角形

按角分直角三角形：

有一个角是直角的三角形