二次函数图像与性质专题复习题文档格式.doc

二次函数图像与性质专题复习题文档格式.doc

《二次函数图像与性质专题复习题文档格式.doc》由会员分享，可在线阅读，更多相关《二次函数图像与性质专题复习题文档格式.doc（11页珍藏版）》请在冰豆网上搜索。

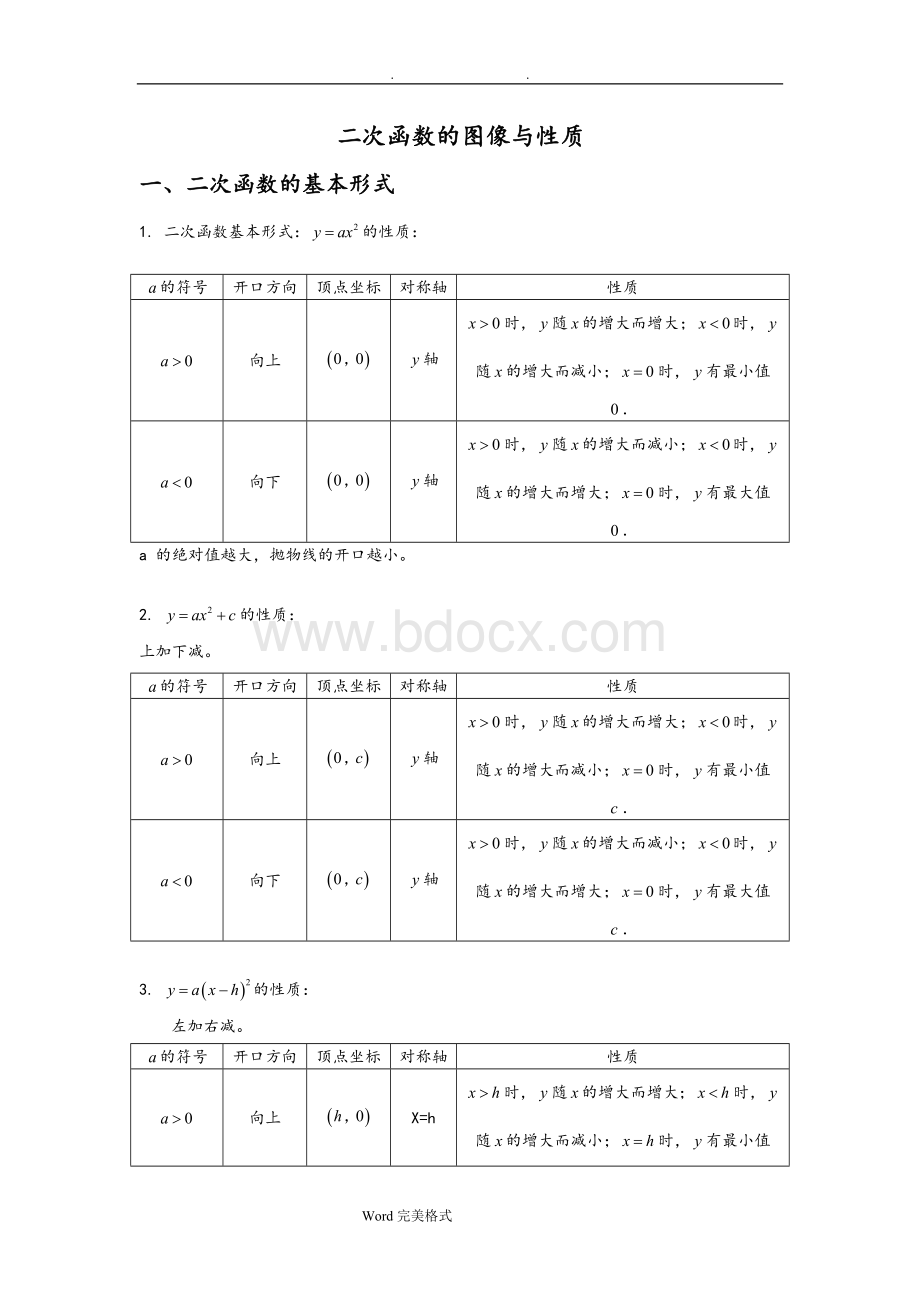
3.的性质：

左加右减。

X=h

4.的性质：

二、二次函数图象的平移

1.平移步骤：

方法一：

⑴将抛物线解析式转化成顶点式，确定其顶点坐标；

⑵保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：

2.平移规律

在原有函数的基础上“值正右移，负左移；

值正上移，负下移”．

概括成八个字“左加右减，上加下减”．

方法二：

⑴沿轴平移:

向上（下）平移个单位，变成

（或）

⑵沿轴平移：

向左（右）平移个单位，变成（或）

三、二次函数与的比较

从解析式上看，与是两种不同的表达形式，后者通过配方可以得到前者，即，其中．

四、二次函数图象的画法

五点绘图法：

利用配方法将二次函数化为顶点式，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：

顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点，（若与轴没有交点，则取两组关于对称轴对称的点）.

画草图时应抓住以下几点：

开口方向，对称轴，顶点，与轴的交点，与轴的交点.

五、二次函数的性质

1.当时，抛物线开口向上，对称轴为，顶点坐标为．

当时，随的增大而减小；

当时，随的增大而增大；

当时，有最小值．

2.当时，抛物线开口向下，对称轴为，顶点坐标为．当时，随的增大而增大；

当时，有最大值．

六、二次函数解析式的表示方法

1.一般式：

（，，为常数，）；

2.顶点式：

3.两根式：

（，，是抛物线与轴两交点的横坐标）.

注意：

任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与轴有交点，即时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.

七、二次函数的图象与各项系数之间的关系

1.二次项系数

二次函数中，作为二次项系数，显然．

⑴当时，抛物线开口向上，的值越大，开口越小，反之的值越小，开口越大；

⑵当时，抛物线开口向下，的值越小，开口越小，反之的值越大，开口越大．

总结起来，决定了抛物线开口的大小和方向，的正负决定开口方向，的大小决定开口的大小．

2.一次项系数

在二次项系数确定的前提下，决定了抛物线的对称轴．

⑴在的前提下，

当时，，即抛物线的对称轴在轴左侧；

当时，，即抛物线的对称轴就是轴；

当时，，即抛物线对称轴在轴的右侧．

⑵在的前提下，结论刚好与上述相反，即

当时，，即抛物线的对称轴在轴右侧；

当时，，即抛物线对称轴在轴的左侧．

总结起来，在确定的前提下，决定了抛物线对称轴的位置．

的符号的判定：

对称轴在轴左边则，在轴的右侧则，概括的说就是“左同右异”

总结：

3.常数项

⑴当时，抛物线与轴的交点在轴上方，即抛物线与轴交点的纵坐标为正；

⑵当时，抛物线与轴的交点为坐标原点，即抛物线与轴交点的纵坐标为；

⑶当时，抛物线与轴的交点在轴下方，即抛物线与轴交点的纵坐标为负．

总结起来，决定了抛物线与轴交点的位置．

总之，只要都确定，那么这条抛物线就是唯一确定的．

二次函数解析式的确定：

根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：

1.已知抛物线上三点的坐标，一般选用一般式；

2.已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；

3.已知抛物线与轴的两个交点的横坐标，一般选用两根式；

4.已知抛物线上纵坐标相同的两点，常选用顶点式．

八、二次函数图象的对称

二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达

1.关于轴对称

关于轴对称后，得到的解析式是；

关于轴对称后，得到的解析式是；

2.关于轴对称

3.关于原点对称

关于原点对称后，得到的解析式是；

4.关于顶点对称（即：

抛物线绕顶点旋转180°

）

关于顶点对称后，得到的解析式是；

关于顶点对称后，得到的解析式是．

5.关于点对称

关于点对称后，得到的解析式是

根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．

二次函数图像参考：

十一、

【例题精讲】

一、一元二次函数的图象的画法

【例1】求作函数的图象

【例2】求作函数的图像。

分析：

画二次函数图象步骤：

（1）配方；

（2）列表；

（3）描点成图；

也可利用图象的对称性，先画出函数的左（右）边部分图象，再利用对称性描出右（左）部分就可。

二、一元二次函数性质

【例3】求函数的最小值及图象的对称轴和顶点坐标，并求它的单调区间。

【例4】求函数图象的顶点坐标、对称轴、最值。

【点评】要研究二次函数顶点、对称轴、最值、单调区间等性质时，方法有两个：

（1）配方法；

如例3

（2）公式法：

适用于不容易配方题目（二次项系数为负数或分数）如例4，可避免出错。

任何一个函数都可配方成如下形式：

【二次函数题型总结】

1.关于二次函数的概念

例1如果函数是二次函数，那么m的值为。

例2抛物线的开口方向是；

对称轴是；

顶点为。

-1

O

X=1

Y

X

2.关于二次函数的性质及图象

例3函数的图象如图所示，

则a、b、c，，，的符号

为，

例4已知a－b＋c=09a＋3b＋c=0,则二次函数y=ax2＋bx＋c的图像的顶点可能在（）

（A）第一或第二象限（B）第三或第四象限

（B）（C）第一或第四象限（D）第二或第三象限

3.确定二次函数的解析式

3

o

y

x

例5已知：

函数的图象如图：

那么函数解析式为（）

（A）（B）

（C）（D）

4.一次函数图像与二次函数图像综合考查

例6已知一次函数y=ax+c二次函数y=ax2+bx+c（a≠0）,它们在同一坐标系中的大致图象是（）.

例7如图：

△ABC是边长为4的等边三角形，AB在X轴上，点C在第一象限，AC与Y轴交于点D，点A的坐标为（-1，0）

（1）求B、C、D三点的坐标；

（2）抛物线经过B、C、D三点，求它的解析式；

【练习题】

一、选择题

1.二次函数的顶点坐标是（）

A.（2,－11）B.（－2，7）C.（2，11）D.（2，－3）

2.把抛物线向上平移1个单位，得到的抛物线是（）

A.B.C.D.

3.函数和在同一直角坐标系中图象可能是图中的（）

4.已知二次函数的图象如图所示,则下列结论:

①a,b同号;

②当和时,函数值相等;

③④当时,的值只能取0.其中正确的个数是（）

A.1个B.2个C.3个D.4个

5.已知二次函数的顶点坐标（-1，-3.2）及部分图象（如图）,由图象可知关于的一元二次方程的两个根分别是（　　　）

Ａ．－１.３B.-2.3C.-0.3D.-3.3　

6.已知二次函数的图象如图所示，则点在（　）

A．第一象限　　　B．第二象限

C．第三象限　　D．第四象限

7.方程的正根的个数为（）

A.0个B.1个C.2个.3个

8.已知抛物线过点A（2,0）,B（-1,0）,与轴交于点C,且OC=2.则这条抛物线的解析式为

A.B.

C.或D.或

二、填空题

9．二次函数的对称轴是，则_______。

10．已知抛物线y=-2（x+3）²

+5，如果y随x的增大而减小，那么x的取值范围是_______.

11．一个函数具有下列性质：

①图象过点（－1，2），②当＜0时，函数值随自变量的增大而增大；

满足上述两条性质的函数的解析式是（只写一个即可）。

12．抛物线的顶点为C，已知直线过点C，则这条直线与两坐标轴所围成的三角形面积为。

13.二次函数的图象是由的图象向左平移1个单位,再向下平移2个单位得到的,则b=,c=。

14．如图，一桥拱呈抛物线状，桥的最大高度是16米，跨度是40米，在线段AB上离中心M处5米的地方，桥的高度是　　（π取3.14）.　　　　

三、解答题：

15.已知二次函数图象的对称轴是,图象经过（1,-6）,且与轴的交点为（0,）.

（1）求这个二次函数的解析式;

（2）当x为何值时,这个函数的函数值为0?

（3）当x在什么范围内变化时,这个函数的函数值随x的增大而增大?

第15题图

16.某种爆竹点燃后，其上升高度h（米）和时间t（秒）符合关系式（0<

t≤2），其中重力加速度g以10米/秒2计算．这种爆竹点燃后以v0=20米/秒的初速度上升，

（1）这种爆竹在地面上点燃后，经过多少