三角函数的图像和性质知识点及例题讲解Word下载.doc

三角函数的图像和性质知识点及例题讲解Word下载.doc

《三角函数的图像和性质知识点及例题讲解Word下载.doc》由会员分享，可在线阅读，更多相关《三角函数的图像和性质知识点及例题讲解Word下载.doc（6页珍藏版）》请在冰豆网上搜索。

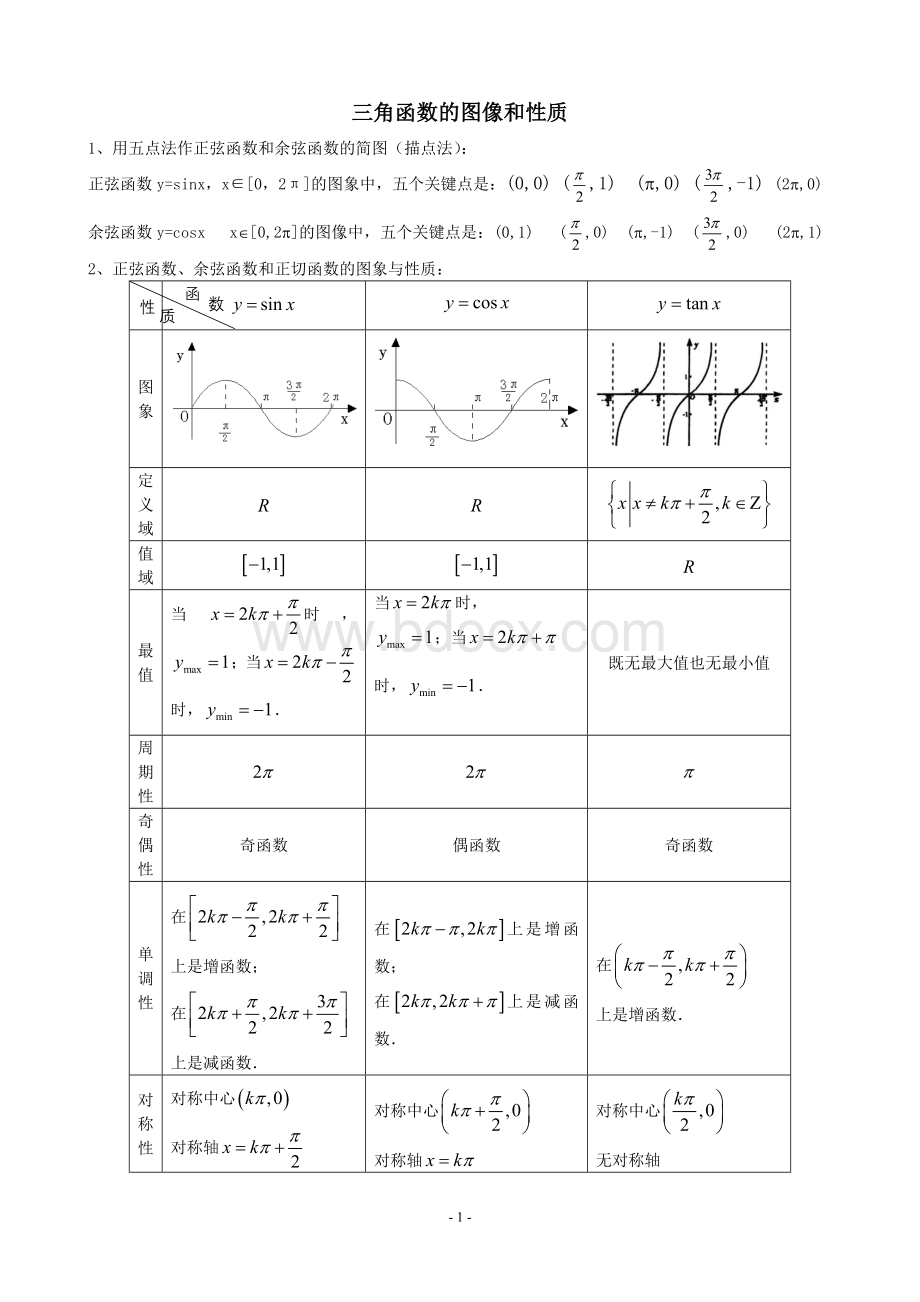
最值

当时，；

当

时，．

当时，

；

当

既无最大值也无最小值

周期性

奇偶性

奇函数

偶函数

单调性

在

上是增函数；

上是减函数．

在上是增函数；

在上是减函数．

上是增函数．

对称性

对称中心

对称轴

无对称轴

例作下列函数的简图

（1）y=|sinx|，x∈[0，2π]，

（2）y=-cosx，x∈[0，2π]

例利用正弦函数和余弦函数的图象，求满足下列条件的x的集合：

3、周期函数定义：

对于函数，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有：

，那么函数就叫做周期函数，非零常数T叫做这个函数的周期。

注意：

周期T往往是多值的（如2p,4p,…,-2p,-4p,…都是周期）周期T中最小的正数叫做的最小正周期（有些周期函数没有最小正周期）,的最小正周期为2p（一般称为周期）

正弦函数、余弦函数：

。

正切函数：

例求下列三角函数的周期：

1°

y=sin（x+）2°

y=cos2x3°

y=3sin（+）4°

y=tan3x

例求下列函数的定义域和值域：

（1）

（2）（3）

例5求函数的单调区间

例不求值，比较大小

（1）sin（－）、sin（－）；

（2）cos（－）、cos（－）．

解：

（1）∵－＜－＜－＜．

（2）cos（－）＝cos＝cos

且函数y＝sinx，x∈［－，］是增函数cos（－）＝cos＝cos

∴sin（－）＜sin（－）∵0＜＜＜π

即sin（－）－sin（－）＞0且函数y＝cosx，x∈［0，π］是减函数

∴cos＜cos

即cos－cos＜0

∴cos（－）－cos（－）＜0

4、函数的图像：

（1）函数的有关概念：

①振幅：

②周期：

③频率：

④相位：

⑤初相：

．

（2）振幅变换

①y=Asinx，xÎ

R（A>

0且A¹

1）的图象可以看作把正数曲线上的所有点的纵坐标伸长（A>

1）或缩短（0<

A<

1）到原来的A倍得到的

②它的值域[-A,A]最大值是A,最小值是-A

③若A<

0可先作y=-Asinx的图象，再以x轴为对称轴翻折

A称为振幅，这一变换称为振幅变换

（3）周期变换

①函数y=sinωx,xÎ

R（ω>

0且ω¹

1）的图象，可看作把正弦曲线上所有点的横坐标缩短（ω>

1）或伸长（0<

ω<

1）到原来的倍（纵坐标不变）

②若ω<

0则可用诱导公式将符号“提出”再作图

ω决定了函数的周期，这一变换称为周期变换

（4）相位变换

一般地，函数y＝sin（x＋），x∈R（其中≠0）的图象，可以看作把正弦曲线上所有点向左（当＞0时）或向右（当＜0时＝平行移动｜｜个单位长度而得到（用平移法注意讲清方向：

“加左”“减右”）

y＝sin（x＋）与y＝sinx的图象只是在平面直角坐标系中的相对位置不一样，这一变换称为相位变换

5、小结平移法过程（步骤）

作y=sinx（长度为2p的某闭区间）

得y=sin（x+φ）

得y=sinωx

得y=sin（ωx+φ）

得y=Asin（ωx+φ）的图象，先在一个周期闭区间上再扩充到R上。

沿x轴平移|φ|个单位

横坐标伸长或缩短

横坐标伸长或缩短

沿x轴平移||个单位

纵坐标伸长或缩短

图e

6、函数，当时，取得最小值为；

当时，取得最大值为，则，，．

例如图e，是f（x）＝Asin（ωx＋φ），A＞0，｜φ｜＜的一段图象，则f（x）的表达式为

例如图b是函数y＝Asin（ωx＋φ）＋2的图象的一部分，它的振幅、周期、初相各是（）

AA＝3，Ｔ＝，φ＝－

BA＝1，Ｔ＝，φ＝－

CA＝1，Ｔ＝，φ＝－

DA＝1，Ｔ＝，φ＝－

例画出函数y＝3sin（2x＋），x∈R的简图

（五点法）由T＝，得T＝π列表：

x

–

2x+

π

2π

3sin（2x+）

3

–3

例求函数的定义域、值域，并指出它的周期性、奇偶性、单调性

由得，

所求定义域为

值域为R，周期，是非奇非偶函数

在区间上是增函数

例已知函数y=sin2x+cos2x-2

（1）用“五点法”作出函数在一个周期内的图象

（2）求这个函数的周期和单调区间

（3）求函数图象的对称轴方程

（4）说明图象是由y=sinx的图象经过怎样的变换得到的

y=sin2x+cos2x-2=2sin（2x+）-2

（1）列表

2

-2

-4

其图象如图示

（2）=π

由-+2kπ≤2x+≤+2kπ，知函数的单调增区间为

［-π+kπ,+kπ］,k∈Z

由+2kπ≤2x+≤π+2kπ，知函数的单调减区间为

［+kπ,π+kπ］,k∈Z

（3）由2x+=+kπ得x=+π

∴函数图象的对称轴方程为x=+π,（k∈Z）

（4）把函数y1=sinx的图象上所有点向左平移个单位，得到函数y2=sin（x+）的图象；

再把y2图象上各点的横坐标缩短到原来的倍（纵坐标不变），得到y3=sin（2x+）的图象；

再把y3图象上各点的纵坐标伸长到原来的2倍（横坐标不变），得到y4=2sin（2x+）的图象；

最后把y4图象上所有点向下平移2个单位，得到函数y=2sin（2x+）-2的图象

-6-