函数的极值教案Word文档下载推荐.doc

函数的极值教案Word文档下载推荐.doc

《函数的极值教案Word文档下载推荐.doc》由会员分享，可在线阅读，更多相关《函数的极值教案Word文档下载推荐.doc（8页珍藏版）》请在冰豆网上搜索。

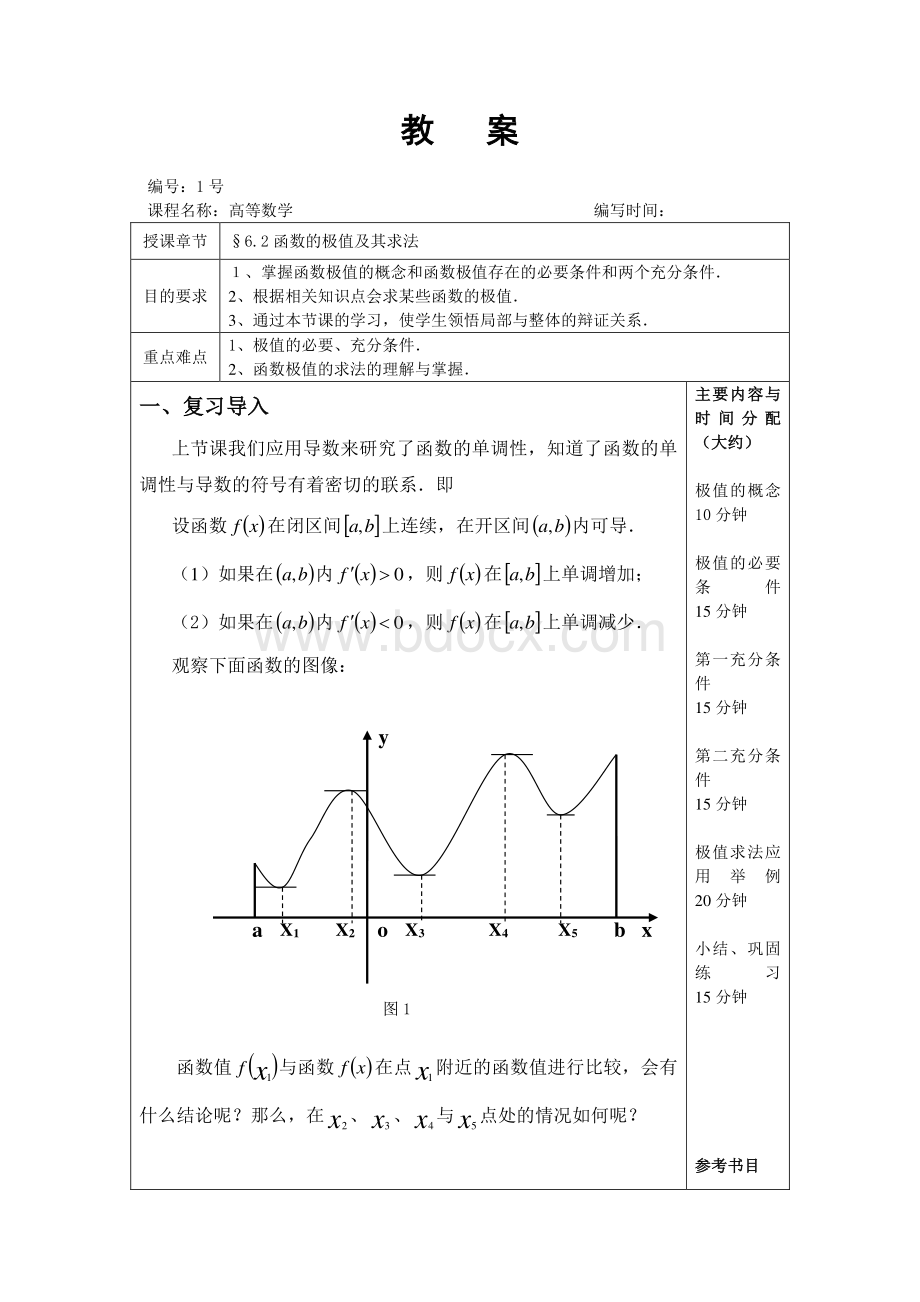
图1函数值（）xf1与函数（）xf在点x1附近的函数值进行比较，会有什么结论呢？

那么，在x2、x3、x4与x5点处的情况如何呢？

主要内容与主要内容与时间分配时间分配（大约）（大约）极值的概念10分钟极值的必要条件15分钟第一充分条件15分钟第二充分条件15分钟极值求法应用举例20分钟小结、巩固练习15分钟参考书目参考书目xboaX1X2X3X4X5y二、探究新课二、探究新课

（一）、

（一）、函数极值的定义函数极值的定义定义定义11设函数（）xf在点x0的某一邻域（）xU0内有定义，如果对于去心邻域0U（）x0内的任一x，都有（）（）xfxf0（或（）（）xfxf0）则称函数值（）xf0是函数（）xf的一个极大值（或极小值）函数的极大值与极小值统称为函数的极值，使函数取得极值的点称为极值点对极值定义的理解对极值定义的理解：

1、函数的极大值、极小值概念是局部性的概念2、函数的极大值不一定比极小值大3、函数的极值点一定出现在区间内部（二二）、函数）、函数存在存在极值的极值的必要条件必要条件观察图1，极值点处的切线有什么特点？

结合导数的几何意义，我们能否得到什么样的结论？

定理定理1极值的必要条件设函数（）xf在x0处可导，且在x0处取得极值，则一定有（）00=xf分析：

分析：

我们知道函数的极值就是局部的最值，而证明极值点处的导数为零只要在极值点的某一邻域内考虑即可，那么就是证明这一邻域内的最值处导数为零，而这实际上就是费马（Fermat）引理的内容证明：

证明：

设（）xf0为极大值（（）xf0为极小值时可类似证明）根据极值的定义，对于0Ux（）x0，恒有（）（）xfxf0，于是当xx0，（）（）000xxxfxf，故（）（）（）00lim000=xxxxfxfxfx当xx0，（）（）000xxxfxf，故（）（）（）00lim000=+xxxxfxfxfx1、高等数学辽宁省师范院校初等教育专业教材2、高等数学同济大学第五版从而，（）00=xf（三）、函数存在极（三）、函数存在极值的充分条件值的充分条件定义定义22使导数（）0=xf的点称为函数的驻点（稳定点）定理1表明：

可导函数的极值点必定是驻点。

讨论讨论：

1、函数的驻点一定是极值点吗？

2、函数的导数不存在的点可能是极值点吗？

3、观察图1，极大值点与极小值点左右两侧的函数的导数符号如何变化？

注意注意：

驻点不一定是极值点，例如函数（）xxf3=的驻点0=x就不是极值点定理1表明，对可导函数而言求极值点应先找出驻点，然后对驻点进行判断，哪些是极值点哪些不是极值点根据极值的定义及函数单调性的判定法不难知道：

如果在驻点两侧函数导数的符号相反，则驻点必然是使函数单调性改变的点，从而一定是函数的极值点由此我们得到下面的定理定理定理2（极值的第一充分条件）设函数（）xf在点x0处连续，且在点x0的某一邻域（）xU0（点x0可除外）内具有导数，对于0Ux（）x0，

（1）若当xx0时，（）0xf，当xx0，（）0xf，则（）xf0是函数（）xf的极大值；

（2）若当xx0时，（）0xf，当xx0，（）0xf，则（）xf0是函数（）xf的极小值；

（3）若在x0两侧，（）xf的符号相同，则（）xf0不是（）xf的极值分析：

显然

（1）与

（2）的证明是类似的由于证明极值是比较x0处的函数值与其邻域内的其它点处的函数值，而拉格朗日（Lagrange）中值定理就是讨论函数值之差与自变量之差之间的关系的，因此应用拉格朗日（Lagrange）中值定理可证明证证明：

明：

仅证，设x为0U（）x0内任意一点，根据拉格朗日（Lagrange）中值定理得（）（）（）（）（）之间与在xxxxxffxf000=由

（1）的条件可知：

当xx0时，（）0xf，所以（）（）00xxf，所以（）（）xfxf0；

当xx0，（）0xf，所以（）（）00xxf，所以（）（）xfxf0对于0U（）x0内任意一点x，都有（）（）xfxf0根据极值的定义知（）xf0是函数（）xf的极大值

（2）、（3）的证明是类似的，建议学生给出定理2表明：

如果在点x0两侧的导数符号相反，x0就一定是极值点，如果在点x0两侧的导数符号相同，则x0就一定不是极值点问题：

问题：

根据定理2能否寻求到求函数极值的方法？

求极值的步骤：

（1）求出导数（）xf；

（2）求出（）xf的全部驻点和不可导点；

（3）根据定理2确定这些点是不是极值点，如果是极值点，进一步确定是极大值点还是极小值点；

（4）求出各极值点处的函数值,就得到函数（）xf的全部极值应用举例：

应用举例：

例1求函数（）59323+=xxfxx的极值解该函数的定义域为（）+,（）（）（）3139632+=xxxxfx令（）0=xf，得驻点11=x，32=x驻点将定义域分成三部分，现列表讨论如下：

x（）1,-1（）3,13（）+,3（）xf+0-0+（）xf极大值极小值由表可知，函数（）xf在1=x处取得极大值，极大值为（）101=f；

在3=x处取得极小值，极小值为（）223=f上述有关极值的充分条件和必要条件都是对可导函数而言的，在此条件下，极值点一定是驻点，因此只要求出函数的驻点，再由定理2考察各个驻点是否为极值点就行了但是如果函数有不可导点，就不能肯定极值点一定是驻点了，因为在导数不存在的点处，函数也可能取得极值。

请看下例：

例例2求函数（）（）2321=xxf的极值解该函数的定义域为（）+,当2x时，（）32132=xxf；

当2=x时，（）xf不存在当2x时，（）0xf；

当2x时，（）0xf，又（）xf在2=x处连续，所以2=x是函数（）xf的极大值点，极大值为（）12=f注意：

注意：

以上是利用函数的一阶导数来讨论函数的极值，当函数在驻点处的二阶导数存在且不为零时，也可以利用下面的定理用二阶导数来判断函数在驻点处是取得极大值还是极小值定理定理3极值的第二充分条件设函数（）xf在点x0处具有二阶导数，且（）00=xf，（）00xf，则

（1）当（）00xf时，函数（）xf在点x0处取得极大值；

（2）当（）00xf时，函数（）xf在点x0处取得极小值证明只证情形，情形的证明是类似的由导数的定义及（）00=xf和（）00xf，得（）（）（）（）0limlim000000=xxxxxxfxxfxfxfxx根据函数极限的局部保号性定理，对于0Ux（）x0，有（）00xxxf因此，当xx0时，（）0xf；

当xx0，（）0xf根据定理2，函数（）xf在点x0处取得极大值定理3表明，如果函数（）xf在其驻点x0处的二阶导数（）00xf，则驻点x0一定是函数（）xf的极值点注意注意：

如果（）00=xf，就不能用定理3来判断x0是否为极值点事实上，当（）00=xf，（）00=xf，（）xf在x0处可能有极大值，也可能有极小值，也可能没有极值例如（）xxf4=，（）xxg4=，（）xxh3=，这三个函数就分别属于这三种情况。

所以，当函数在驻点处的二阶导数为零时，只能用定理2来判断，即：

由驻点左右两侧一阶导数的符号来判断应用举例：

例例3求函数（）（）1213+=xxf的极值解：

（）（）1622=xxxf令（）0=xf，得11=x，02=x，13=x（）（）（）151622=xxxf因（）060=f，所以（）xf在0=x处取得极小值，极小值为（）00=f又（）（）011=ff，此时定理3失效，仍用定理2来判断当1x时，（）0xf；

当01x时，（）0xf，所以（）xf在1=x处没有极值同理，（）xf在1=x处没有极值三、巩固练习三、巩固练习P167习题621、求下列函数的极值

（1）xxy2332=

（2）xxy+=12、a为何值时，函数（）xxaxf3sin31sin+=在3=x取得极值，它是极大值还是极小值，求此极值四、课堂小结四、课堂小结1、函数极值的概念2、函数存在极值的必要条件3、函数存在极值的充分条件4、求函数极值的方法五、思考题五、思考题1、证明：

定理2（第一充分条件）的

（2）、（3）结论2、求函数exxy=的极值3、试证明：

如果函数dcxbayxx+=23满足条件032acb，那么函数没有极值