高考数学多面体内切球棱柱棱锥内切球方法总结题型专练Word文档格式.docx
《高考数学多面体内切球棱柱棱锥内切球方法总结题型专练Word文档格式.docx》由会员分享,可在线阅读,更多相关《高考数学多面体内切球棱柱棱锥内切球方法总结题型专练Word文档格式.docx(4页珍藏版)》请在冰豆网上搜索。
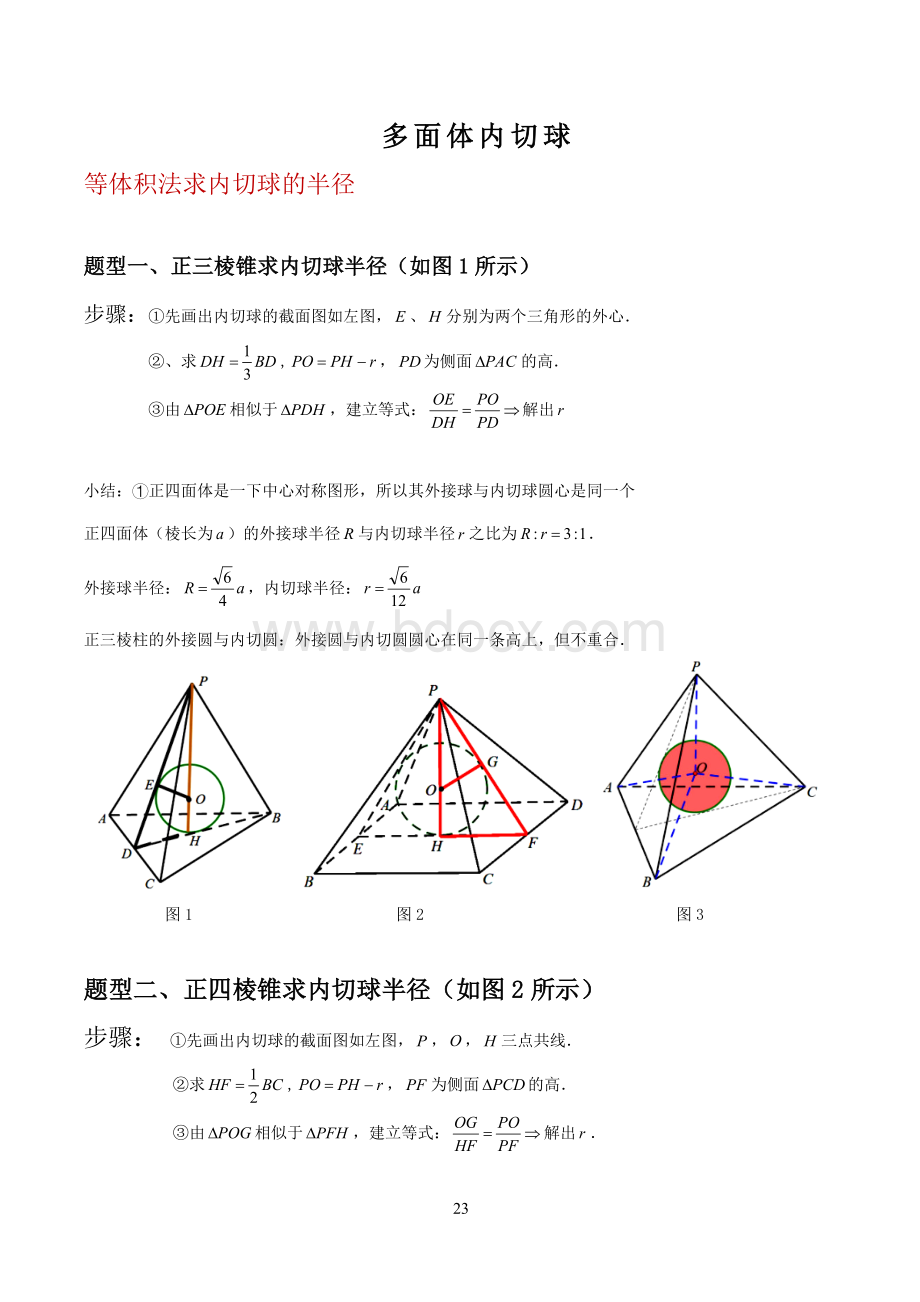
①先画出内切球的截面图如左图,、分别为两个三角形的外心.
②、求,,为侧面的高.
③由相似于,建立等式:
解出
小结:
①正四面体是一下中心对称图形,所以其外接球与内切球圆心是同一个
正四面体(棱长为)的外接球半径与内切球半径之比为.
外接球半径:
,内切球半径:
正三棱柱的外接圆与内切圆:
外接圆与内切圆圆心在同一条高上,但不重合.
图1图2图3
题型二、正四棱锥求内切球半径(如图2所示)
①先画出内切球的截面图如左图,,,三点共线.
②求,,为侧面的高.
解出.
题型三、求任意三棱锥的内切球半径:
等体积法(如图3所示)
①先求出四个表面的面积和整个锥体的体积.
②设内切球半径为,建立等式:
.
③解出.
例1已知正四面体,为底面的中心,为外接球的球心,设棱长为,外接球半径为,内切球半径为,求.
例2.已知三棱锥中,底面,,,,,则该三棱锥的内切球的体积为 .
例3一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为()
例4正三棱锥,底面边长为,侧棱长为,则其外接球和内切球的半径是多少?
例5.一个几何体的三视图如图所示,三视图都为腰长为2的等腰直角三角形,则该几何体的外接球半径与内切球半径之比为
A. B. C. D.
课后练习
1.如图是棱长为2的正八面体(八个面都是全等的等边三角形),球是该正八面体的内切球,则球的表面积为()
A. B. C. D.
2.若某正四面体内切球的体积为,则正四面体外接球的表面积为()
A. B. C. D.
3.底面边长为的正三棱锥的内切球半径为,则其外接球的表面积为()
4.如图,正方形的边长为,点,分别在边,上,且.将此正方形沿,,切割得到四个三角形,现用这四个三角形作为一个三棱锥的四个面,则该三棱锥的内切球的体积为 .
第1题图第4题图第8题图
5.若三棱锥中,,其余各棱长均为5,则三棱锥内切球的表面积为 .
6.在边长为2的菱形中,,将菱形沿对角线对折,使,则所得三棱锥的内切球的半径为 .
7.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(biēnà
o).已知在鳖臑中,平面,,则该鳖臑的外接球与内切球的表面积之和为 .
8.如图,已知正四面体的高为,则它的内切球的体积为 .
9.已知三棱锥的底面是等腰三角形,,底面,,则这个三棱锥内切球的半径为 .
10.在边长为的菱形中,,将菱形沿对角线对折,使二面角的余弦值为,则所得三棱锥的内切球的表面积为 .
26