一元二次方程知识点总结及典型习题.doc

一元二次方程知识点总结及典型习题.doc

《一元二次方程知识点总结及典型习题.doc》由会员分享，可在线阅读，更多相关《一元二次方程知识点总结及典型习题.doc（13页珍藏版）》请在冰豆网上搜索。

一元二次方程

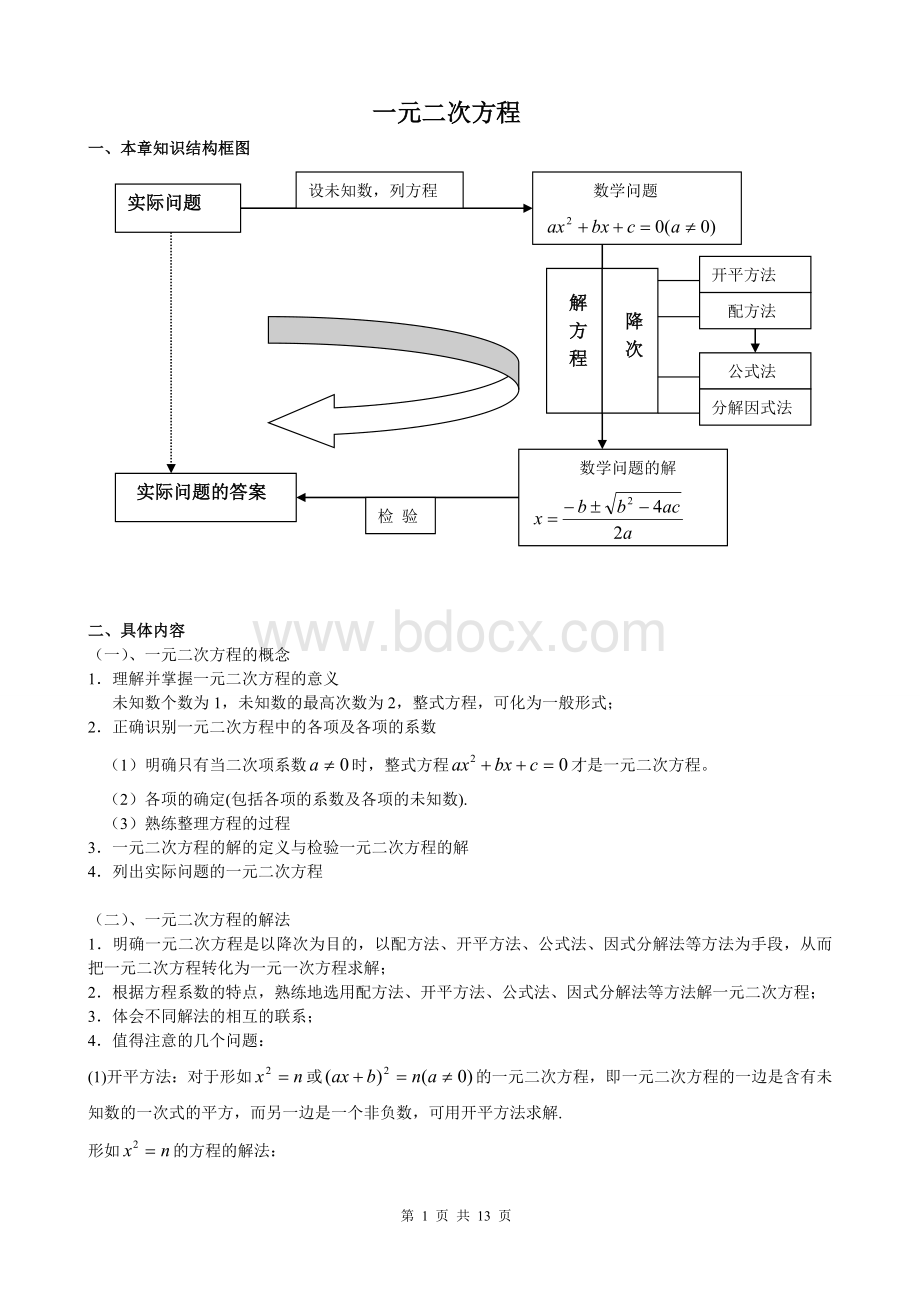
一、本章知识结构框图

实际问题

数学问题

设未知数，列方程

实际问题的答案

数学问题的解

解方程

降次

开平方法

配方法

公式法

分解因式法

检验

二、具体内容

（一）、一元二次方程的概念

1．理解并掌握一元二次方程的意义

未知数个数为1，未知数的最高次数为2，整式方程，可化为一般形式；

2．正确识别一元二次方程中的各项及各项的系数

（1）明确只有当二次项系数时，整式方程才是一元二次方程。

（2）各项的确定（包括各项的系数及各项的未知数）.

（3）熟练整理方程的过程

3．一元二次方程的解的定义与检验一元二次方程的解

4．列出实际问题的一元二次方程

（二）、一元二次方程的解法

1．明确一元二次方程是以降次为目的，以配方法、开平方法、公式法、因式分解法等方法为手段，从而把一元二次方程转化为一元一次方程求解；

2．根据方程系数的特点，熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程；

3．体会不同解法的相互的联系；

4．值得注意的几个问题：

（1）开平方法：

对于形如或的一元二次方程，即一元二次方程的一边是含有未知数的一次式的平方，而另一边是一个非负数，可用开平方法求解.

形如的方程的解法：

当时，;

当时，;

当时，方程无实数根。

（2）配方法：

通过配方的方法把一元二次方程转化为的方程，再运用开平方法求解。

配方法的一般步骤：

①移项：

把一元二次方程中含有未知数的项移到方程的左边，常数项移到方程的右边；

②“系数化1”：

根据等式的性质把二次项的系数化为1；

③配方：

将方程两边分别加上一次项系数一半的平方，把方程变形为的形式；

④求解：

若时，方程的解为，若时，方程无实数解。

（3）公式法：

一元二次方程的根

当时，方程有两个实数根,且这两个实数根不相等；

当时，方程有两个实数根,且这两个实数根相等，写为；

当时，方程无实数根.

公式法的一般步骤：

①把一元二次方程化为一般式；②确定的值；③代入中计算其值，判断方程是否有实数根；④若代入求根公式求值，否则，原方程无实数根。

（因为这样可以减少计算量。

另外，求根公式对于任何一个一元二次方程都适用，其中也包括不完全的一元二次方程。

）

（4）因式分解法：

①因式分解法解一元二次方程的依据：

如果两个因式的积等于0，那么这两个因式至少有一个为0，即：

若，则；

②因式分解法的一般步骤：

若方程的右边不是零，则先移项，使方程的右边为零；把方程的左边分解因式；令每一个因式都为零，得到两个一元一次方程；解出这两个一元一次方程的解可得到原方程的两个解。

（5）选用适当方法解一元二次方程

①对于无理系数的一元二次方程，可选用因式分解法，较之别的方法可能要简便的多，只不过应注意二次根式的化简问题。

②方程若含有未知数的因式，选用因式分解较简便，若整理为一般式再解就较为麻烦。

（6）解含有字母系数的方程

（1）含有字母系数的方程，注意讨论含未知数最高项系数，以确定方程的类型；

（2）对于字母系数的一元二次方程一般用因式分解法解，不能用因式分解的可选用别的方法，此时一定不要忘记对字母的取值进行讨论。

（三）、根的判别式

1．了解一元二次方程根的判别式概念，能用判别式判定根的情况，并会用判别式求一元二次方程中符合题意的参数取值范围。

（1）=

（2）根的判别式定理及其逆定理：

对于一元二次方程（）

①当方程有实数根；

（当方程有两个不相等的实数根；当方程有两个相等的实数根；）

②当方程无实数根；

从左到右为根的判别式定理；从右到左为根的判别式逆定理。

2．常见的问题类型

（1）利用根的判别式定理，不解方程，判别一元二次方程根的情况

（2）已知方程中根的情况，如何由根的判别式的逆定理确定参数的取值范围

（3）应用判别式，证明一元二次方程根的情况

①先计算出判别式（关键步骤）；

②用配方法将判别式恒等变形；

③判断判别式的符号；

④总结出结论.

例：

求证：

方程无实数根。

（4）分类讨论思想的应用：

如果方程给出的时未指明是二次方程，后面也未指明两个根，那一定要对方程进行分类讨论，如果二次系数为0，方程有可能是一元一次方程；如果二次项系数不为0，一元二次方程可能会有两个实数根或无实数根。

（5）一元二次方程根的判别式常结合三角形、四边形、不等式（组）等知识综合命题，解答时要在全面分析的前提下，注意合理运用代数式的变形技巧

（6）一元二次方程根的判别式与整数解的综合

（7）判别一次函数与反比例函数图象的交点问题

（四）、一元二次方程的应用

1.数字问题：

解答这类问题要能正确地用代数式表示出多位数，奇偶数，连续整数等形式。

2.几何问题：

这类问题要结合几何图形的性质、特征、定理或法则来寻找等量关系，构建方程，对结果要结合几何知识检验。

3.增长率问题（下降率）：

在此类问题中，一般有变化前的基数（），增长率（），变化的次数（），变化后的基数（）,这四者之间的关系可以用公式表示。

4.其它实际问题（都要注意检验解的实际意义，若不符合实际意义，则舍去）。

（五）新题型与代几综合题

（1）有100米长的篱笆材料，想围成一矩形仓库，要求面积不小于600平方米，在场地的北面有一堵50米的旧墙，有人用这个篱笆围成一个长40米、宽10米的仓库，但面积只有400平方米，不合要求，问应如何设计矩形的长与宽才能符合要求呢？

（2）读诗词解题（列出方程，并估算出周瑜去世时的年龄）：

大江东去浪淘尽，千古风流数人物，而立之年督东吴，英年早逝两位数，十位恰小个位三，个位平方与寿符，哪位学子算得准，多少年华属周瑜？

（36岁）

（3）已知：

分别是的三边长，当时，关于的一元二次方程有两个相等的实数根，求证：

是直角三角形。

（4）已知：

分别是的三边长，求证：

方程没有实数根。

（5）当是什么整数时，关于的一元二次方程与的根都是整数？

（）

（6）已知关于的方程，其中为实数，

（1）当为何值时，方程没有实数根？

（2）当为何值时，方程恰有三个互不相等的实数根？

求出这三个实数根。

答案：

（1）

（2）.

（六）相关练习

（一）一元二次方程的概念

1．一元二次方程的项与各项系数

把下列方程化为一元二次方程的一般形式，再写出二次项，一次项，常数项：

（1）

（2）

（3）

（4）

（5）

2．应用一元二次方程的定义求待定系数或其它字母的值

（1）为何值时，关于的方程是一元二次方程。

（）

（2）若分式，则（）

3．由方程的根的定义求字母或代数式值

（1）关于的一元二次方程有一个根为0，则（）

（2）已知关于的一元二次方程有一个根为1，一个根为，则，（0，0）

（3）已知c为实数，并且关于的一元二次方程的一个根的相反数是方程的一个根，求方程的根及c的值。

（0，-3，c=0）

（二）一元二次方程的解法

1．开平方法解下列方程：

（1）（）

（2）（）

（3）（原方程无实根）（4）（）

（5）（）

2．配方法解方程：

（1）（）

（2）（）

（3）（）

3．公式法解下列方程：

（1）（）

（2）（）

（3）（）（4）（原方程无实数根）

（5）（）

4．因式分解法解下列方程：

（1）（）

（2）（）

（3）（）（4）（）

（5）（）（6）（）

（7）（）

5．解法的灵活运用（用适当方法解下列方程）：

（1）（）

（2）（）

（3）（）

（4）（）

（5）（）

6．解含有字母系数的方程（解关于x的方程）：

（1）（）

（2）（）

（3）（）（）

（4）（讨论a）

（三）一元二次方程的根的判别式

1．不解方程判别方程根的情况：

（1）4（有两个不等的实数根）

（2）（无实数根）

（3）（有两个相等的实数根）

2．为何值时，关于x的二次方程

（1）有两个不等的实数根（）

（2）有两个相等的实数根（）

（3）无实数根（）

3．已知关于ｘ的方程有两个相等的实数根．求ｍ的值和这个方程的根．

（或）

4．若方程有实数根，求：

正整数a.（）

5．对任意实数m，求证：

关于x的方程无实数根.

6．为何值时，方程有实数根.

（当时，原方程有一个实数根，；

当时，解得，所以当且时方程有两个实数根。

综上所述，当时，方程有实数根.）

7．设为整数，且时，方程有两个相异整数根，求的值及方程的根。

（当=12时，方程的根为；当=24时，方程的根为）

（四）一元二次方程的应用

1．已知直角三角形三边长为三个连续整数，求它的三边长和面积.（3，4，5，面积为6）

2．一个两位数，个位上的数字比十位上的数字少4，且个位数字与十位数字的平方和比这个两位数小4，求这个两位数.（84）

3．某印刷厂在四年中共印刷1997万册书，已知第一年印刷了342万册，第二年印刷了500万册，如果以后两年的增长率相同，那么这两年各印刷了多少万册？

（550,605）

4．某人把5000元存入银行，定期一年到期后取出300元，将剩余部分（包括利息）继续存入银行，定期还是一年，且利率不变，到期如果全部取出，正好是275元，求存款的年利率？

（不计利息税）（10℅）

5．某商场销售一批名牌衬衫，平均每天可以售出20件，每件盈利40元，为了扩大销售增加盈利，尽快减少库存，商场决定采取适当降价措施，经调查发现，如果每件衬衫每降价1元，商场每天可多售出2件，若商场平均每天要盈利1200元，每件衬衫应降价多少元？