初中数学章节专项《相交线与平行线》教案.docx

初中数学章节专项《相交线与平行线》教案.docx

《初中数学章节专项《相交线与平行线》教案.docx》由会员分享，可在线阅读，更多相关《初中数学章节专项《相交线与平行线》教案.docx（18页珍藏版）》请在冰豆网上搜索。

初中数学章节专项《相交线与平行线》教案

相交线与平行线

一、本章学习目标

1、在具体情境中了解邻补角、对顶角的概念，知道对顶角相等。

了解垂线、垂线段等概念，知道过一点有且仅有一条直线垂直于已知直线。

会用三角尺或量角器过一点画一条直线的垂线。

了解垂线段最短的性质，体会点到直线距离的定义，并会度量点到直线的距离。

2、了解平行线的概念，知道平行公理及其推论，会用三角尺和直尺过直线外一点画这条直线的平行线。

能识别同位角、内错角、同旁内角。

掌握两直线平行的性质和判定方法。

3、理解图形平移后的对应点连线平行且相等的性质。

能够按照要求作出简单平面图形平移之后的图形。

能利用平移进行简单的图案设计，认识平移在现实生活中的应用

4、了解命题的概念，能初步区分命题的题设和结论。

了解命题真假及定理的含义。

理解本章学习的关于描述图形形状和位置关系的语句，会用这些语句描述简单的图形，会根据描述的语句画出图形。

能结合一些具体内容进行说理和简单推理，初步树立言之有据的意识

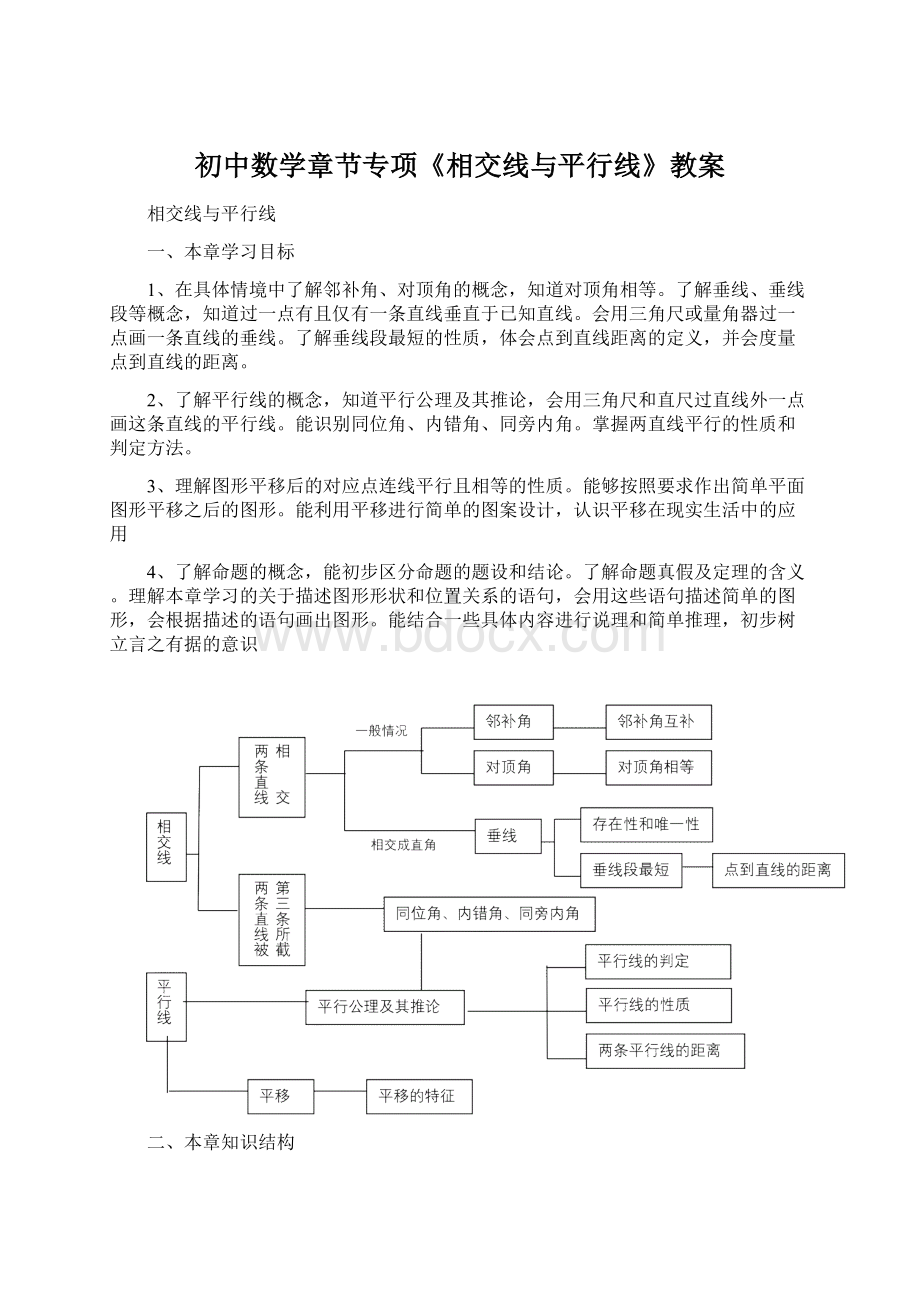
二、本章知识结构

基本知识

1.相交线：

两条不同的直线有一个公共点，称这两条直线相交，这个公共点称为交点。

2.对顶角：

两条直线相交，有一个公共点，没有公共边的两个角，称为对顶角。

3.对顶角的性质：

对顶角相等。

4.邻补角：

两条直线相交，有一条公共边，另一边互为反向延长线的两个角，称为邻补角。

5.邻补角的性质：

邻补角互补。

6.垂线：

当两条直线相交所成的四个角中，有一个角为直角，就说这两条直线垂直，其中一条直线叫另一条直线的垂线，它们的交点叫做垂足。

7.垂线的性质：

①在同一平面内，经过直线外或直线上一点，有且只有一条直线与已知直线垂直。

②连接直线外一点与直线上各点的所有线段中，垂线段最短，简述为垂线段最短。

8.点到直线的距离：

直线外一点到这条直线的垂线段的长度。

9.平行线：

在同一平面内，不相交的两条直线叫做平行线。

10.平行公理：

经过直线外一点有且只有一条直线与已知直线平行。

11.平行公理的推论：

如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

12.同位角：

两条直线被第三条直线所截，如果两个角分别在两条直线的相同一侧，并且在第三条直线的同旁，那么这两个角叫做同位角。

13.内错角：

两条直线被第三条直线所截，如果两个角在两条直线之间，并且分别在第三条直线的两侧，那么这两个角叫内错角。

14.同旁内角：

两条直线被第三条直线所截，如果两个在两条直线之间，并且分别在第三条直线的同旁，那么这两个角叫同旁内角

15.两条平行线间的距离：

同时垂直于两条平行线，并夹在这两条平行线间的线段长度。

16.平行线的判定：

①如果两条直线被第三条直线所截，同位角相等，两条直线平行。

②如果两条直线被第三条直线所截，内错角相等，两条直线平行。

③两条直线被第三条直线所截，同旁内角互补，两直线平行。

17.平行线的性质：

①两条直线平行，同位角相等。

②两条直线平行，内错角相等。

③两条直线平行，同旁内角互补。

18.平移：

某一基本的平面图形沿某一方向移动了一定的距离，这种图形的平行移动简称为平移。

19.平移的性质：

①把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同。

②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点，连接各组对应点的线段平行且相等。

20.平移的画法：

①首先要作出平移方向。

②确定平移距离。

③画出和已知图形相对应的对应点，顺次连接方式补充为完整的图形。

21.命题：

判断一件事情的语句

三、本章重点难点

1.重点是对顶角的概念与性质；垂线及垂线段的概念和性质；识别内错角、同位角、同旁内角；平行线的定义、平行公理，平行线的判定和性质；找出一个命题的题设和结论。

2.难点是应用对顶角性质进行有关的推理或计算；点到直线的距离的概念的认识；识别内错角、同位角、同旁内角；平行公理及推论的应用，利用判定公理，性质进行计算或证明和对推理的步骤的了解；找出一个命题的题设和结论。

四、本章中考内容及中考要求

了解对顶角，知道对顶角相等；了解垂线、垂线段等概念，了解垂线段最短的性质，理解点到直线的距离的意义；了解线段垂直平分线及其性质；知道过直线外一点有且仅有一条直线平行于已知直线；知道过一点有且仅有一条直线垂直于已知直线；理解两条平行之间距离的意义，会度量两条平行线之间的距离。

会用三角尺和直尺过已知直线外一点画这条直线的平行线；会三角尺或量角器过一点画一条直线的垂线；会运用线段垂直平分线的性质；掌握平行线的性质，会判断两条直线是否平行。

五、本章教学过程

（一）相交线

1、邻补角和对顶角

（1）邻补角的定义：

有一条公共边，另一边互为反向延长线，这种关系的两个角称为邻补角

（2）邻补角的性质：

邻补角互补

（3）对顶角：

两条直线相交，有一个公共点，没有公共边的两个角，称为对顶角

（4）对顶角的性质：

对顶角相等

例：

如图,直线a、b相交，∠1=40°,求∠2、∠3、∠4的度数。

解：

∵∠3=∠1（对顶角相等）

∠1=40°（已知）

∴∠3=40°（等量代换）

∴∠2=180°—∠1=140°（邻补角的定义）

∴∠4=∠2=140°（对顶角相等）

练习题一：

1、一个角的对顶角有个，邻补角最多有个，而补角则可以有个。

2、在下图中，∠1,∠2是对顶角的图形是（）

3、如图，直线AB交直线CD于O，OE是顶点为O的一条射线，图中的对顶角和邻补角各有（）组。

（A）1组，3组（B）2组，4组（C）2组，6组（D）3组，8组

4、如图，直线AB，CD相交于点O，且∠AOD+∠BOC=1000.则∠AOC是（）度

（A）1000

（B）900

（C）1500

（D）1300

5、如图，直线AB与直线CD相交于O，OE平分∠AOD，∠BOC=∠BOD—300，则∠COE的度数是（）

（A）1100

（B）142.50

（C）1500

（D）750

6、如图，已知三条直线两两相交，∠1=2∠3，∠2=85º，求∠4的度数。

7、如图，AB⊥CD于点O，EF经过点O，若∠1=25º，求∠2的度数。

8、如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2：

∠1=4：

1，求∠AOF的度数。

2、垂线

（1）垂线：

当两条直线相交所成的四个角中，有一个角为直角，就说这两条直线垂直，其中一条直线叫另一条直线的垂线，用符号“⊥”表示，如AB⊥CD读作“AB垂直于CD”，它们的交点叫做垂足。

（2）垂线的性质：

①在同一平面内，经过直线外或直线上一点，有且只有一条直线与已知直线垂直。

②连接直线外一点与直线上各点的所有线段中，垂线段最短，简述为垂线段最短。

（3）点到直线的距离：

直线外一点到这条直线的垂线段的长度。

垂线的画法：

①已知直线l，有多少条直线与已知直线l垂直？

——无数条

②过点A画直线BD的垂线

B·AD

A.

D图1B

在学生画出垂线的基础上，教师总结出用直角三角板画垂线的基本方法，强调用两条直角边“一贴”：

贴住已知直线，“一靠”：

靠住已知点再画线，并引导学生思考：

这样画出的为何是已知直线的垂线?

例1：

如图，直线AB、CD相交于点O，OE⊥AB，∠1=55°,求∠EOD的度数.

解:

∵AB⊥OE（已知）

∴∠EOB=90°（垂直的定义）

∵∠BOD=∠1=55°（对顶角相等）

∴∠EOD=∠EOB+∠BOD=90°+55°=145

例2：

如图,直线AB、CD相交于点O,OE⊥AB于O，OB平分∠DOF，∠DOE=50°,求∠AOC、∠EOF、∠COF的度数.

解：

∵AB⊥OE（已知）

∴∠EOB=90°（垂直的定义）

∵∠DOE=50°（已知）

∴∠DOB=40°（互余的定义）

∴∠AOC=∠DOB=40°（对顶角相等）

又∵OB平分∠DOF

∴∠BOF=∠DOB=40°（角平分线定义）

∴∠EOF=∠EOB+∠BOF=90°+40°=130°

∴∠COF=∠COD－∠DOF=180°－80°=100°（邻补角定义）

例3：

如图，∠ACB=90°，CD⊥AB能表示点到直线（或线段）距离的线段有（）

A、2条B、3条C、4条D、5条

练习题二：

1、在同一平面内，两条直线的位置关系只有两种_________

2、如图，若AB⊥CD，则∠ADC=____________

3、已知，在同一平面内，过点O作ON⊥AB，又过点O作OM⊥AB，所以OM与ON重合，其理由是（）

（A）过两点只有一条直线

（B）经过一点只有一条直线垂直于已知直线

（C）过一点只能作一条垂线

（D）垂线段最短

4、直线AB，CD相交于点O，OE⊥AB于O，且∠DOE=4∠COE，

则∠AOD的度数是（）

（A）1200（B）1500（C）980（D）1260

5、如图，AO⊥CO，BO⊥DO，若∠AOD=160º，求∠BOC的度数。

6、如图，∠ABD和∠CBD互为邻补角，∠CBD=

直角，BE平分∠ABD，BF⊥AC，求∠EBF的度数。

7、已知如图，O是直线CD上任意一点过点O引射线OA、OB、OE，使OE⊥OB，∠EOC与∠COA互为余角，∠EOC=53º，求∠BOD的度数。

8、如图，要从小河a引水到村庄A，请设计并作出一最佳路线，理由是：

__________

3、同位角、内错角、同旁内角

（1）同位角：

两条直线被第三条直线所截，如果两个角分别在两条直线的相同一侧，并且在第三条直线的同旁，那么这两个角叫做同位角。

（2）内错角：

两条直线被第三条直线所截，如果两个角在两条直线之间，并且分别在第三条直线的两侧，那么这两个角叫内错角。

（3）同旁内角：

两条直线被第三条直线所截，如果两个在两条直线之间，并且分别在第三条直线的同旁，那么这两个角叫同旁内角

例：

如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？

哪些是内错角？

哪些是同旁内角？

分析：

①CE是截线，由CE与其它线相交得到的角有哪几个？

②将这几个角抽出来，观察分析它们的位置关系

③再取其它的线为截线，再抽取与该截线相关的角来分析

解：

练习题三：

1、如图，∠ADE和∠CED是（）

A、同位角B、内错角C、同旁内角D、互为补角

2、如图，∠B与∠_____是直线______和直线_______被直线_________所截的同位角。

3、如图⑷，在∠1、∠2、∠3、∠4四个角中，

同位角有对，它们是，

内错角有对，它们是，

同旁内角有对，它们是；

4、图中，有几对同位角？

几对内错角？

几对同旁内角？

5、如图，∠1和∠2，∠3和∠4各是哪两条直线被哪一条直线所截形成的是什么角？

∠4与∠5呢？

∠2与∠6呢？

（二）平行线

1、平行线定义

（1）在同一平面内，不相交的两条直线叫做平行线。

用符号“∥”表示，如AB∥CD读作“AB平行于CD”

（2）平行公理：

经过直线外一点有且只有一条直线与已知直线平行。

（3）平行公理的推论：

如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

两条平行线的距离

　如图，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB与CD间的距离。

　注意：

直线AB∥CD，在直线AB上任取一点G，过点G作CD的垂线段GH，则垂线段GH的长度也就是直线AB与CD间的距离。

例：

判断下列说法是否正确

①直线AB与CD平行，记作AB∥CD

②线段a与直线AB垂直，记作a∥AB

③直线a与直线b互相垂直，记作a⊥b

④直线AB与直线CD互相垂直，记作AB⊥CD

答：

由定义知，①③④是正确的，而②是错误的

练习题四：

1、在同一平面内，两条直线的位置关系只有两种_________

2、若a⊥b，c⊥d则a与c的关系是（）

A、平行B、垂直C、相交D、以上都不对

3、公路两旁的两棵电线杆位置关系是__________________

4、下列说法正确的是（）

A、同一平面内不相交的两线段必平行

B、同一平面内不相交的两射线必平行

C、同一平面内不相交的一条线段与一条直线必平行

D、同一平面内不相交的两条直线必平行

5、已知直线l1和l2都经过点P，并且l1∥l3，l2∥l3，那么l1和l2必须重合，这是为什么？

2、平行线的判定

（1）如果两条直线被第三条直线所截，同位角相等，两条直线平行。

（2）如果两条直线被第三条直线所截，内错角相等，两条直线平行。

（3）两条直线被第三条直线所截，同旁内角互补，两直线平行。

例1：

看图填空，如图2—46

（1）因为∠1=∠E，（已知）

所以__________∥________（）

（2）因为∠2=∠D，（已知）

所以_________∥__________（）

（3）因为∠3=∠B（已知）

所以AB∥____________（）

例2：

如图，直线AB、CD被直线EF所截.量得∠1=60,∠2=120,就可以判定AB∥CD.它的根据是什么?

解法一：

∵∠1=60o　∠2=120o（已知）

∴∠1+∠2=180o

∵∠2=∠5

∴∠1+∠5=180o（等量代换）

∴AB∥CD（同旁内角互补、两直线平行）

解法二：

∵∠2=120o（已知）

∴∠3=60o（邻补角的定义）

∵∠1=60o（已知）

∴∠1=∠3（等量代换）

∴AB∥CD（同位角相等，两直线平行）

解法三：

∵∠2=120o（已知）

∴∠4=60o（邻补角的定义）

∵∠1=60o（已知）

∴∠1=∠4（等量代换）

∴AB∥CD（内错角相等，两直线平行）

练习题五：

1、如图AB∥CD∠1=∠2，∠3=∠4，试说明AD∥BE

解：

∵AB∥CD（已知）

∴∠4=∠_____（）

∵∠3=∠4（已知）

∴∠3=∠_____（）

∵∠1=∠2（已知）

∴∠1+∠CAF=∠2+∠CAF（）

即∠_____=∠_____（）

∴∠３＝∠_____

∴ＡＤ∥ＢＥ（）

2、如图，若已知∠D+

C=180°，可以判定直线和平行；若

1=

2，则可以判定直线和平行。

3、如图2—47已知：

∠1=40°，∠2=140°，说明：

AB∥CD

4、如图2—48ΔABC中，∠B=90°,D在AC边上，DF⊥BC于F，DE⊥AB于E，说明：

AB∥DF

5、如图，已知∠A+∠B=180º，∠A=∠C，可得到那些直线互相平行？

3、平行线的性质

（1）两条直线平行，同位角相等。

（2）两条直线平行，内错角相等。

（3）两条直线平行，同旁内角互补。

例1：

已知∠1＝∠B，求证：

∠2＝∠C

证明：

∵∠1＝∠B（已知）

　　　　　∴DE∥BC（同位角相等，两直线平行）

　　　　　∴∠2＝∠C（两直线平行，同位角相等）

例2：

用两块相同的三角板按如图所示的方式作平行线，

能解释其中道理的依据是。

答案：

内错角相等，两直线平行

例3：

已知：

如图，D、E、F分别是BC、CA、AB上的点，D∥AB，DF∥AC试说明∠FDE=∠A

解：

∵DE∥AB（）

∴∠A+∠AED=180０（）

∵DF∥AC（）

∴∠AED+∠FED=180０（）

∴∠A=∠FDE（）

练习题六：

1、如图1，已知直线AB∥CD，如果AB⊥MN，那么CD与MN垂直吗？

为什么？

如果EF也垂直于MN，那么AB与EF平行吗？

为什么？

如果AB∥EF，那么CD∥EF吗？

为什么？

2、如图2，当∠1=∠2时，AB与CD平行吗？

为什么？

3、如图3，如果AB∥CD，那么图中哪些角相等？

哪些角互补？

图1图2图3

4、如图4：

AD⊥BC，垂足为D，DE//BA。

则CDE与BAD的关系是_____（填“相等”、“互余”或“互补”）

5、已知：

如图5，1=2=B，EF∥AB。

求证3=C。

证明：

∵1=B（）

∴DE∥BC（）

∴2=C（）

∵EF∥AB（）

∴B=3（）

又∵2=B（）

∴3=C（）

4、平移

（1）平移的要素：

①平移的方向；

②平移的距离

（2）定义：

将一个图形沿某个方向移动叫做平移

（3）平移的性质：

①把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同。

②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点，连接各组对应点的线段平行且相等。

（4）平移的作图方法：

①找出已知图形上的关键点

②过这些点沿指定方向平移，平移距离等于已知距离

③依次作出各个对应点，连结所平移后的点得平移图形

例：

属于平移的有哪些？

答：

属于平移的有①，④

注意：

平移不改变图形的形状与大小，平移前与平移后的图形是全等形；因此平移是解决全等问题的一个重要方法

是添加辅助线的依据之一。

练习题七：

1、图形中的平行移动，简称平移，它由移动的（）所决定

A．方向B．距离C．方向和距离D．以上答案均不对

2、如图，四边形

沿着

方向，平移到四边形

，则点A的对应点是点____,点B的对应点是点_______,线段AB的对应线段是线段_________。

对应角是_______________,四边形

平移到______________，四边形

沿着___________方向平移到_________________。

3、如图,

________。

4、

（1）将线段AB向北偏东方向平移5cm，则点A平移方向__________，平移距离为____________

（2）经过平移后的图形与__________全等

5、下列物体运动中平移的是_________（填序号）

①打乒乓球的运动；②手表上指针的运动；③汽车在笔直公路上运动；④车轮的滚动

6、如图，经过平移,三角形ABC的边AB移到了EF,作出平移后的三角形,你能给出几种作法?

7、如图,将半圆图形按箭头所指的方向平移,其中A点到了A`点,作出平移后的图形.

8、如图,在四边形ABCD中,AD//BC,AB=CD,AD

平移后的三角形中,与B,E的对应点F,G,还是在BC边上吗?

∠B和∠C相等吗?

说明理由