哈工大机械原理凸轮大作业.docx
《哈工大机械原理凸轮大作业.docx》由会员分享,可在线阅读,更多相关《哈工大机械原理凸轮大作业.docx(15页珍藏版)》请在冰豆网上搜索。
哈工大机械原理凸轮大作业
一、题目要求及机构运动简图
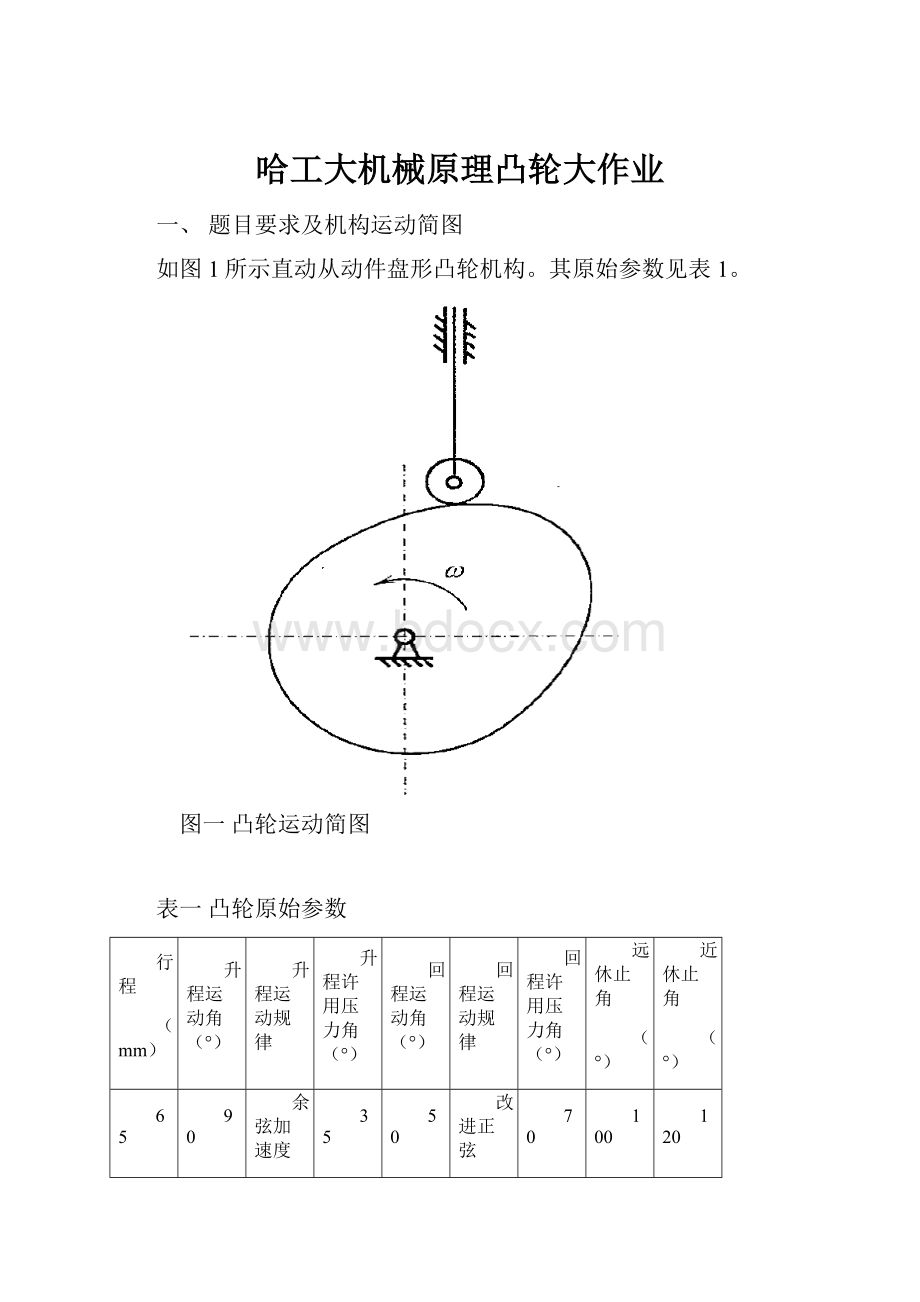
如图1所示直动从动件盘形凸轮机构。
其原始参数见表1。
图一凸轮运动简图
表一凸轮原始参数
行程
(mm)
升程运动角(°)
升程运动规律
升程许用压力角(°)
回程运动角(°)
回程运动规律
回程许用压力角(°)
远休止角
(°)
近休止角
(°)
65
90
余弦加速度
35
50
改进正弦
70
100
120
二、计算流程框图
三、建立数学模型
1.从动件运动规律方程
首先,由于设计凸轮轮廓与凸轮角速度无关,所以不妨设凸轮运动角速度为w=1rad/s。
(1)推程运动规律(0<φ<90°)
s=
v=
a=
式中:
h=65mm,Φ0=π/2
(2)远休程运动规律(90°<φ<190°)
s=65mm
v=0
a=0
(3)回程运动规律(190°<φ<240°)
(190°<φ<196.25°)
(196.25°<φ<233.75°)
(233.75°<φ<240°)
回程运动中的速度和加速度为位移对时间t的倒数:
(4)近休程运动规律(240°<φ<360°)
s=0
v=0
a=0
2.从动件位移、速度、加速度线图
(1)位移线图
(2)速度线图
(3)加速度线图
(4)位移、速度、加速度线图MATLAB源程序
%%已知条件
h=65;%mm
phi_0=90./180*pi;%rad
alpha_up_al=35./180*pi;%升程许用压力角
phi_00=50./180*pi;
alpha_down_al=70./180*pi;%回程许用压力角
phi_s=100./180*pi;
phi_ss=120./180*pi;
w=1;
%%绘制从动件位移、速度、加速度线图
%推程阶段
t_up=0:
0.5:
90;
t_up1=t_up./180*pi;
symst_up1phi_ups_upv_upa_up
phi_up=w.*t_up1;
s_up=h./2.*(1-cos(pi.*phi_up./phi_0));
v_up=diff(s_up,t_up1);
a_up=diff(v_up,t_up1);
s_up1=double(subs(s_up,t_up./180*pi));
v_up1=double(subs(v_up,t_up./180*pi));
a_up1=double(subs(a_up,t_up./180*pi));
%远休程
t_s=90:
0.5:
(90+100);
t_s1=t_up./180*pi;
s_s(1:
201)=h;
v_s(1:
201)=0;
a_s(1:
201)=0;
%回程阶段1
t_down1=(90+100):
0.5:
(90+100+50/8);
t_down11=t_down1./180*pi;
symst_down11phi_down1s_down1v_down1a_down1
phi_down1=w.*t_down11;
s_down1=h-h./(4+pi).*(pi.*(phi_down1-phi_0-phi_s)./phi_00-...
sin(4.*pi.*(phi_down1-phi_0-phi_s)./phi_00)./4);
v_down1=diff(s_down1,t_down11);
a_down1=diff(v_down1,t_down11);
s_down11=double(subs(s_down1,t_down1./180*pi));
v_down11=double(subs(v_down1,t_down1./180*pi));
a_down11=double(subs(a_down1,t_down1./180*pi));
%回程阶段2
t_down2=(90+100+50/8):
0.5:
(90+100+7*50/8);
t_down22=t_down2./180*pi;
symst_down22phi_down2s_down2v_down2a_down2
phi_down2=w.*t_down22;
s_down2=h-h./(4+pi).*(2+pi.*(phi_down2-phi_0-phi_s)./phi_00-9.*sin(pi./3+4.*pi.*(phi_down2-phi_0-phi_s)./(3.*phi_00))./4);
v_down2=diff(s_down2,t_down22);
a_down2=diff(v_down2,t_down22);
s_down22=double(subs(s_down2,t_down2./180*pi));
v_down22=double(subs(v_down2,t_down2./180*pi));
a_down22=double(subs(a_down2,t_down2./180*pi));
%回程阶段3
t_down3=(90+100+7*50/8):
0.5:
(90+100+50);
t_down33=t_down3./180*pi;
symst_down33phi_down3s_down3v_down3a_down3
phi_down3=w.*t_down33;
s_down3=h-h./(4+pi).*(4+pi.*(phi_down3-phi_0-phi_s)./phi_00-…
sin(4.*pi.*(phi_down3-phi_0-phi_s)./phi_00)./4);
v_down3=diff(s_down3,t_down33);
a_down3=diff(v_down3,t_down33);
s_down33=double(subs(s_down3,t_down3./180*pi));
v_down33=double(subs(v_down3,t_down3./180*pi));
a_down33=double(subs(a_down3,t_down3./180*pi));
%近休程
t_ss=(90+100+50):
0.5:
360;
s_ss(1:
241)=0;
v_ss(1:
241)=0;
a_ss(1:
241)=0;
%绘图位移
t=[t_upt_st_down1t_down2t_down3t_ss];
phi=w.*t./180.*pi;
s=[s_up1s_ss_down11s_down22s_down33s_ss];
v=[v_up1v_sv_down11v_down22v_down33v_ss];
a=[a_up1a_sa_down11a_down22a_down33a_ss];
figure('Name','从动件位移-时间线图');
plot(t,s,'k','linewidth',1.0);
gridon;
title('从动件位移-时间线图');
xlabel('转角\phi/度');
ylabel('位移h/mm');
%绘图速度
figure('Name','从动件速度-时间线图');
plot(t,v,'k','linewidth',1.0);
gridon;
title('从动件速度-时间线图');
xlabel('转角\phi/度');
ylabel('速度v/mm*s^{-1}');
%绘图加速度
figure('Name','从动件加速度-时间线图');
plot(t,a,'k','linewidth',1.0);
gridon;
title('从动件加速度-时间线图');
xlabel('转角\phi/度');
ylabel('加速度a/mm*s^{-2}');
3.绘制ds/dΦ线图并确定基圆半径和偏距
(1)绘制ds/dΦ线图及源程序
MATLAB源程序:
%%绘制ds/dphi-s线图,确定基圆半径和偏距
ds_dphi=v./w;
figure('Name','凸轮ds/dphi-s线图');
plot(ds_dphi,s,'k','linewidth',1.5);
holdon;
axis([-150150-7070]);
gridon;
title('凸轮ds/dphi-s线图');
xlabel('ds/dphi/(mm*s^{-2})');
ylabel('s/mm');
%三条临界线
x=linspace(-150,150,301);
k_up=tan(pi/2-alpha_up_al);
y_up=k_up.*x-66;
plot(x,y_up,'linewidth',1.5);
k_down=-tan(pi/2-alpha_down_al);
y_down=k_down.*x-24.7;
plot(x,y_down,'linewidth',1.5);
x0=linspace(0,150,151);
k0=-tan(alpha_up_al);
y0=k0.*x0;
plot(x0,y0,'--');
%由图像选取凸轮基圆半径为r0=sqrt(23^2+34^2)=41mm,偏距e=23mm
plot(23,-34,'or');
r0=41;
e=23;
plot(linspace(0,23,10),linspace(0,-34,10),'r',linspace(0,23,10),linspace(-34,-34,10),'r',linspace(23,23,10),linspace(0,-34,10),'r','linewidth',1.0);
(2)确定基圆半径和偏距
在凸轮机构的ds/dφ-s线图里再作斜直线Dt-dt与升程的[ds/dφ-s]曲线相切并使与纵坐标夹角为升程许用压力角[α],则Dt-dt线的右下方为选择凸轮轴心的许用区。
作斜直线Dt'-dt'与回程的[ds/dφ-s]曲线相切,并使与纵坐标夹角为回程的许用压力角[α],则Dt'-dt'线的左下方为选择凸轮轴心的许用区。
考虑到升程开始瞬时机构压力角也不超过许用值,自B0点作限制线B0-d0''与纵坐标夹角为升程[α],则这三条直线的围成的下方区域为为选取凸轮中心的许用区。
由图可取基圆半径r0=
=41mm,偏距e=23mm,s0=34mm。
4.绘制凸轮理论轮廓压力角、曲率半径线图
(1)压力角、曲率半径数学模型
压力角计算公式:
曲率半径计算公式:
其中:
(2)MATLAB程序
%%凸轮理论轮廓压力角和曲率半径线图
r0=41;
e=23;
s0=34;
%压力角
t=[t_upt_st_down1t_down2t_down3t_ss];
alpha=atan(abs(ds_dphi-e)./(s0+s))./pi.*180;
%曲率半径
p=((r0+s).^2+(w.*v).^2).^(3./2)./((r0+s).^2+2.*(w.*v).^2-w.*w.*a.*(r0+s));
%画图
figure('Name','凸轮理论轮廓压力角和曲率半径线图');
[hAx,hLine1,hLine2]=plotyy(t,p./2,t,alpha);
title('凸轮理论轮廓压力角和曲率半径线图');
xlabel('转角\phi/度');
ylabel(hAx
(1),'曲率半径*2/mm');%lefty-axis
ylabel(hAx
(2),'压力角/度');%righty-axis
gridon;
axis(hAx
(1),[0,360,-20,100]);
axis(hAx
(2),[0,360,-20,100]);
hLine1.LineWidth=1;
hLine2.LineWidth=1;
hLine1.Color='k';
hLine2.Color='b';
(3)理论轮廓压力角、曲率半径线图
5.确定滚子半径,绘制凸轮理论轮廓与实际轮廓
(1)建立数学模型
根据曲率半径线图可知,最小曲率半径在30mm附近,防止凸轮工作轮廓出现尖点或出现相交包络线,选取滚子半径为rr=10mm。
凸轮理论轮廓曲线方程为:
(其中
凸轮实际轮廓曲线方程为:
(其中
(2)MATLAB程序
%%确定滚子半径,绘制凸轮理论轮廓和实际轮廓
rr=10;%滚子半径
%理论轮廓
x=(s0+s).*sin(phi)+e.*cos(phi);
y=(s0+s).*cos(phi)-e.*sin(phi);
%实际轮廓
X=x+rr.*(gradient(y)./0.5)./sqrt((gradient(x)./0.5).^2+(gradient(y)./0.5).^2);
Y=y-rr.*(gradient(x)./0.5)./sqrt((gradient(x)./0.5).^2+(gradient(y)./0.5).^2);
%绘图
figure('Name','凸轮轮廓');
plot(x,y,'k',X,Y,'k','linewidth',1.0);%轮廓
holdon;
gridon;
theta=0:
pi/100:
2*pi;
plot(r0.*cos(theta),r0.*sin(theta),'k','linewidth',1.0);%基圆
plot((r0-rr).*cos(theta),(r0-rr).*sin(theta),'k','linewidth',1.0);
plot(e.*cos(theta),e.*sin(theta),'k');
plot(rr*cos(theta)+e,rr*sin(theta)+s0,'k','linewidth',1.0);%滚子
plot(e,s0,'Marker','o','MarkerSize',5,'MarkerFaceColor','k');
plot([e,e],[s0,s0+100],'k','linewidth',1.0);%从动件
plot([e-3,e-3],[100,110],'k','linewidth',1.0);
plot([e+3,e+3],[100,110],'k','linewidth',1.0);
axisequal;
title('凸轮轮廓');
xlabel('x/mm');
ylabel('y/mm');
(3)凸轮轮廓图
四、计算结果分析
根据位移、速度、加速度线图可知:
凸轮运动一个周期中,从动件的速度没有突变,但是加速度在推程阶段是有突变的,所以在推程阶段是柔性冲击的,该机构适用于低速和中速情况。
而且从动件回程阶段的速度要要达到了升程阶段的2倍,回程的时间也远小于升程的时间,这样大大提高了工作的效率。
根据曲率半径线图可知:
曲率半径的最小值为30mm,而滚子半径为10mm,所以曲率半径最小值要大于滚子半径,不会出现尖点。
根据压力角线图可知:
推程压力角的最大值为35度,等于许用推程压力角。
回程压力角的最大值为70度,也等于回程许用压力角。
所以该凸轮设计符合要求。