人教版小学数学五年级下册第七、八单元水平测试卷.doc

人教版小学数学五年级下册第七、八单元水平测试卷.doc

《人教版小学数学五年级下册第七、八单元水平测试卷.doc》由会员分享，可在线阅读，更多相关《人教版小学数学五年级下册第七、八单元水平测试卷.doc（2页珍藏版）》请在冰豆网上搜索。

人教版小学数学五年级下册第七、八单元水平测试卷2017-2018下

学校___________班级___________姓名__________成绩_______

一、先在下面折线统计图的括号里填入适当的数，然后根据折线统计图回

答问题。

（31分）

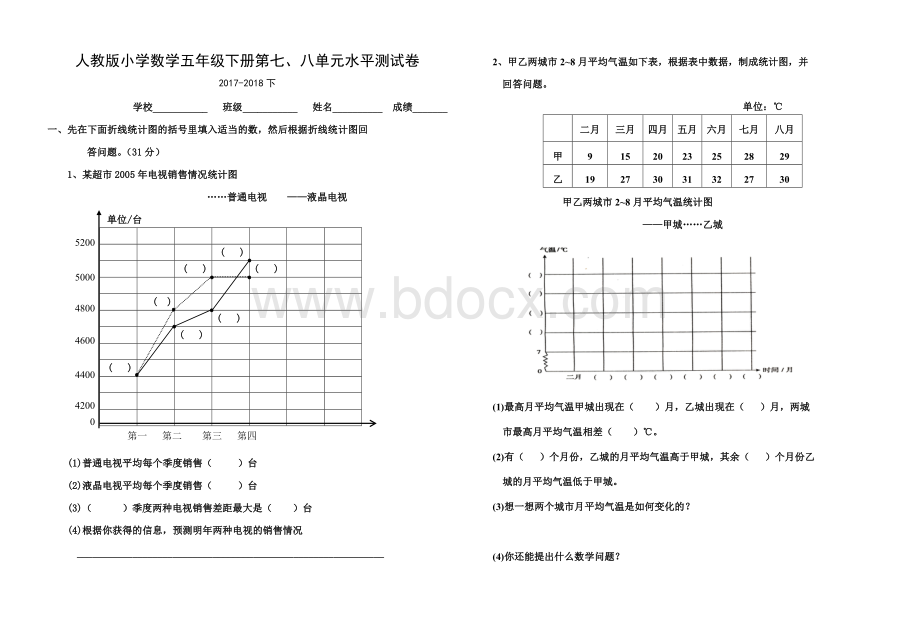
1、某超市2005年电视销售情况统计图

……普通电视——液晶电视

5200

5000

4800

4600

4400

4200

0

单位/台

（）

（）

（）

（）

（）

（）

（）

第一第二第三第四

（1）普通电视平均每个季度销售（）台

（2）液晶电视平均每个季度销售（）台

（3）（）季度两种电视销售差距最大是（）台

（4）根据你获得的信息，预测明年两种电视的销售情况

_____________________________________________________________

2、甲乙两城市2~8月平均气温如下表，根据表中数据，制成统计图，并

回答问题。

单位：

℃

二月

三月

四月

五月

六月

七月

八月

甲

9

15

20

23

25

28

29

乙

19

27

30

31

32

27

30

甲乙两城市2~8月平均气温统计图

——甲城……乙城

（1）最高月平均气温甲城出现在（）月，乙城出现在（）月，两城

市最高月平均气温相差（）℃。

（2）有（）个月份，乙城的月平均气温高于甲城，其余（）个月份乙

城的月平均气温低于甲城。

（3）想一想两个城市月平均气温是如何变化的？

（4）你还能提出什么数学问题？

二、口算（10分）

1.2×3=2.6×10=24÷0.8=1-=

0.4÷0.8=0.25÷0.5=3×2.7=+=

3.52-0.52=1.4×5=0.999×0=-=

4÷0.4=3.7+2.3=57÷5.7=+=

-=-=+=+=

三、选择题（39分）

1.要表示某地近几年7月平均气温的变化情况，应选用（）比较合适。

A．单式折线统计图B．复式折线统计图

C．单式条形统计图D．复式条形统计图

2.如果要统计出某县8个乡镇去年新生婴儿性别情况，应制成（）统计图更合适。

A．单式折线统计图B．复式折线统计图

C．单式条形统计图D．复式条形统计图

3.如果要统计出某县2009年至2016年，每年新生婴儿性别变化情况，应制成（）统计图更合适。

A．单式折线统计图B．复式折线统计图

C．单式条形统计图D．复式条形统计图

4.下面是科技小组的同学绘制的某日气温统计图。

从统计图中看出，科技小组的同学每隔（）小时测量一次气温。

（看图一）A．1B．2C．4D．8

（图一）（图二）

5.如图是某商店2006年下半年毛衣和衬衫销售情况统计图，毛衣的销售量在（）月最大，衬衫的销售量在（）月最大。

（看图二）

A.7；11B.11；7C.7；12D.12；7

6.下面是一辆汽车与一列火车的行程图表，根据图示回答：

汽车的速度是每分钟（）千米。

（看图三）A．0.6B．0.5C．0.7D．0.8

（图三）（图四）

7.下面是一辆汽车与一列火车的行程图表，根据图示回答：

火车停站时间是（）分钟。

（看图三）A．5B．8C．10D．15

8.下面是一辆汽车与一列火车的行程图表，根据图示回答：

汽车比火车早到（）分钟。

（看图三）A．5B．20C．10D．15

9.小林和小明骑自行车从学校沿着一条路线到20千米外的公园，已知小林比小明先出发，他们俩所行的路程和时间的关系如图所示。

下面说法正确的是（）。

（看图四）

A.他们都骑行了20千米B.两个人同时到达森林公园

C.小林在中途停留了1小时D.相遇后，小林的速度比小明慢

10.有8瓶饮料，其中有一瓶多装了4毫升。

用天平称，至少称（）次能保证找出这瓶多4毫升的饮料。

A．2B．3C．4D.5

11.有7个零件，其中有1个零件是次品（次品轻一些）。

用天平称，如果天平每边各放3个，称1次（）找出这个次品。

A．一定能够B．不能C．可能

12.用天平从20个零件中找一个稍轻的次品，与从27个零件中找一个稍轻的次品，要保证找出来，（）。

A．从20个里找用的次数少些B．从27个里找用的次数少些

C．用的次数一样多D.不能确定

13.有26枚金币，其中一枚是假的（假金币轻一些）。

第—次用天平称，方法（）最好。

A．天平左右两边各放10枚，旁边放6枚。

B．天平左右两边各放8枚，旁边放10枚

C．天平左右两边各放9枚，旁边放8枚D.不能确定

四、解决问题。

（20分）

1、有5瓶钙片，其中1瓶少了3片，用天平称，至少称几次就一定能找

出来？

2、有15盒饼干，其中的14盒质量相同，另有1盒少了几块，如果有天

平称，至少几次可以找出这盒饼干？