通信原理与信号系统学习指南.docx
《通信原理与信号系统学习指南.docx》由会员分享,可在线阅读,更多相关《通信原理与信号系统学习指南.docx(18页珍藏版)》请在冰豆网上搜索。
通信原理与信号系统学习指南
开场:
很多原理一旦上升为理论,常常伴随着繁杂的数学推导,很简单的本质反而被一大堆公式淹没,通信原理因此让很多人望而却步。
非常复杂的公式背后很可能隐藏了简单的道理。
真正学好通信原理,关键是要透过公式看本质。
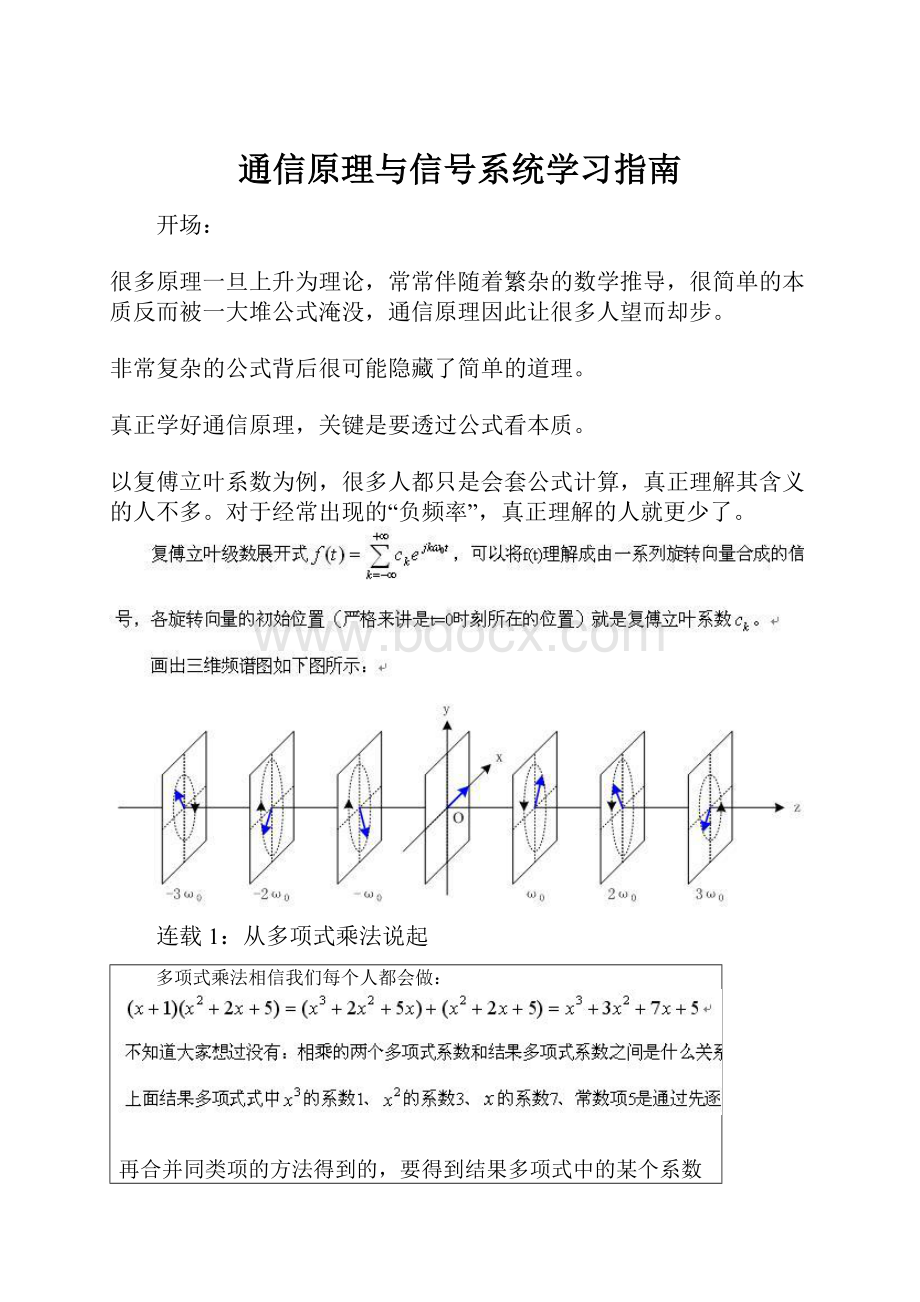
以复傅立叶系数为例,很多人都只是会套公式计算,真正理解其含义的人不多。
对于经常出现的“负频率”,真正理解的人就更少了。
连载1:
从多项式乘法说起
多项式乘法相信我们每个人都会做:
再合并同类项的方法得到的,要得到结果多项式中的某个系数,需要两步操作才行,有没有办法一步操作就可以得到一个系数呢?
下面的计算方法就可以做到:
这种计算方法总结起来就是:
反褶:
一般多项式都是按x的降幂排列,这里将其中一个多项式的各项按x的升幂排列。
平移:
将按x的升幂排列的多项式每次向右平移一个项。
相乘:
垂直对齐的项分别相乘。
求和:
相乘的各结果相加。
反褶、平移、相乘、求和-这就是通信原理中最常用的一个概念“卷积”的计算过程。
连载2:
卷积的表达式
利用上面的计算方法,我们很容易得到:
c(0)=a(0)b(0)
c
(1)=a(0)b
(1)+a
(1)b(0)
c
(2)=a(0)b
(2)+a
(1)b
(1)+a
(2)b(0)
c(3)=a(0)b(3)+a
(1)b
(2)+a
(2)b
(1)+a(3)b(0)
其中:
a(3)=a
(2)=b(3)=0
在上面的基础上推广一下:
假定两个多项式的系数分别为a(n),n=0~n1和b(n),n=0~n2,这两个多项式相乘所得的多项式系数为c(n),则:
c(0)=a(0)b(0)
c
(1)=a(0)b
(1)+a
(1)b(0)
c
(2)=a(0)b
(2)+a
(1)b
(1)+a
(2)b(0)
c(3)=a(0)b(3)+a
(1)b
(2)+a
(2)b
(1)+a(3)b(0)
c(4)=a(0)b(4)+a
(1)b(3)+a
(2)b
(2)+a(3)b
(1)+a(4)b(0)
以此类推可以得到:
上面这个式子就是a(n)和b(n)的卷积表达式。
通常我们把a(n)和b(n)的卷积记为:
a(n)*b(n),其中的*表示卷积运算符。
连载3:
利用matlab计算卷积
表面上看,卷积的计算公式很复杂,计算过程也很麻烦(反褶,平移,相乘,求和),实际上使用Matlab很容易计算。
以上面的a(n)=[11],b(n)=[125]的卷积计算为例:
>>a=[11];
>>b=[125];
>>c=conv(a,b);
>>c
c=
1375
后面很多地方的讲解都会用到matlab,没用过matlab的同学,请到网上下载个matlab7.0,安装后,将上面前4行内容拷贝到命令窗口中执行,即可得到上面的执行结果。
为了更好地理解卷积(多项式相乘,相当于系数卷积),我们用matlab画一下高中学过的杨辉三角。
杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
1
11
121
1331
14641
15101051
1615201561
其中每一横行都表示(a+b)^n(此处n=1,2,3,4,5,6,∙∙∙∙∙∙)展开式中的系数。
杨辉三角最本质的特征是,它的两条斜边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和。
>>x=[11];y=[11];
>>y
y=
11
>>y=conv(x,y)
y=
121
>>y=conv(x,y)
y=
1331
>>y=conv(x,y)
y=
14641
>>y=conv(x,y)
y=
15101051
>>y=conv(x,y)
y=
1615201561
连载4:
将信号表示成多项式的形式
多项式乘法给了我们启发:
如果信号可以分解为类似多项式的这种形式:
存不存在满足这个条件的x呢?
前人早就给出了答案,那就是:
附:
前面推导过程中用到的几个三角公式:
连载5:
著名的欧拉公式
这就是著名的欧拉公式。
对于欧拉公式,大家知道结论就可以了,想知道怎么得来的同学请参考下面的证明。
欧拉公式的证明(利用泰勒级数展开):
连载6:
利用卷积计算两个信号的乘积
下面我们举个具体的例子来体会一下“如果信号可以分解为类似多项式的这种形式:
会涉及一系列的三角函数公式,计算过程非常麻烦。
具体的计算过程这里就不列了,大家可以试一下,看看有多麻烦。
连载7:
信号的傅立叶级数展开
上面这种把信号表示成形式类似于多项式的方法,本质上就是傅里叶级数展开,多项式中各项的系数实际就是傅里叶系数:
以频率为横轴,傅里叶系数为纵轴,画出的图就是频谱图。
前面我们已经知道:
[3,17,28,12]=[1,5,6]*[3,2]
因此很容易得出:
时域相乘,相当于频域卷积。
连载8:
时域信号相乘相当于频域卷积
连载9:
用余弦信号合成方波信号
前面为了利用卷积,我们将信号表示成了多项式的形式,用多个复指数信号合成我们所需的信号。
为了更好地理解多个复指数信号合成所需信号,我们先来看一下用多个余弦信号合成方波信号的过程。
直流分量叠加一个cos(x)余弦分量:
y=0.5+0.637.*cos(x);
再叠加一个cos(3x)余弦分量:
y=0.5+0.637.*cos(x)-0.212.*cos(3*x);
再叠加一个cos(5x)余弦分量:
y=0.5+0.637.*cos(x)-0.212.*cos(3*x)+0.127.*cos(5*x);
随着合成的余弦信号越来越多,波形越来越逼近一个方波,这从一个侧面验证了傅立叶级数展开的正确性:
可以将方波分解成一个直流分量和无数个余弦波分量之和。
连载10:
傅立叶级数展开的定义
连载11:
如何把信号展开成复指数信号之和?
前面我们已经把信号展开成了直流分量、余弦分量和正弦分量之和,可是如何把信号展开成复指数信号之和呢?
将上述公式代入前面的傅立叶级数展开式中,我们就可以得到一个很简洁的复指数形式的傅立叶展开式。
建议大家动手推导推导,这样可以加深印象。
其中:
连载12:
复傅立叶系数
连载13:
实信号频谱的共轭对称性