第二章核心理论基础.docx
《第二章核心理论基础.docx》由会员分享,可在线阅读,更多相关《第二章核心理论基础.docx(19页珍藏版)》请在冰豆网上搜索。
第二章核心理论基础
第二章无图纸设计与制造技术理论基础
2.1三维几何建模
建模技术是将现实世界中的物体及其属性转化为计算机内部以数字化表达的原理和方法,是定义产品在计算机内部表示的数字模型和图形信息的工具,它为后续的产品设计分析、虚拟装配及干涉分析、数控加工编程及仿真加工和生产过程管理等提供了有关产品信息描述和表达方法,是实现无图纸设计与制造技术的前提条件。
本节将讨论与曲线曲面建模和实体建模等三维几何建模相关的原理和方法。
2.1.1计算机内部表示与建模
1)计算机内部表示与建模的基本含义
所谓计算机内部表示,就是决定在计算机内部采用什么样的数字化模型来描述、存储和表达现实世界中的物体。
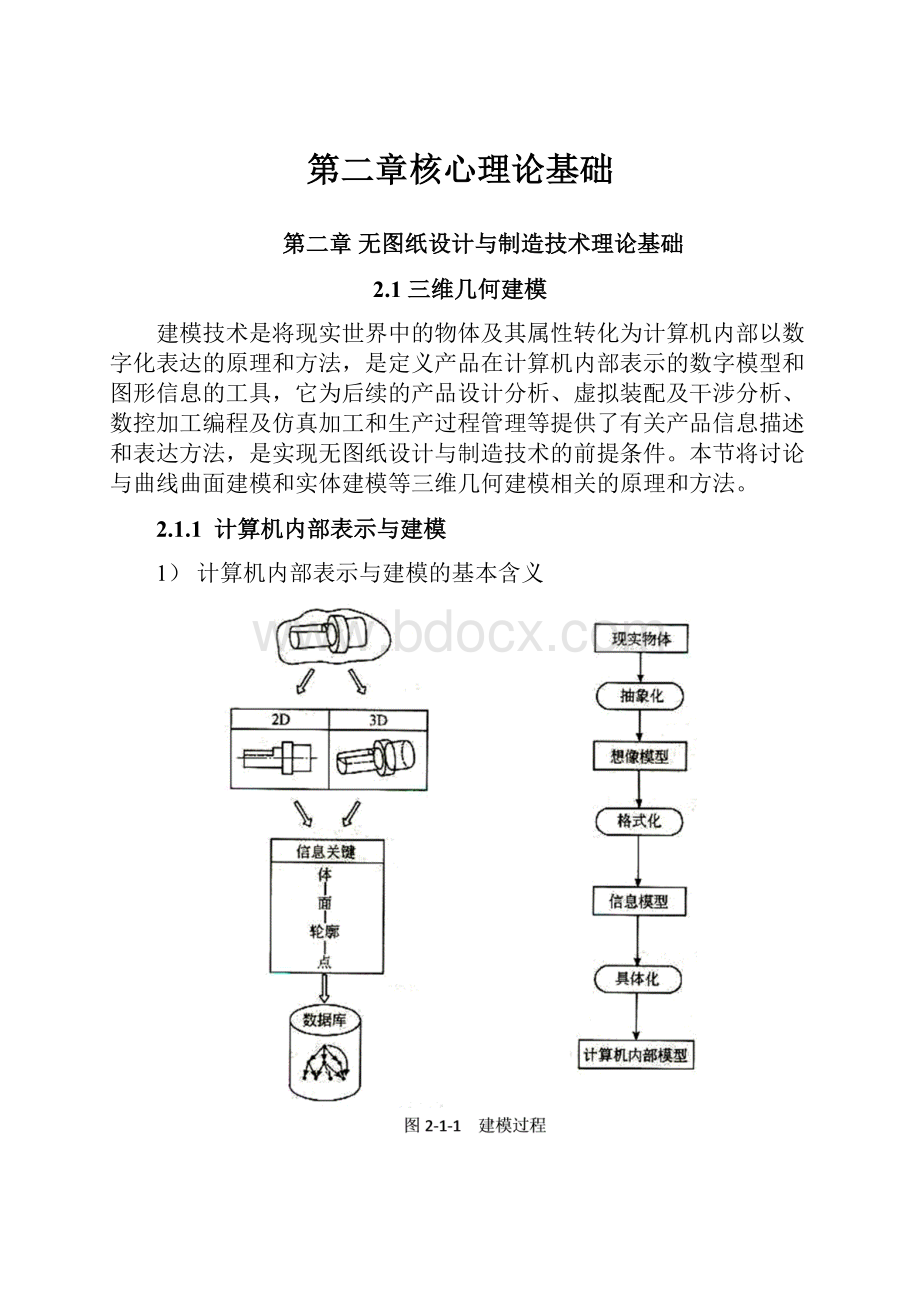
对于现实世界中的物体,从人们的想象出发,到完成它的计算机内部表示这一过程称之为建模。
建模的一般步骤如图2-1-1所示。
在传统的产品开发中,设计人员通过绘制工程图来表达和传递设计思想及工程信息。
应用计算机辅助技术后,这些设计思想和工程信息是以具有一定结构的数字化模型方式存储在计算机内,并经过适当转换提供给生产过程各个环节,从而构成统一产品数据模型。
而模型一般是由数据、结构和算法三部分组成。
所以建模技术就是研究产品数据模型在计算机内部的建立方法过程及采用的数据结构和算法。
目前,计算机建模的主要方法有几何建模和特征建模两种。
几何建模经过几十年的发展已非常成熟,大部分CAD/CAM系统采用的都是几何建模方法,因此本节只从几何建模角度来阐述建模过程中的理论及实现。
2)几何建模
所谓CAD/CAM系统中的几何建模就是把三维实体的几何形状及其属性用合适的数据结构进行描述和存储,供计算机进行信息转换与处理的数据模型。
该模型包含了三维形体的几何信息、拓扑信息以及其它的属性数据。
而所谓的几何建模实际上就是用计算机及其图形系统来表示和构造形体的几何形状,建立计算机内部模型的过程。
3)几何建模系统的分类
根据不同的应用场合和目的,几何建模系统可以分为二维几何建模系统和三维几何建模系统两大类。
二维几何建模系统主要研究平面轮廓处理问题,可以满足一般二维绘图工作的要求,但缺乏直观性及表达不完整,而且也很难描述复杂曲面形状。
三维几何建模系统克服了二维几何建模系统的不足,可更加真实、完整、清楚地描述物体。
三维几何建模系统分为线框建模、表面建模和实体建模三类。
2.1.2三维几何建模
1)三维线框建模
三维线框建模是最早应用的三维几何建模方法。
线框模型在计算机内部是以边表、点表来描述和表达物体的。
例如图2-1-2所示的物体在计算机内部是通过12个点和18条边来表达线框模型的。
这种描述方法所需信息量最少,因此具有数据结构简单、对硬件要求不高、显示响应速度快等优点。
但可从图中看出,边与边之间没有关系,即没有构成关于面的信息,因此不存在内、外表面的区别,甚至存在多义性。
另外由于没有面的概念,无法识别可见边,也就不能自动进行可见性检验及消隐。
由此可见,线框模型不适用于对物体需要进行完整信息描述的场合。
但是在有些情况下,例如评价物体外部形状、布局、干涉检验或绘制图纸等,线框模型提供的信息己经足够;同时由于它具有较好的时间响应特性,所以对于实时仿真技术或中间结果显示很适用。
在实体建模的CAD系统中常采用线框模型显示中间结果。
2)曲面建模
曲面建模,即表面建模(SurfaceModeling),是通过对物体的各种表面或曲面进行描述的一种三维建模方法,主要适用于其表面不能用简单的数学模型进行描述的复杂物体型面,如:
汽车、飞机、家用电器等产品外观设计,如图2-1-3所示。
这种建模方法的重点是由给出的离散点数据构成光滑过渡的曲面,使这些曲面通过或逼近这些离散点。
目前应用最广泛的是双参数曲面,它仿照参数曲线的定义,将参数曲面看成是一条变曲线t=t(u)按某参数v运动形成的轨迹。
目前较为流行的几种参数曲线、曲面有:
贝赛尔(Bezier)、B样条、孔斯(Coons)、非均匀有理B样条(NURBS)等。
(1)贝赛尔(Bezier)曲线、曲面:
它是法国雷诺汽车公司的Bezier在1962提出的一种构造曲线、曲面的方法。
图2-1-4(a)所示为三次Bezier曲线的形成原理,这是由4个位置矢量Q0、Q1、Q2、Q3定义的曲线。
通常将Q0、Q1、……Qn组成的多边形折线称为Bezier控制多边形。
多边形的第一条折线和最后一条折线代表曲线起点、终点的切线方向,其它顶点用于定义曲线的阶次和形状。
Bezier曲线的一般数学表达式为:
式中Qi为各顶点的位置矢量,Bi,n(t)为Bernstein基函数,由下式表示
当n=3时,公式2-1变为
或改成矩阵形式有
此式称为三次Bezier曲线。
三次Bezier曲线具有直观、使用方便,便于交互设计等优点,是应用最广泛的曲线。
但Bezier曲线和定义它的特征多边形有时相差甚远,同时当修改一个顶点或改变顶点数量时,整条曲线形状都会发生变化,所以曲线局部修改性比较差。
此外,高次Bezier曲线还有些理论问题待解决,所以通常都是用分段的三次Bezier曲线来代替。
用一个参数t描述的向量函数可以表示一条空间曲线,用两个参数u、v描述的向量函数就能表示一个曲面。
可以直接由三次Bezier曲线的定义推广到双三次Bezier曲面的定义。
图2-1-4(b)中有4条Bezier曲线Pi(u),(i=0,1,2,3),它们分别以Qi,j为控制顶点(j=0,1,2,3)。
当4条曲面的参数u=u*时,形成4点P0(u*)、P1(u*)、P2(u*)、P3(u*),这4点构成Bezier曲线方程为:
当u*从0~1发生变化时,P(u*,v)为一条运动曲线,构成的曲面方程为
即为双三次Bezier曲线方程,写成矩阵形式为
式中,
(2)B样条曲线、曲面与Bezier曲线、曲面密切相关,它继承了Bezier曲线直观性好等优点,仍采用特征多边形及权函数定义曲线,B样条曲线方程为:
其中,di(i=0,1,…,n)为控制顶点,Ni,k(t)(i=0,1,…,n)称为k次规范B样条基函数,
为了便于推导,下面用另外一种形式来表达B样条的基函数:
式中,i是基函数的序号,i=0,1,2,…,n;n是样条次数;j表示一个基函数是由哪几项相加。
例如将n=3代入式(2-8)中得
因此,三次B样条曲线的矩阵表达式为
B样条曲线与特征多边形相当接近,同时便于局部修改。
与Bezier曲面生成过程相似。
由B样条曲线也很容易推广到B样条曲面,如图2-1-5所示的特征网络,它是由16个顶点Pij(i,j=0,1,2,3)惟一确定的双三次B样条曲面片,曲面方程为:
推广到任意次B样条曲面,设一组点Pij(i=0,1,2,…,n;j=0,1,2,…,m),有通用B样条曲面方程为
B样条方法比Bezier方法更具一般性,同时B样条曲线、曲面具有局部可修改性和很强的凸包性,因此较成功地解决了自由型曲线、曲面描述的问题。
(3)非均匀有理B样条(non-uniformrationalB-spline,NURBS)曲线、曲面:
这是一种能够将曲面实体溶为一体的表示方法,NURBS曲线提供了对标准解析几何和自由曲线、曲面的统一数学描述方法。
它可通过调整控制顶点和权因子,方便地改变曲面形状,同时也可方便地转换成对应的贝赛尔曲线,因此NURBS法己成为当前曲线、曲面建模中最为流行的技术。
STEP产品数据交换标准也将NURBS作为曲面几何描述的惟一方法。
NURBS曲线定义如下:
给定n+1个控制点Pi(i=0,1,…,n)及权因子Wi(i=0,1,…,n),则k阶(k-1)次NURBS曲线表达式为
其中,
为非均匀B样条基函数,按照deBoor-Cox公式递推地定义
NURBS曲面的定义与NURBS曲线的定义相似,给出一张(m+1)(n+1)的网络控制点Pij(i=0,1,2,…,n;j=0,1,2,…,m),以及各网络控制点的权值Wij(i=0,1,2,…,n;j=0,1,2,…,m),则其NURBS曲面的表达式为
式中,Ni,k(u)为NURBS曲面u参数方向的B样条基函数;Nj,l(v)为NURBS曲面v参数方向的B样条基函数;k,l为B样条基函数的阶次。
3)实体建模
实体建模(SolidModeling)是利用一些基本体素,如长方体、圆柱体、球体、锥体、圆环体以及扫描体等通过布尔运算生成复杂形体的一种建模技术。
实体建模主要包括两部分内容:
体素的定义及描述和体素之间的布尔运算(并、交、差)。
实体建模技术是20世纪70年代末期逐渐发展完善并推向市场的,并已成为目前CAD/CAM技术发展的主流。
(1)体素的定义及描述:
体素是现实生活中真实的三维实体。
体素的定义及描述有两种方法:
一种为基本体素,可通过少量参数进行描述,例如长方体通过长、宽、高定义,以及定义基本体素在空间的位置和方向。
在这里,基准点的定义很重要。
就长方体而论,它的基准点可位于它的一个顶点。
也可位于一个平面的中心。
不同的实体建模系统,可提供不同的基本体素类型。
图2-1-6为常见的基本体素。
另一种体素为平面轮廓扫描体,即平面轮廓扫描法生成的体素。
平面轮廓扫描法是一种与二维系统密切结合的、并常用于诸如棱柱体或回转体等生成的一种描述方法。
这种方法的基本设想是一个二维轮廓在空间平移或旋转就会扫描出一个实体。
由此扫描的前提条件是要有一个封闭的平面轮廓。
这一封闭的平面轮廓沿着某一个坐标方向移动或绕某一给定的轴旋转,便形成了如图2-1-7所示的两种扫描变换。
除了平面轮廓扫描外,还可以进行整体扫描。
所谓整体扫描就是使一个刚体在空间运动以产生新的物体形状。
这种方法在生产过程的模拟及干涉检验方面具有很大的实用价值。
特别是在NC加工中刀具路径生成和检验方面具有重要意义。
(2)布尔运算:
两个或两个以上体素经过集合运算得到实体的表示称为布尔模型(BooleanModel),这种集合运算称为布尔运算。
例如A、B两个实体经布尔运算生成C实体,那么布尔模型表示为:
C=AB,符号是布尔算子,它可以是“∪(并)”、“∩(交)”和“-(差)”等。
布尔模型是个过程模型,它通常可以直接以二叉树结构表示。
由于实体建模具有一系列优点,所以在设计与制造中广为应用。
尤其在运动学分析、干涉检验、五坐标NC铣削仿真和空间技术等方面已成为不可缺少的工具。
(3)三维实体模型的计算机内部表示方法:
现实世界中的物体是三维的连续实体,但计算机内部表示是一维的离散描述,如何利用一维离散来描述现实世界的三维实体、并保证数据的准确性、完整性、统一性,是计算机内部表示方法研究的内容。
目前,常见的计算机内部表示三维实体模型的方法有边界表示法、构造立体几何法、前两者的混合模式法、空间单元表示法和半空间法。
①边界表示法(BoundaryRepresentation,BRep)的基本思想是把物体定义为封闭的边界表面围成的有限空间,这样一个形体可通过它的边界,即面的子集来表示。
而每一个面又通过边、边通过点、点又通过3个坐标值来定义。
因此边界表示法强调的是形体外表细节,详细记录了构成几何形体的所有几何、拓扑信息,其模型中的数据结构呈如图2-1-8所示的网状关系。
这种内部结构和关系是与采用的物体生成描述方法无关的。
边界表示法的优点在于含有较多的关于面、边、点及其相互关系的信息,这些信息对于工程图绘制及图形显示都是十分重要的,并且易于同二维绘图软件衔接和同曲面建模软件联合应用。
此外,这种方法便于通过人机交互方式对物体模型进行局部修改。
但是有关物体生成的原始信息,即它是由哪些基本体定义的,是怎样拼合而成的,在边界表示法中无法提供,同时描述所需信息量较大,并有信息冗余。
②构造立体几何法(ConstructiveSolidGeometry,CSG)是通过基本体素及它们的集合运算(如并、交、差)进行表示的,即通过布尔模型生成二叉树结构进行表示,如图2-1-9所示。
从图2-1-9可以看出,同一物体可通过两种完全不同的CSG结构描述。
图2-1-9(a)所示是由两个长方体相加,而图2-1-9(b)所示是从大的长方体中减去小的长方体,两者不仅应用的布尔运算不同,而且采用的基本体素也不同。
CSG法强调的是记录各体素进入拼合时的原始状态,而BRep法则强调记录拼合后的结果。
CSG法的数据结构大部分是树状结构,叶结点为基本体素或变换矩阵,中间结点为布尔运算,根结点为物体的数字化模型。
出于这种数据结构的特点,它不可能存储最终物体更详细的几何信息,这是一种隐式模型。
如果需要,必须根据CSG结构进行推算。
这种推算过程是相当费时的,因此CSG模型几乎很少用到,常用的是混合模型,它是在CSG系统基础上发展起来的。
③混合模式(HybridModel)通常由两种不同的数据结构组成,例如在CSG树的结点上扩充一级边界数据结构,可以互相补充,达到实现快速图形显示的目的。
如图2-1-10所示。
目前该方法己经在CAD系统中得到广泛应用。
④空间单元法是通过一系列空间单元构成的图形来表示物体的一种方法。
空间单元模型的计算机内部表示常采用4叉树(Quldtree)和8叉树(Octtree)结构,如图2-1-11和图2-1-12所示。
其中4叉树用于二维物体描述,8叉树用于三维物体描述。
4叉树的基本设想是将平面划分为4个区域,也称为4个子平面,这些子平面仍可以继续划分。
通过定义这些子平面的“有图形”和“无图形”来描述不同形状的物体。
8叉树的基本设想是将空间通过三个坐标系由XY、XY、ZX划分为8个子空间(或称卦限)。
8叉树中的每一个结点对应着每一个子空间。
8叉树法的最大优点是便于作出局部修改及进行集合运算。
另外8叉树数据结构可大大简化消隐算法。
采用8叉树法最大的缺点是占用存储空间大。
2.2数控编程
数控编程经历了手工编程、APT语言自动编程和图形交互式自动编程3个阶段。
相对于手工编程和APT语言自动编程,图形交互式自动编程具有速度快、精度高、直观性好、使用简便、便于检查和修改等优点,已成为目前国内外数控加工普遍采用的数控编程方法。
本节主要介绍图形交互式自动编程的原理、实现过程和刀位点计算原理。
2.2.1图形交互式自动编程的原理和实现过程
1)原理
交互式图形编程是一种CAD/CAM集成的自动编程系统,它是以CAD技术为前提,利用CAD生成的三维实体模型,采用人机交互方式,在计算机屏幕上指定加工表面,并制订工艺方案,设置切削用量和切削方式等参数,系统就可自动计算并生成刀轨文件,然后通过后处理生成指定机床和数控系统的NC程序。
2)实现过程
图形交互式自动编程的基本实现过程及内容如图2-2-1所示。
(1)获得CAD模型
CAD模型是图形交互式自动编程的前提和基础。
获得CAD模型的方法通常有以下2种:
a)直接获取:
如果模型是在同一个CAD/CAM系统中建立的,则CAM模块可直接以内部统一的数据格式直接从CAD模块获取产品几何模型。
b)间接获取:
如果模型是由其它的CAD/CAM系统中建立的,则需要先将CAD模型转换成中性格式的文件,再输入到CAM系统中。
(2)加工工艺分析和规划
加工工艺分析和规划的水平原则上决定了NC程序的质量,主要包括下面几个方面的内容:
a)加工对象的确定:
通过对CAD模型的分析,确定哪些部位需要加工;
b)加工区域规划:
即对加工对象进行分析,按其形状特征、功能特征及精度、粗糙度要求将加工对象分成若干个加工区域。
对加工区域进行合理规划可以达到提高加工效率和加工质量的目的;
c)加工工艺路线规划:
即从粗加工到精加工再到清根加工的流程及加工余量分配;
d)加工工艺和加工方式确定:
如刀具选择、加工工艺参数和切削方式(刀轨形式)选择等。
(3)CAD模型完善
由于CAD设计人员更多考虑零件设计的方便性和完整性,很少顾及对CAM加工的影响,所以还要根据加工对象的确定及加工区域规划对模型作一些完善。
通常有以下内容:
a)坐标系的确定。
坐标系是加工的基准,将坐标系定位于适合机床操作人员确定的位置,同时保持坐标系的统一;
b)修补部分曲面。
对于间接获取的CAD模型,由于转换过程中难免会产生破孔等缺陷,需要将这些曲面重新修补完整,以使获得的刀轨更加规范和安全;
c)构建刀轨限制边界。
对于规划的加工区域,需要使用边界来限制加工范围的,应先构建出边界曲线。
(4)参数设置
参数设置可视为对工艺分析和规划的具体实施,它构成了利用CAD/CAM软件进行图形交互式自动编程的主要操作内容,直接影响着NC程序的生成质量。
参数设置的内容较多,主要包括:
a)切削方式设置:
用于指定刀轨的类型及相关参数;
b)加工对象设置:
是指用户通过交互手段选择被加工的几何体或其中的加工区域、毛坯、避让区域等;
c)刀具及机械参数设置:
针对每一道加工工序选择合适的加工刀具,并在CAD/CAM软件中设置相应的机械参数,包括主轴转速、进给率、切削液控制等;
d)加工程序参数设置:
包对进/退刀位置及方式、切削用量、步距、步长、加工余量、安全平面等。
这是参数设置中最主要的一部分内容。
(5)刀轨计算
在完成参数设置后,即可将设置结果提交给CAD/CAM系统进行刀轨的计算,其核心是刀位点的计算,其计算原理将在下面介绍。
(6)刀轨检验和后处理
刀轨检验和后处理的内容将在第十一章介绍。
2.2.2刀位点计算原理
数控编程的主要任务是计算刀轨,它是由一系列刀位点连接而成的折线,因此数控编程的核心内容就是计算刀轨上的刀位点。
下面简单介绍数控编程刀位点的计算原理。
数控加工刀位点的计算过程可分为三个阶段。
1)加工表面的偏置。
如图2-2-2所示,刀位点是刀具参考点的移动位置,它与加工表面存在一定的偏置关系。
这种偏置关系取决于刀具的形状和大小。
例如,当刀具半径为R的球头铣刀时,刀轨应当在距离加工表面为R的偏置面上,如图2-2-2所示。
由此可见,刀位点计算的前提是首先根据刀具的类型和尺寸计算出加工表面的偏置面。
2)刀轨形式的确定。
把刀位点在偏置面上的分布形式称为刀轨形式。
图2-2-3和图2-2-4所示是两种最常见的刀轨形式。
其中图2-2-3为行切刀轨,即所有刀位点都分布在一组与刀轴(Z轴)平行的平面内。
图2-2-4为等高线刀轨(又称环切刀轨),即所有刀位点都分布在与刀轴(Z轴)垂直的一组平行平面内。
显然,对于这两种刀轨来说,其刀位点分布在加工表面的偏置面与一组平行平面的交线上,这组交线称为理想刀轨,平行平面的间距称为刀轨的步距。
也就是说,刀轨形式一旦确定下来,就能够在加工表面的偏置面上以一定步距计算出理想刀轨。
3)刀位点的计算。
如果刀具中心能够完全按照理想刀轨运动的话,其加工精度无疑将是最理想的。
然而,由于数控系统通常只能完成直线和圆弧线的插补运动,因此只能在理想刀轨上以一定间距计算出刀位点,在刀位点之间做直线或圆弧运动,如图2-2-5所示。
刀位点的间距称为刀轨的步长,其大小取决于编程允许误差。
编程允许误差越大,则刀位点的间距越大;反之越小。
以上描述的仅仅是刀位点计算的基本思路,而CAM软件中实际采用的计算方法要复杂得多,而且随着软件的不同会有许多具体的变化。
但是不管是哪种CAM软件,其技术核心的共同点为:
即以一定的形式和密度在被加工面的偏置面上计算出刀位点。
刀位点的密度不仅指刀轨的步距,还指刀轨的步长,它们是影响数控编程精度的主要因素。
小结
本章主要介绍了在无图纸设计与制造技术中与三维几何建模和数控编程相关的理论和方法,包括图形的计算机内部表示和几何建模的概念及分类,曲线曲面、实体的数据结构和算法,图形交互式数控编程的理论和流程,以及刀位点计算原理等内容。
习题
1、回答下列问题:
1)三维几何建模有哪几种类型?
2)贝赛尔曲线、曲面有哪些优缺点?
3)贝赛尔、B样条和NURBS曲线曲面有何异同?
4)实体模型的计算机内部表示有哪几种方法?
各有何优缺点?
5)图形交互式编程的实现过程包括哪些内容?
6)刀位点的计算原理?