第X章 MATLAB在拟合与插值中的应用.docx
《第X章 MATLAB在拟合与插值中的应用.docx》由会员分享,可在线阅读,更多相关《第X章 MATLAB在拟合与插值中的应用.docx(15页珍藏版)》请在冰豆网上搜索。
第X章MATLAB在拟合与插值中的应用
MATLAB在拟合与插值中的应用
在大量的应用领域中,人们经常面临用一个解析函数描述数据(通常是测量值)的任务。
(比如在土木工程中对实验梁的应力应变(σ--ε)曲线的数据进行拟合,从而得出钢筋混凝土的弹性模量的计算式。
)在这里讨论的方法是曲线拟合与插值。
其中包括曲线拟合,一维插值,二维插值以及如何解决插值中求值时的单调性问题。
曲线拟合
曲线拟合涉及回答两个基本问题:
最佳拟合意味着什么?
应该用什么样的曲线?
可用许多不同的方法定义最佳拟合,并存在无穷数目的曲线。
我们将最佳拟合解释为在数据点的最小误差平方和,且所用的曲线限定为多项式时,那么曲线拟合是相当简捷的。
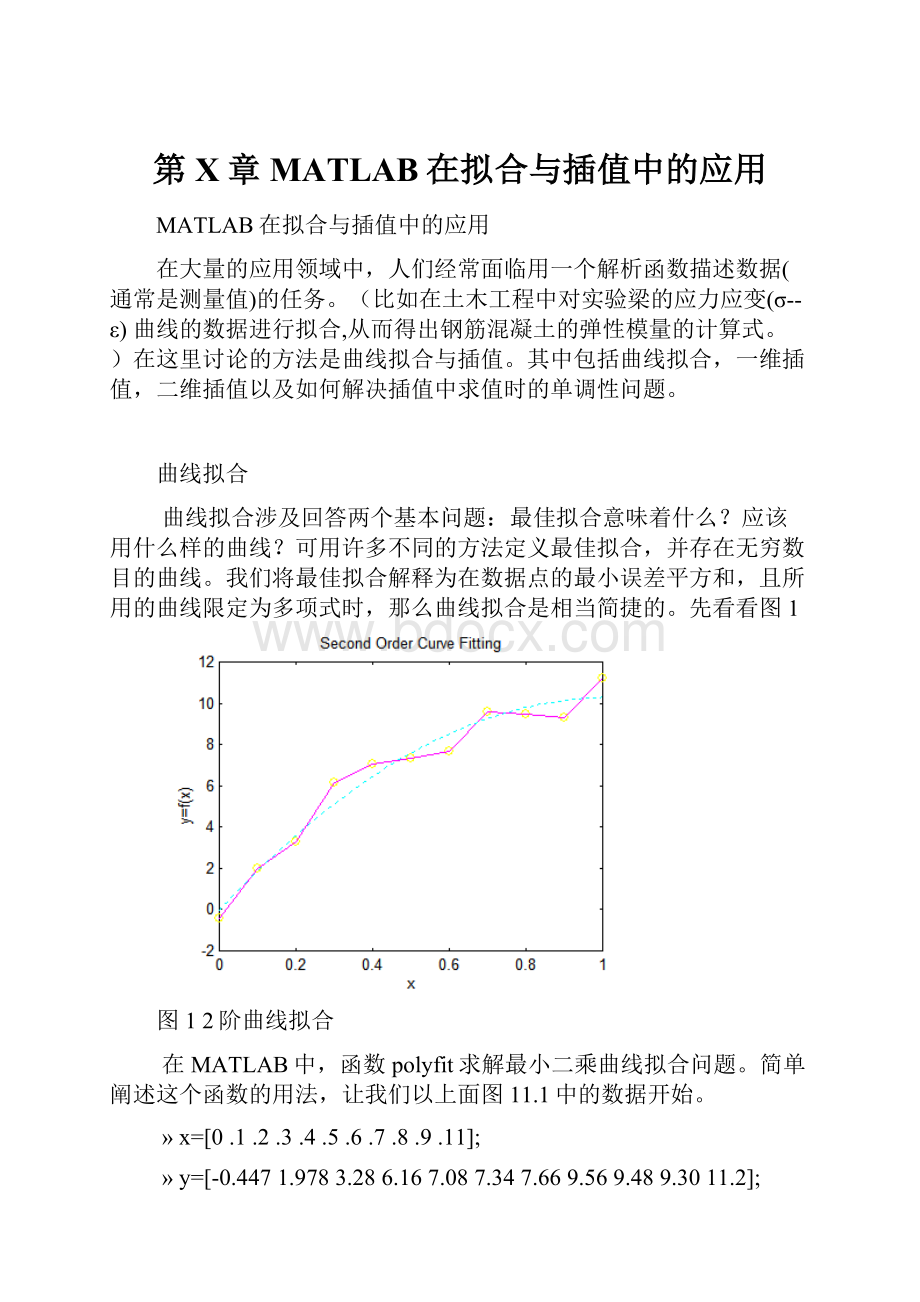
先看看图1
图12阶曲线拟合
在MATLAB中,函数polyfit求解最小二乘曲线拟合问题。
简单阐述这个函数的用法,让我们以上面图11.1中的数据开始。
»x=[0.1.2.3.4.5.6.7.8.9.11];
»y=[-0.4471.9783.286.167.087.347.669.569.489.3011.2];
为了用polyfit,我们必须给函数赋予上面的数据和我们希望最佳拟合数据的多项式的阶次或度。
如果我们选择n=1作为阶次,得到最简单的线性近似。
通常称为线性回归。
如果我们选择n=2作为阶次,得到一个2阶多项式。
»n=2;%polynomialorder
»p=polyfit(x,y,n)
p=
-9.810820.1293-0.0317
polyfit的输出是一个多项式系数的行向量。
其解是y=-9.8108x2+20.1293x-0.0317。
为了将曲线拟合解与数据点比较,把二者都绘成图。
»xi=linspace(0,1,100);%x-axisdataforplotting
»z=polyval(p,xi);
为了计算在xi数据点的多项式值,调用MATLAB的函数polyval。
»plot(x,y,'o',x,y,xi,z,':
')
画出了原始数据x和y,用'o'标出该数据点,在数据点之间,再用直线重画原始数据,并用点':
'线,画出多项式数据xi和z。
»xlabel('x'),ylabel('y=f(x)'),title('SecondOrderCurveFitting')
将图作标志。
这些步骤的结果表示于前面的图1中。
多项式阶次的选择是有点任意的。
两点决定一直线或一阶多项式。
三点决定一个平方或2阶多项式。
按此进行,n+1数据点唯一地确定n阶多项式。
于是,在上面的情况下,有11个数据点,我们可选一个高达10阶的多项式。
然而,高阶多项式给出很差的数值特性,我们不应选择比所需的阶次高的多项式。
此外,随着多项式阶次的提高,近似变得不够光滑,因为较高阶次多项式在变零前,可多次求导。
不妨选一个10阶多项式
»pp=polyfit(x,y,10);
»formatshorte
»pp.'
则ans=
-4.6436e+005
2.2965e+006
-4.8773e+006
5.8233e+006
-4.2948e+006
2.0211e+006
-6.0322e+005
1.0896e+005
-1.0626e+004
4.3599e+002
-4.4700e-001
要注意在现在情况下,多项式系数的规模与前面的2阶拟合的比较。
还要注意在最小(-4.4700e-001)和最大(5.8233e+006)系数之间有7个数量级的幅度差。
将这个解作图,并把此图与原始数据及2阶曲线拟合相比较。
»zz=polyval(pp,xi);
»plot(x,y,'o',xi,z,':
',xi,zz)
»xlabel('x'),ylabel('y=f(x)'),title('2ndand10thOrdercurveFitting')
在下面的图11.2中,原始数据标以'o',2阶曲线拟合是虚线,10阶拟合是实线。
注意,在10阶拟合中,在左边和右边的极值处,数据点之间出现大的纹波。
当企图进行高阶曲线拟合时,这种纹波现象经常发生。
根据图2,显然,‘越多就越好’在这里不适用。
图22阶和10阶曲线拟合
一维插值
正如曲线拟合所描述的那样,插值定义为对数据点之间函数的估值方法,这些数据点是由某些集合给定。
当我们不能很快地求出所需中间点的函数值时,插值是一个有价值的工具。
例如,当数据点是某些实验测量的结果或是过长的计算过程时,就有这种情况。
举例一维插值,考虑下列问题,(由于手头没有我们专业相关的实验数据,故采用老师经常提到的测温的例子,只是数据名称不一样)12小时内,一小时测量一次室外温度。
数据存储在两个MATLAB变量中。
»hours=1:
12;%indexforhourdatawasrecorded
»temps=[589152529313022252724];%recordedtemperatures
»plot(hours,temps,hours,temps,'+')%viewtemperatures
»title('Temperature')
»xlabel('Hour'),ylabel('DegreesCelsius')
图3在线性插值下室外温度曲线
正如图3看到的,MATLAB画出了数据点线性插值的直线。
为了计算在任意给定时间的温度,人们可试着对可视的图作解释。
另外一种方法,可用函数interp1。
»t=interp1(hours,temps,9.3)%estimatetemperatureathour=9.3
t=
22.9000
»t=interp1(hours,temps,4.7)%estimatetemperatureathour=4.7
t=
22
»t=interp1(hours,temps,[3.26.57.111.7])%findtempatmanypoints!
t=
10.2000
30.0000
30.9000
24.9000
若不采用直线连接数据点,我们可采用某些更光滑的曲线来拟合数据点。
最常用的方法是用一个3阶多项式,即3次多项式,来对相继数据点之间的各段建模,每个3次多项式的头两个导数与该数据点相一致。
这种类型的插值被称为3次样条或简称为样条。
函数interp1也能执行3次样条插值。
(这在工程中经常用到)
»t=interp1(hours,temps,9.3,'spline')%estimatetemperatureathour=9.3
t=
21.8577
»t=interp1(hours,temps,4.7,'spline')%estimatetemperatureathour=4.7
t=
22.3143
»t=interp1(hours,temps,[3.26.57.111.7],'spline')
t=
9.6734
30.0427
31.1755
25.3820
样条插值得到的结果,与上面所示的线性插值的结果不同。
因为插值是一个估计或猜测的过程,其意义在于,应用不同的估计规则导致不同的结果。
一个最常用的样条插值是对数据平滑。
也就是,给定一组数据,使用样条插值在更细的间隔求值。
例如,
»h=1:
0.1:
12;%estimatetemperatureevery1/10hour
»t=interp1(hours,temps,h,'spline');
»plot(hours,temps,'-',hours,temps,'+',h,t)%plotcomparativeresults
»title('SpringfieldTemperature')
»xlabel('Hour'),ylabel('DegreesCelsius')
在图4中,虚线是线性插值,实线是平滑的样条插值,标有'+'的是原始数据。
如要求在时间轴上有更细的分辨率,并使用样条插值,我们有一个更平滑、但不一定更精确地对温度的估计。
尤其应注意,在数据点,样条解的斜率不突然改变。
作为这个平滑插值的回报,3次样条插值要求更大量的计算,因为必须找到3次多项式以描述给定数据之间的特征。
图4在不同插值下室外温度曲线
二维插值
二维插值是基于与一维插值同样的基本思想。
然而,正如名字所隐含的,二维插值是对两变量的函数z=f(x,y)进行插值(比如钢筋混凝土实验中的正应力和剪应力都对挠度产生影响)。
这里依然考虑温度问题。
(数据由课件中改动而成)设人们对平板上的温度分布估计感兴趣,给定的温度值取自平板表面均匀分布的格栅。
采集了下列的数据:
»width=1:
5;%indexforwidthofplate(i.e.,thex-dimension)
»depth=1:
3;%indexfordepthofplate(i,e,,they-dimension)
»temps=[8281808284;7963616581;8484828586]%temperaturedata
temps=
8281808284
7963616581
8484828586
如同在标引点上测量一样,矩阵temps表示整个平板的温度分布。
temps的列与下标depth或y-维相联系,行与下标width或x-维相联系(见图5)。
为了估计在中间点的温度,我们必须对它们进行辨识。
»wi=1:
0.2:
5;%estimateacrosswidthofplate
»d=2;%atadepthof2
»zlinear=interp2(width,depth,temps,wi,d);%linearinterpolation
»zcubic=interp2(width,depth,temps,wi,d,'cubic');%cubicinterpolation
»plot(wi,zlinear,'-',wi,zcubic)%plotresults
»xlabel('WidthofPlate'),ylabel('DegreesCelsius')
»title(['TemperatureatDepth='num2str(d)])
另一种方法,我们可以在两个方向插值。
先在三维坐标画出原始数据,看一下该数据的粗糙程度(见图6)。
»mesh(width,depth,temps)%usemeshplot
»xlabel('WidthofPlate'),ylabel('DepthofPlate')
»zlabel('DegreesCelsius'),axis('ij'),grid
图5在深度d=2处的平板温度
图6平板温度
然后在两个方向上插值,以平滑数据。
»di=1:
0.2:
3;%choosehigherresolutionfordepth
»wi=1:
0.2:
5;%choosehigherresolutionforwidth
»zcubic=interp2(width,depth,temps,wi,di,'cubic');%cubic
»mesh(wi,di,zcubic)
»xlabel('WidthofPlate'),ylabel('DepthofPlate')
»zlabel('DegreesCelsius'),axis('ij'),grid
该例子清楚地证明了,二维插值更为复杂,只是因为有更多的量要保持跟踪。
interp2的基本形式是interp2(x,y,z,xi,yi,method)。
这里x和y是两个独立变量,z是一个应变量矩阵。
x和y对z的关系是
z(i,:
)=f(x,y(i))和z(:
j)=f(x(j),y).
也就是,当x变化时,z的第i行与y的第i个元素y(i)相关,当y变化时,z的第j列与x的第j个元素x(j)相关,。
xi是沿x-轴插值的一个数值数组;yi是沿y-轴插值的一个数值数组。
图7二维插值后的平板温度
虽然对于许多应用,函数interp1和interp2是很有用的,但它们限制为对单调向量进行插值。
在某些情况,这个限制太严格。
例如,考虑下面的插值:
»x=linspace(0,5);
»y=1-exp(-x).*sin(2*pi*x);
»plot(x,y)
图8函数1-exp(-x).*sin(2*pi*x)的曲线
函数interp1可用来在任何值或x的值上估计y值。
»yi=interp1(x,y,1.8)
yi=
1.1556
然而,interp1不能找出对应于某些y值的x值。
例如,如在图8上所示,考虑寻找y=1.1处的x值:
图8给y值在函数曲线上求x的值
»plot(x,y,[0,5],[1.11.1])
从图8上,我们看到有四个交点。
使用interp1,我们得到:
»xi=interp1(y,x,1.1)
?
?
?
Errorusing==>table1
Firstcolumnofthetablemustbemonotonic.
这个函数interp1失败,由于y不是单调的。
如何消除了单调性的要求(我尝试搜索了一些资料,对此问题可由如下解答)
»table=[x;y].';%createcolumnorientedtablefromdata
»xi=mminterp(table,2,1.1)
xi=
0.52811.1000
0.95801.1000
1.58251.1000
1.88471.1000
这里使用了线性插值,函数mminterp估计了y=1.1处的四个点。
由于函数mminterp的一般性质,要插值的数据是由面向列矩阵给出,在上面的例子中称作为表(table)。
第二个输入参量是被搜索矩阵table的列,第三个参量是要找的值。
函数的主体由下面给出:
functiony=mminterp(tab,col,val)
%MMINTERP1-DTableSearchbyLinearInterpolation.
%Y=MMINTERP(TAB,COL,VAL)linearlyinterpolatesthetable
%TABsearchingforthescalarvalueVALinthecolumnCOL.
%AllcrossingsarefoundandTAB(:
COL)neednotbemonotonic.
%EachcrossingisreturnedasaseparaterowinYandYhasas
%manycolumnsasTAB.Naturally,thecolumnCOLofYcontains
%thevalueVAL.IfVALisnotfoundinthetable,Y=[].
[rt,ct]=size(tab);
iflength(val)>1,error('VALmustbeascalar.'),end
ifcol>ct|col<1,error('Chosencolumnoutsidetablewidth.'),end
ifrt<2,error('Tabletoosmallornotorientedincolumns.'),end
above=tab(:
col)>val;%Truewhere>VAL
below=tab(:
col)equal=tab(:
col)==val;%Truewhere=VAL
ifall(above==0)|all(below==0),%handlesimplestcase
y=tab(find(equal),:
);return
end
pslope=find(below(1:
rt-1)&above(2:
rt));%indiceswhereslopeis+
nslope=find(below(2:
rt)&above(1:
rt-1));%indiceswhereslopeis-
ib=sort([pslope;nslope+1]);%putindicesbelowinorder
ia=sort([nslope;pslope+1]);%putindicesaboveinorder
ie=find(equal);%indiceswhereequaltoval
[tmp,ix]=sort([ib,ie]);%findwhereequalsfitinresult
ieq=ix>length(ib);%Truewhereequalsvaluesfit
ry=length(tmp);%#ofrowsinresulty
y=zeros(ry,ct);%pokedataintoazeromatrix
alpha=(val-tab(ib,col))./(tab(ia,col)-tab(ib,col));
alpha=alpha(:
ones(1,ct));%duplicateforallcolumns
y(~ieq,:
)=alpha.*tab(ia,:
)+(1-alpha).*tab(ib,:
);%interpolatedvalues
y(ieq,:
)=tab(ie,:
);%equalvalues
y(:
col)=val*ones(ry,1);%removeroundofferror
正如所见的,mminterp利用了find和sort函数、逻辑数组和数组操作技术。
没有For循环和While循环。
不论用其中哪一种技术来实现将使运行变慢,尤其对大的表。
mminterp与含有大于或等于2的任意数列的表一起工作,如同函数interp1一样。
而且,在这种情况下,插值变量可以是任意的列。
例如,
»z=sin(pi*x);%addmoredatatotable
»table=[x;y;z].';
»t=mminterp(table,2,1.1)%sameinterpolationasearlier
t=
0.52811.10000.9930
0.95801.10000.1314
1.58251.1000-0.9639
1.88471.1000-0.3533
»t=mminterp(table,3,-.5)%secondthirdcolumnnow
t=
1.16690.7316-0.5000
1.83291.1377-0.5000
3.16710.9639-0.5000
3.83311.0187-0.5000
这些最后的结果估计了x和y在z=-0.5处的值。
小结
曲线的插值和拟合是一个很复杂的工作,但在MATLAB中能由几句轻松的命令来实现,为工程技术人员和科研工作者带来极大的方便,让人不禁感叹它的强大,实为工科学生必备之工具!
!
下面的表总结了在MATLAB中所具有的曲线拟合和插值函数。
可供同学们参考。
。
。
曲线拟合和插值函数
polyfit(x,y,n)
对描述n阶多项式y=f(x)的数据
进行最小二乘曲线拟合
interp1(x,y,xo)
1维线性插值
interp1(x,y,xo,'spline')
1维3次样条插值
interp1(x,y,xo,'cubic')
1维3次插值
interp2(x,y,Z,xi,yi)
2维线性插值
interp2(x,y,Z,xi,yi,'cubic')
2维3次插值
interp2(x,y,Z,xi,yi,'nearest')
2维最近邻插值
参考文献《精通Matlab综合辅导与指南》