最小二乘估计及模型阶次辨【范本模板】.doc
《最小二乘估计及模型阶次辨【范本模板】.doc》由会员分享,可在线阅读,更多相关《最小二乘估计及模型阶次辨【范本模板】.doc(9页珍藏版)》请在冰豆网上搜索。
实验二最小二乘估计及模型阶次辨识
一、实验目的
①通过实验,掌握最小二乘参数辨识方法
②通过实验,掌握模型阶次辨识方法
二、实验内容
1、仿真模型
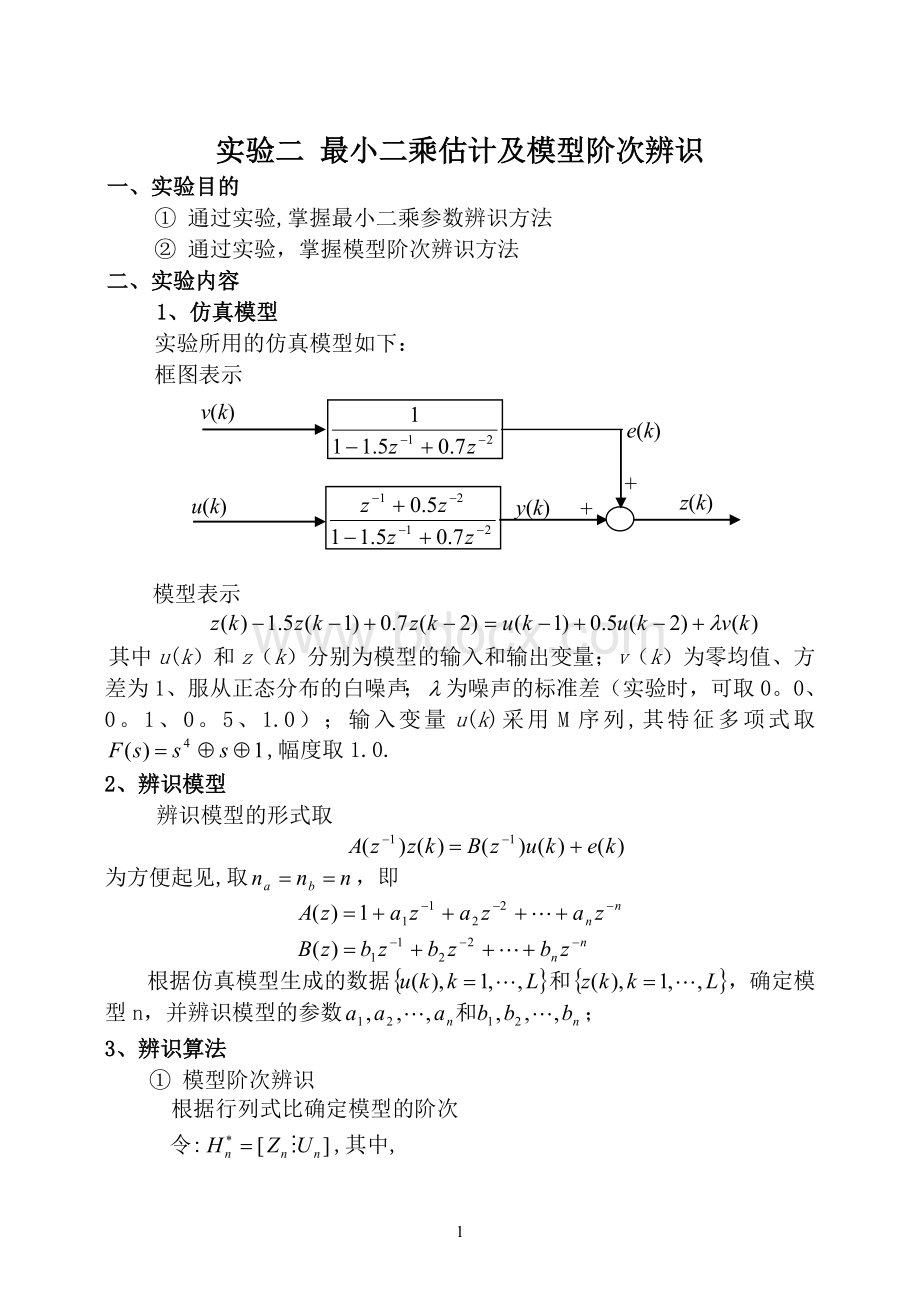
实验所用的仿真模型如下:
框图表示
e(k)
+
+
v(k)
u(k)
z(k)
y(k)
模型表示
其中u(k)和z(k)分别为模型的输入和输出变量;v(k)为零均值、方差为1、服从正态分布的白噪声;为噪声的标准差(实验时,可取0。
0、0。
1、0。
5、1.0);输入变量u(k)采用M序列,其特征多项式取,幅度取1.0.
2、辨识模型
辨识模型的形式取
为方便起见,取,即
根据仿真模型生成的数据和,确定模型n,并辨识模型的参数;
3、辨识算法
①模型阶次辨识
根据行列式比确定模型的阶次
令:
其中,
定义判别式子(行列式比):
其中:
若较有显著增加时,则取阶次估计值为.
②模型参数辨识:
最小二乘一次完成算法:
设输入信号的取值是从k=1到k=16的M序列,则待辨识参数为=.其中,被辨识参数、观测矩阵zL、HL的表达式为
,
三、实验步骤
(1)掌握最小二乘一次完成算法和根据行列式比确定模型的阶次的基本原理。
(2)设计实验方案。
(3)编制实验程序.
(4)调试程序,研究实验问题,记录数据。
(5)分析实验结果,完成实验报告。
四、实验结果
(1)实验对象及参数
实验模型如下图所示:
(2)程序代码:
a.主函数
functionleastSquaresMainFuc
a1=1.5;a2=-0。
7;b1=1;b2=0。
5;
DR=estModelOrder(a1,a2,b1,b2);
display(DR);
estimate=leastSquares(a1,a2,b1,b2);
display(estimate);
recursiveLeastSquares(a1,a2,b1,b2)
end
b。
模型阶次辨识函数
functionDR=estModelOrder(a1,a2,b1,b2)
x=[010110111];%initialvalue
n=1003;%n为脉冲数目,L=1000,且存在k-2,故取1003
M=[];%存放M序列
fori=1:
n
temp=xor(x(4),x(9));
M(i)=x(9);
forj=9:
-1:
2
x(j)=x(j—1);
end
x
(1)=temp;
end
%产生高斯白噪声
v=randn(1,1003);
z=[];
z
(1)=-1;
z
(2)=0;
L=1000;
fori=3:
L+3
z(i)=a1*z(i—1)+a2*z(i—2)+b1*M(i—1)+b2*M(i-2)+v(i);
end
%n=1
fori=1:
L
H1(i,1)=z(i);
H1(i,2)=M(i);
end
A=H1’*H1/L;
%n=2
fori=1:
L
H2(i,1)=z(i+1);
H2(i,2)=z(i);
H2(i,3)=M(i+1);
H2(i,4)=M(i);
end
B=H2'*H2/L;
%n=3
fori=1:
L
H3(i,1)=z(i+2);
H3(i,2)=z(i+1);
H3(i,3)=z(i);
H3(i,4)=M(i+2);
H3(i,5)=M(i+1);
H3(i,6)=M(i);
end
C=H3’*H3/L;
%n=4
fori=1:
L
H4(i,1)=z(i+3);
H4(i,2)=z(i+2);
H4(i,3)=z(i+1);
H4(i,4)=z(i);
H4(i,5)=M(i+3);
H4(i,6)=M(i+2);
H4(i,7)=M(i+1);
H4(i,8)=M(i);
end
D=H4'*H4/L;
DR
(1)=det(A)/det(B);
DR
(2)=det(B)/det(C);
DR(3)=det(C)/det(D);
i=1:
3;
figure
(1)
stem(i,DR);
%display(DR)
title(’利用行列式比估计模型阶次’)
xlabel('阶次’)
ylabel('行列式比’)
end
c。
批量最小二乘估计
functionestimate=leastSquares(a1,a2,b1,b2)
x=[010110111];%initialvalue
n=403;%n为脉冲数目
M=[];%存放M序列
fori=1:
n
temp=xor(x(4),x(9));
M(i)=x(9);
forj=9:
-1:
2
x(j)=x(j-1);
end
x
(1)=temp;
end
%产生均值为0,方差为1的高斯白噪声
v=randn(1,400);
z=[];
z
(1)=-1;
z
(2)=0;
fori=3:
402
z(i)=a1*z(i—1)+a2*z(i-2)+b1*M(i—1)+b2*M(i—2)+v(i—2);
end
H=zeros(400,4);
fori=1:
400
H(i,1)=—z(i+1);
H(i,2)=-z(i);
H(i,3)=M(i+1);
end
H(i,4)=M(i);
estimate=inv(H'*H)*H’*(z(3:
402))';
end
d。
最小二乘的递推算法的参数估计
functionrecursiveLeastSquares(a1,a2,b1,b2)
x=[010110111];%initialvalue
n=403;%n为脉冲数目
M=[];%存放M序列
fori=1:
n
temp=xor(x(4),x(9));
M(i)=x(9);
forj=9:
—1:
2
x(j)=x(j—1);
end
x
(1)=temp;
end
%===========产生均值为0,方差为1的高斯白噪声=========
v=randn(1,400);
%==============产生观测序列z=================
z=zeros(402,1);
z
(1)=—1;
z
(2)=0;
fori=3:
402
z(i)=a1*z(i—1)+a2*z(i—2)+b1*M(i-1)+b2*M(i—2)+v(i-2);
end
%递推求解
P=100*eye(4);%估计方差
Pstore=zeros(4,401);
Pstore(:
,1)=[P(1,1),P(2,2),P(3,3),P(4,4)];
Theta=zeros(4,401);%参数的估计值,存放中间过程估值
Theta(:
,1)=[3;3;3;3];
%K=zeros(4,400);%增益矩阵
K=[10;10;10;10];
fori=3:
402
h=[-z(i-1);-z(i—2);M(i-1);M(i—2)];
K=P*h*inv(h'*P*h+1);
Theta(:
,i—1)=Theta(:
,i—2)+K*(z(i)-h’*Theta(:
i—2));
P=(eye(4)—K*h’)*P;
Pstore(:
,i-1)=[P(1,1),P(2,2),P(3,3),P(4,4)];
end
i=1:
401;
figure
(2);
plot(i,Theta(1,:
),i,Theta(2,:
),i,Theta(3,:
),i,Theta(4,:
))
title('待估参数过渡过程');
figure(3);
plot(i,Pstore(1,:
),i,Pstore(2,:
),i,Pstore(3,:
),i,Pstore(4,:
))
title('估计方差变化过程’);
end
(3)实验结果及其分析
1)行列式比法模型阶次估计图形如下
2)递推最小二乘估计
参数过渡过程如下图所示:
由上图可知,方差逐渐较小,并且趋近去0,说明估计递推过程基本完成。
(4)心得体会
通过本次试验,我不仅学到了噪声生成和系统辨识的方法,也复习了Matlab编程的方法。
在这次试验中,无论是专业课知识还是动手能力上都得到了更高层次提升。
9