小学及小升初复习阴影部分求面积及周长用含完整答案2.docx
《小学及小升初复习阴影部分求面积及周长用含完整答案2.docx》由会员分享,可在线阅读,更多相关《小学及小升初复习阴影部分求面积及周长用含完整答案2.docx(16页珍藏版)》请在冰豆网上搜索。
小学及小升初复习阴影部分求面积及周长用含完整答案2
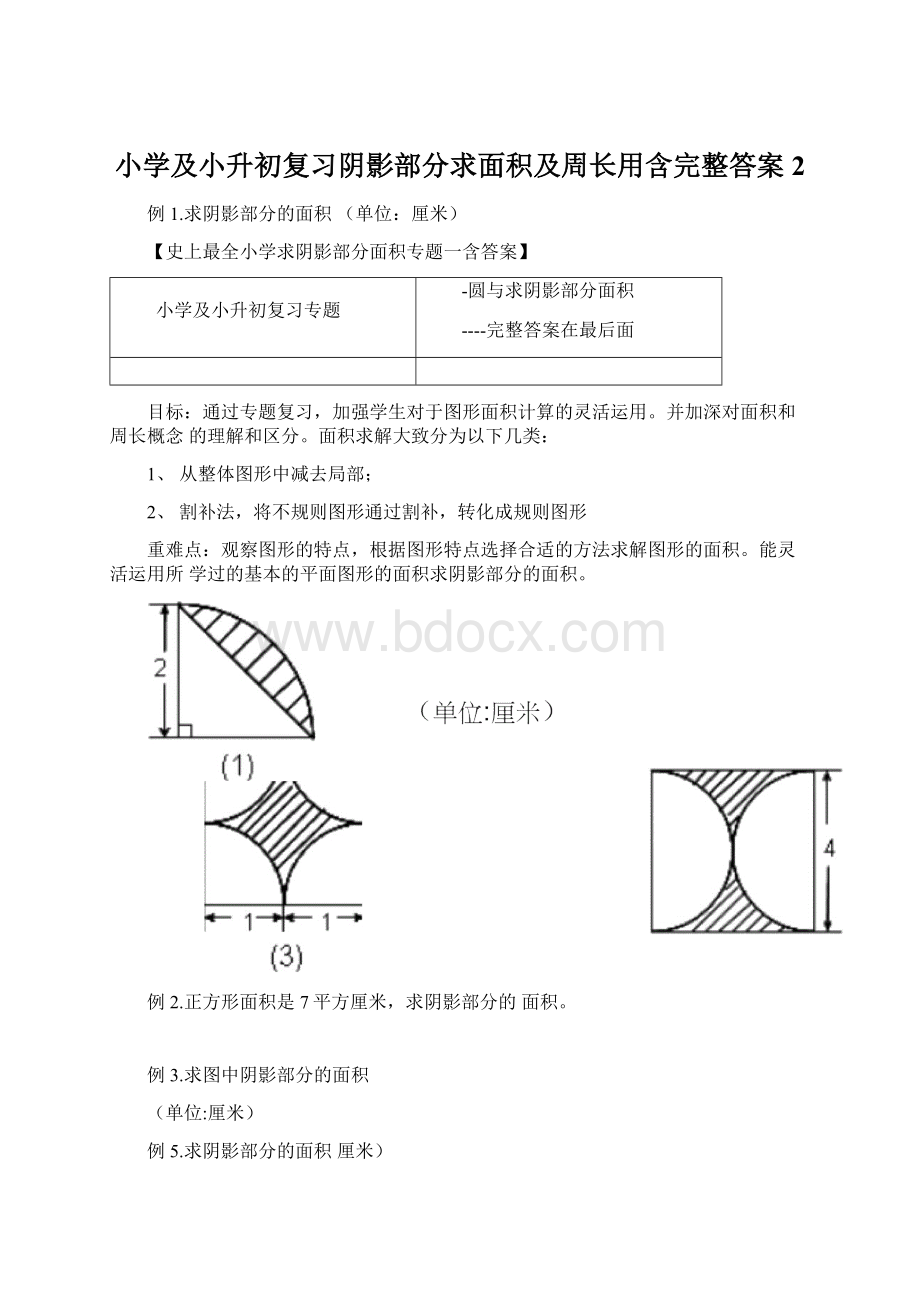
例1.求阴影部分的面积(单位:
厘米)
【史上最全小学求阴影部分面积专题一含答案】
小学及小升初复习专题
-圆与求阴影部分面积
----完整答案在最后面
目标:
通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:
1、从整体图形中减去局部;
2、割补法,将不规则图形通过割补,转化成规则图形
重难点:
观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例2.正方形面积是7平方厘米,求阴影部分的面积。
例3.求图中阴影部分的面积
(单位:
厘米)
例5.求阴影部分的面积厘米)
⑵
例4.求阴影部分的面积。
(单位:
厘米)
例6.如图:
已知小圆半径为2厘米,大圆半径
是小圆的3倍,问:
空白部分甲比乙的面积多
多少厘米?
(6)
例7.求阴影部分的面积。
厘米)
(单位:
例9.求阴影部分的面积。
(单位:
厘米)
例11.求阴影部分的面积。
仲位:
厘米)
(11)
例13.求阴影部分的面积。
(单位:
厘米)
(13)
例8.求阴影部分的面积。
(单位:
厘米)
例10.求阴影部分的面积。
(单位:
厘米)
例12.求阴影部分的面积。
(单位:
厘米)
(10)
(12)
例14.求阴影部分的面积。
(单位:
厘米)
(14)
例15.已知直角三角形面积是阴影部分的面积。
12平方厘米,求
例16.求阴影部分的面积。
(单位:
厘米)
(15)
(16)
例17•图中圆的半径为5厘米,求阴影部分的面积。
(单位:
厘米)
例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
A
E
(V)
(18)
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积
D
C
———401
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正万形边长为8厘米,求阴影部分的面积。
(22)
(23)
0)
A
(25)
B
D
B
128)
(27)
B
0
(30)
(29)
A
C
E
(34)
B
(32)
5°
角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,/CBD=「「,问:
阴影部分...
甲比乙面积小多少?
K亠
例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
例33.求阴影部分的面积。
仲位:
厘米)
例34.求阴影部分的面积。
(单位:
厘米)
例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
部分甲比阴影部分乙面积大28平方厘米AB=40厘米。
求BC的长度。
10—
J2
S8
(31)
【专1】下图中,大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积
【专1-1】.右图中,大小正方形的边长分别是12厘米和10厘米。
求阴影部分面积
【专1-2】.求右图中阴影部分图形的面积及周长
&厘米»
【专2】已知右图阴影部分三角形的面积是5平方米,求圆的面积。
【专2-1】已知右图中,圆的直径是2厘米,求阴影部分的面积
【专2-3】求下图中阴影部分的面积。
(单位:
厘米)
64
【专3】求下图中阴影部分的面
【专3-1】求右图中阴影部分的
【专3-2】求右图中阴影部分的面积
4J
【专3-3】求下图中阴影部分的面积
奄5歴米►
完整答案
1
例1解:
这是最基本的方法:
4圆面积减去等腰直角三角形的面积,
TI
石爼込2X1=1.14(平方厘米)
例2解:
这也是一种最基本的方法用正方形的
1
面积减去W圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以r2=7,
所以阴影部分的面积为:
7-4严=7-4
X7=1.505平方厘米
1
例4解:
同上,正方形面积减去圆面积,
例3解:
最基本的方法之一。
用四个d圆组成
16-n()=16-4n
一个圆,用正方形的面积减去圆的面积,
=3.44平方厘米
所以阴影部分的面积:
2X2-n=0.86平方
厘米。
例5解:
这是一个用最常用的方法解最常见的
例6解:
两个空白部分面积之差就是两圆面积
题,为方便起见,
之差(全加上阴影部分)
我们把阴影部分的每一个小部分称为叶
n2-n()=100.48平方厘米
形”是用两个圆减去一个正方形,
(注:
这和两个圆是否相交、交的情况如
n()X-16=8n-16=9.12平方厘米
另外:
此题还可以看成是1题中阴影部分
何无关)
的8倍。
例7解:
正方形面积可用(对角线长X寸角线长
例8解:
右面正方形上部阴影部分的面积,等
吃,求)
于左面正方形下部空白部分面积,割补以后为
正方形面积为:
5X5吃=12.5
1
(5)2
玄圆,
所以阴影面积为:
n*12.5=7.125
1
平方厘米
所以阴影部分面积为:
4n()=3.14平方
(注:
以上几个题都可以直接用图形的差来
厘米
求,无需割、补、增、减变形)
例9解:
把右面的正方形平移至左边的正方形
例10解:
同上,平移左右两部分至中间部分,
部分,则阴影部分合成一个长方形,
则合成一个长方形,
所以阴影部分面积为:
2X3=6平方厘米
所以阴影部分面积为2X1=2平方厘米(注:
8、9、10三题是简单割、补或平移)
例11解:
这种图形称为环形,可以用两个同
例12.解:
三个部分拼成一个半圆面积.
心圆的面积差或差的一部分来求。
2
r607
n()迪=14.13平方厘米
(冗4”-n")X光。
=6>3.14=3.66平方厘
米
例13解:
连对角线后将"叶形"剪开移到右上面
1
的空白部分,凑成正方形的一半.
例14解:
梯形面积减去4圆面积,
所以阴影部分面积为:
8X8吃=32平方厘
1丄2
米
2(4+10)X4-4n=28-4n=15.44平方厘
米.
例15.分析:
此题比上面的题有一定难度,这是"叶形"的一个半.
1r0
例16解:
了[+詁-少“]
1
解:
设三角形的直角边长为r,则云2=12,了
1
=1n(11&36)=40n=125.6平方厘米
=6
圆面积为:
冗2宁2=3n圆内三角形的面
积为12^2=6,
J
阴影部分面积为:
(3n-6)刃=5.13平方厘
米
例17解:
上面的阴影部分以AB为轴翻转后,
例18解:
阴影部分的周长为三个扇形弧,拼
整个阴影部分成为梯形减去直角三角形,或两
在一起为一个半圆弧,
个小直角三角形AED、BCD面积和。
所以圆弧周长为:
2X3.14X3十2=9.42厘米
所以阴影部分面积为:
5X5吃+5X10吃=37.5平方厘米
例19解:
右半部分上面部分逆时针,下面部
例20解:
设小圆半径为r,4F=36,r=3,大圆
分顺时针旋转到左半部分,组成一个矩形。
口2
所以面积为:
1X2=2平方厘米
半径为R,尺=2”=18,
将阴影部分通过转动移在一起构成半个
圆环,
所以面积为:
n(-F)-2=4.5n=14.13f
方厘米
例21.解:
把中间部分分成四等分,分别放在
例22解法一:
将左边上面一块移至右边上面,
上面圆的四个角上,补成一个正方形,边长为
补上空白,则左边为一三角形,右边一个半圆.
2厘米,
阴影部分为一个三角形和一个半圆
所以面积为:
2X2=4平方厘米
面积之和.
)-2+4X4=8n+16=41.1平
方厘米
解法二:
补上两个空白为一个完
整的圆.
(22)
1
所以阴影部分面积为一个圆减去一
个叶形,叶形面积为:
冗气)-2-4X4=8n-16
所以阴影部分的面积
为:
n()-8n+16=41.12平方厘米
例23解:
面积为4个圆减去8个叶形,叶形
11
例24分析:
连接角上四个小圆的圆心构成一
—仃—
面积为:
f-1X=2n-1
3
.1
个正方形,各个小圆被切去环个圆,
所以阴影部分的面积为:
4-8(2
这四个部分正好合成3个整圆,而正方形中的
n-1)=8平方厘米
空白部分合成两个小圆.
解:
阴影部分为大正方形面积与一个小圆面积之和.
为:
4X4+n=19.1416平方厘米
例25分析:
四个空白部分可以拼成一个以2
例26解:
将三角形CEB以B为圆心,逆时针
为半径的圆.
转动90度,到三角形ABD位置,阴影部分成
所以阴影部分的面积为梯形面积减去
1
圆的面积,
为三角形ACB面积减去4个小圆面积,
4X(4+7)-2-冗严=22-4n=9.44平方厘米
为:
5X吃-n2^4=12.25-3.14=9.36平方
厘米
例27解:
因为2=心=4,所以
例28解法一:
设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,
心=2
三角形ABD的面积为:
5X吃=12.5
以AC为直径的圆面积减去三角形ABC
2
弓形面积为:
[吃-5X5]-2=7.125
面积加上弓形AC面积,
所以阴影面积为:
12.5+7.125=19.625平
亍』尸-2X2-4+[严尸-4-2]
11
方厘米
解法二:
右上面空白部分为小正方形面积减去
=2n-1+(丄n-1)
=n-2=1.14平方厘米
1125
凹小圆面积,其值为:
5X5-却n"=25-n
阴影面积为三角形ADC减去空白部分面
2525
积,为:
10X5P-(25-4n)=厲冗=19.625
平方厘米
例29.解:
甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形
ABC,
竺1
例30.解:
两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则
2(12
40X-2-吃=28
所以40X-400n=56贝UX=32.8厘米
此两部分差即为:
n^x3和-7x1x6=
5n-12=3.7平方厘米
例31.解:
连PD、PC转换为两个三角形和
1
两个弓形,
例32解:
三角形DCE的面积为:
/X4X10=20
两三角形面积为:
△APD面积+△QPC面
1
平方厘米
1
积=亍(5X10+5X5)=37.5
梯形ABCD的面积为7(4+6)>4=20平方
-(5)2
两弓形PC、PD面积为:
2冗-5X
厘米从而知道它们面积相等,则三角形ADF
1
面积等于三角形EBF面积,阴影部分可补成4
圆ABE的面积,其面积为:
25
所以阴影部分的面积为:
37.5+3
n-25=51.75平方厘米
n2-4=9n=28.26^方厘米
1
例33.解:
用N大圆的面积减去长方形面积再加
例34解:
两个弓形面积为:
[戸-3>4吃=4
1
上一个以2为半径的4圆ABE面积,为
n-6
阴影部分为两个半圆面积减去两个弓形
1屮
面积,结果为
4(n+n2-)-6
1
=~aX13t-6
(呼25925
n,+n'-(4n-6)=n(4+^-4)
=4.205平方厘米
+6=6平方厘米
1
例35解:
将两个同样的图形拼在一起成为T圆
减等腰直角三角形
1
(5)27
[n"詔-」X5X5]-2
2525
=(耳n-2)吃=3.5625平方厘米
举一反三★巩固练习-answer
【专1】(5+9)X5-2+9X9-2—(5+9)X5-2=40.5(平方厘米)
【专1-1】(10+12)X10十2+3.14X12X12-4—(10+12)X10十2=113.04(平方厘米)
【专1-2】面积:
6X(6-2)—3.14X(6-2)X(6-2)十2=3.87(平方厘米)
周长:
3.14X6-2+6+(6-2)X2=21.42(厘米)
【专2]2rXr十2=5即rXr=5
圆的面积-一=3.14X5=15.7(平方厘米)
【专2-1]3.14X(2-2)X(2-2)—2X2-2=1.14(平方厘米)
【专2-2]面积:
3.14X6X6-4—3.14X(6-2)X(6-2)十2=14.13(平方厘米)周长:
2X3.14X6-4+3.14X6-2+6=24.84(厘米)
【专2-3](6+4)X4-2—(4X4—3.14X4X4-4)=16.56(平方厘米)
【专3]6X3—3X3-2=13.5(平方厘米)
【专3-1]8X(8-2)十2=16(平方厘米)
【专3-2]3.14X4X4-4—4X4-2=4.56(平方厘米)
【专3-3]5X5-2=12.5(平方厘米)