排列组合知识点与方法归纳.docx

排列组合知识点与方法归纳.docx

《排列组合知识点与方法归纳.docx》由会员分享，可在线阅读，更多相关《排列组合知识点与方法归纳.docx（14页珍藏版）》请在冰豆网上搜索。

排列组合知识点与方法归纳

排列组合知识点与方法归纳

排列组合

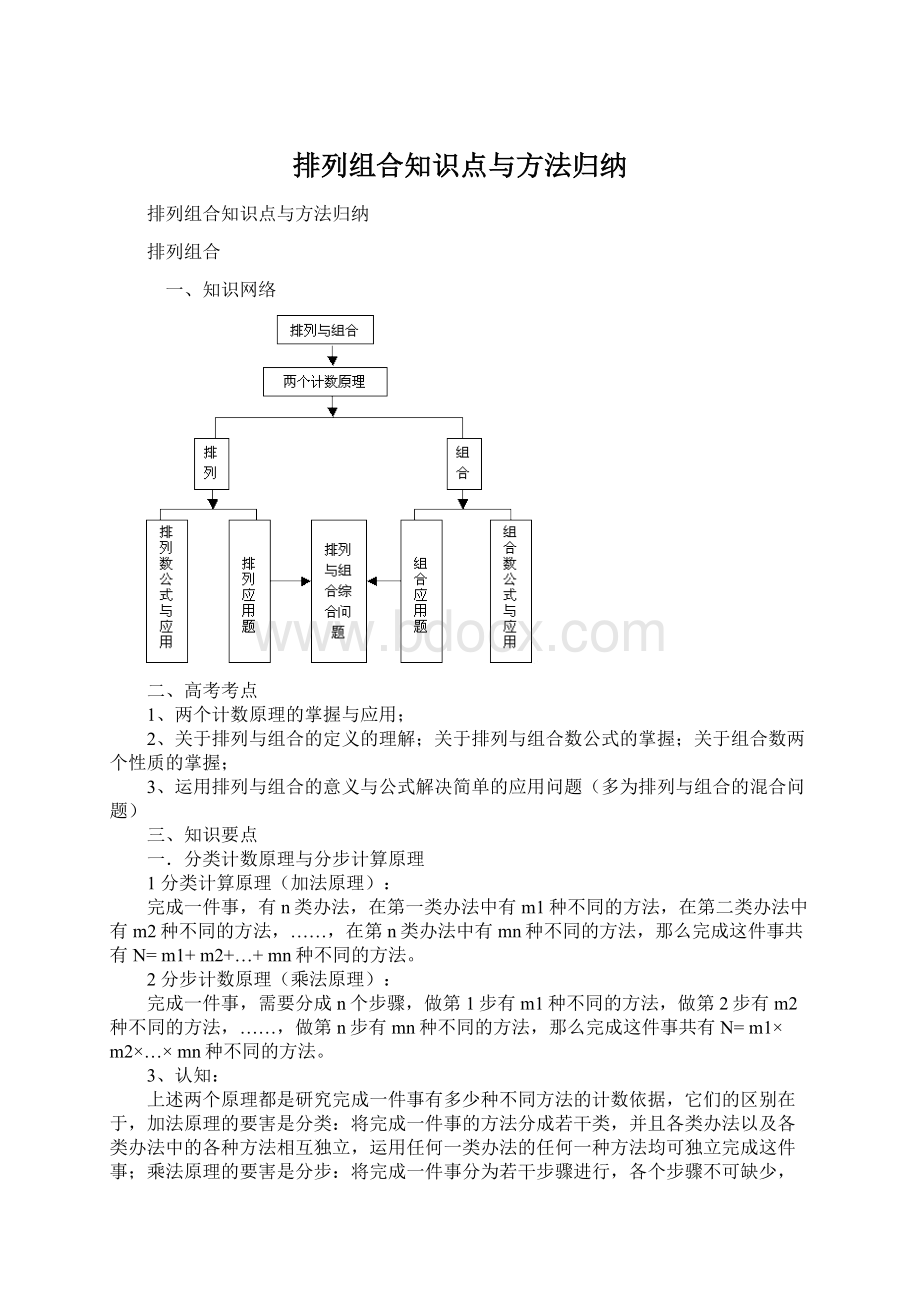
　一、知识网络

二、高考考点

　　1、两个计数原理的掌握与应用；

　　2、关于排列与组合的定义的理解；关于排列与组合数公式的掌握；关于组合数两个性质的掌握；

　　3、运用排列与组合的意义与公式解决简单的应用问题（多为排列与组合的混合问题）

　　三、知识要点

　　一．分类计数原理与分步计算原理

　　1分类计算原理（加法原理）：

　　完成一件事，有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+…+mn种不同的方法。

　　2分步计数原理（乘法原理）：

　　完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×…×mn种不同的方法。

　　3、认知：

　　上述两个原理都是研究完成一件事有多少种不同方法的计数依据，它们的区别在于，加法原理的要害是分类：

将完成一件事的方法分成若干类，并且各类办法以及各类办法中的各种方法相互独立，运用任何一类办法的任何一种方法均可独立完成这件事；乘法原理的要害是分步：

将完成一件事分为若干步骤进行，各个步骤不可缺少，只有当各个步骤依次完成后这件事才告完成（在这里，完成某一步的任何一种方法只能完成这一个步骤，而不能独立完成这件事）。

　　二．排列

　　1定义

（1）从n个不同元素中取出m（）个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一排列。

（2）从n个不同元素中取出m（）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，记为.

　　2排列数的公式与性质

（1）排列数的公式：

=n（n-1）（n-2）…（n-m+1）=　　特例：

当m=n时，=n！

=n（n-1）（n-2）…×3×2×1

　　规定：

0！

=1

（2）排列数的性质：

　　（Ⅰ）=（排列数上标、下标同时减1（或加1）后与原排列数的联系）

　　（Ⅱ）（排列数上标加1或下标减1后与原排列数的联系）

　　（Ⅲ）（分解或合并的依据）

　　三．组合

　　1定义　

（1）从n个不同元素中取出个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合

（2）从n个不同元素中取出个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号表示。

　　2组合数的公式与性质

（1）组合数公式：

（乘积表示）　（阶乘表示）　　特例：

（2）组合数的主要性质：

　　（Ⅰ）　　（上标变换公式）

　　（Ⅱ）　　（杨辉恒等式）

　　认知：

上述恒等式左边两组合数的下标相同，而上标为相邻自然数；合二为一后的右边组合数下标等于左边组合数下标加1，而上标取左边两组合数上标的较大者。

　　3比较与鉴别

　　由排列与组合的定义知，获得一个排列需要“取出元素”和“对取出元素按一定顺序排成一列”两个过程，而获得一个组合只需要“取出元素”，不管怎样的顺序并成一组这一个步骤。

（1）排列与组合的区别在于组合仅与选取的元素有关，而排列不仅与选取的元素有关，而且还与取出元素的顺序有关。

因此，所给问题是否与取出元素的顺序有关，是判断这一问题是排列问题还是组合问题的理论依据。

（2）注意到获得（一个）排列历经“获得（一个）组合”和“对取出元素作全排列”两个步骤，故得排列数与组合数之间的关系：

　　四、经典例题

　　例1、某人计划使用不超过500元的资金购买单价分别为60、70元的单片软件和盒装磁盘，要求软件至少买3片，磁盘至少买2盒，则不同的选购方式是（　　　　）

　　A.5种　　　　　　B.6种　　　　　　C.7种　　　　D.8种

　　分析：

依题意“软件至少买3片，磁盘至少买2盒”，而购得3片软件和2盒磁盘花去320元，所以，只需讨论剩下的180元如何使用的问题。

　　解：

注意到购买3片软件和2盒磁盘花去320元，所以，这里只讨论剩下的180元如何使用，可从购买软件的情形入手分类讨论：

　第一类，再买3片软件，不买磁盘，只有1种方法；　　第二类，再买2片软件，不买磁盘，只有1种方法；

第三类，再买1片软件，再买1盒磁盘或不买磁盘，有2种方法；第四类，不买软件，再买2盒磁盘、1盒磁盘或不买磁盘，有3种方法；　　于是由分类计数原理可知，共有N=1+1+2+3=7种不同购买方法，应选C。

　　例2、已知集合M={-1，0，1}，N={2，3，4，5}，映射，当x∈M时，为奇数，则这样的映射的个数是（　　）　　A.20　　　　B.18　　　　C.32　　　　D.24

　　分析：

由映射定义知，当x∈M时，

　　当x∈M时，这里的x可以是奇数也可以是偶数，但必须为奇数，因此，对M中x的对应情况逐一分析，分步考察：

　　第一步，考察x=-1的象，当x=-1时，，此时可取N中任一数值，即M中的元素-1与N中的元素有4种对应方法；

　　第二步，考察x=0的象，当x=0时，为奇数，故只有2种取法（=3或=5），即M中的元素0与N中的元素有2种对应方法；

　　第三步，考察x=1的象，当x=1时，为奇数，故可为奇数也可为偶数,可取N中任一数值，即M中的元素1与N中的元素有4种对应方法，于是由分步计数原理可知，映射共有4×2×4=32个。

　　例3、在中有4个编号为1，2，3，4的小三角形，要在每一个小三角形中涂上红、蓝、黄、白、黑五种颜色中的一种，使有相邻边的小三角形颜色不同，共有多少种不同的涂法？

　　解：

根据题意，有相邻边的小三角形颜色不同，但“对角”的两个小三角形可以是相同颜色，于是考虑以对角的小三角形1、4同色与不同色为标准分为两类，进而在每一类中分步计算。

　　第一类：

1与4同色，则1与4有5种涂法，2有4种涂法，3有4种涂法，　故此时有N1=5×4×4=80种不同涂法。

　　第二类：

1与4不同色，则1有5种涂法，4有4种涂法，2有3种涂法，3有3种涂法，故此时有N2=5×4×3×3=180种不同涂法。

　　综上可知，不同的涂法共有80+180=260种。

　　点评：

欲不重不漏地分类，需要选定一个适当的分类标准，一般地，根据所给问题的具体情况，或是从某一位置的特定要求入手分类，或是从某一元素的特定要求入手分类，或是从问题中某一事物符合条件的情形入手分类，或是从问题中有关事物的相对关系入手分类等等。

　　例4、将字1、2、3、4填入标号为1、2、3、4的四个方格里，每格填一个数，则每个方格的标号与所填数字均不相同的填法有（　　）　A.6种　　　　　　B.9种　　　　C.11种　　　　D.23种

　　解法一（采用“分步”方法）：

完成这件事分三个步骤。

　　第一步：

任取一个数字，按规定填入方格，有3种不同填法；

　　第二步：

取与填入数字的格子编号相同的数字，按规定填入方格，仍有3种不同填法；

　　第三步：

将剩下的两个数字按规定填入两个格子，只有1种填法；

　　于是，由分步计数原理得，共有N=3×3×1=9种不同填法。

　　解法二：

（采用“列举”方法）：

从编号为1的方格内的填数入手进行分类。

　　第一类：

编号为1的方格内填数字2，共有3种不同填法：

2

4

1

3

2

1

4

3

2

3

4

1

　　第二类：

编号1的方格内填数字3，也有3种不同填法：

3

1

4

2

3

4

1

2

3

4

2

1

　　第三类：

编号为1的方格内填数字4，仍有3种不同填法：

4

1

2

3

4

3

1

2

4

3

2

1

于是由分类计数原理得共有N=3+3+3=9种不同填法，应选B

　　解法三（间接法）：

将上述4个数字填入4个方格，每格填一个数，共有N1=4×3×2×1=24种不同填法，其中不合条件的是　

（1）4个数字与4个格子的编号均相同的填法有1种；　

（2）恰有两个数字与格子编号相同的填法有6种；

　　（3）恰有1个数字与格子编号相同的填法有8种；　因此，有数字与格子编号相同的填法共有N2=1+6+8=15种

　　于是可知，符合条件的填法为24-15=9种。

　　点评：

解题步骤的设计原则上任意，但不同的设计招致计算的繁简程度不同，一般地，人们总是优先考虑特殊元素的安置或特殊位置的安排，以减少问题的头绪或悬念。

　　当正面考虑头绪较多时，可考虑运用间接法计算：

不考虑限制条件的方法种数—不符合条件的方法种数=符合条件的方法种数。

　　在这里，直接法中的“分析”与间接法主体的“分类”，恰恰向人们展示了“分步”与“分类”相互依存、相互联系的辩证关系。

　　例5、用数字0，1，2，3，4，5组成无重复数字4位数，其中，必含数字2和3，并且2和3不相邻的四位数有多少个？

　　解：

注意到这里“0”的特殊性，故分两类来讨论。

　　第一类：

不含“0”的符合条件的四位数，首先从1，4，5这三个数字中任选两个作排列有种；进而将2和3分别插入前面排好的两个数字中间或首尾位置，又有种排法，于是由分步计数原理可知，不含0且符合条件的四位数共有=36个。

　　第二类：

含有“0”的符合条件的四位数，注意到正面考虑头绪较多，故考虑运用“间接法”：

首先从1，4，5这三个数字中任选一个，而后与0，2，3进行全排列，这样的排列共有个。

　　其中，有如下三种情况不合题意，应当排险：

（1）0在首位的，有个；　

（2）0在百位或十位，但2与3相邻的，有个

　　（3）0在个位的，但2与3相邻的，有个

　　因此，含有0的符合条件的四位数共有=30个

　　于是可知，符合条件的四位数共有36+30=66个

　　点评：

解决元素不相邻的排列问题，一般采用“插空法”，即先将符合已知条件的部分元素排好，再将有“不相邻”要求的元素插空放入；解决元素相邻的排列问题，一般采用“捆绑法”，即先将要求相邻的元素“捆绑”在一起，作为一个大元素与其它元素进行排列，进而再考虑大元素内部之间的排列问题。

　　例6、某人在打靶时射击8枪，命中4枪，若命中的4枪有且只有3枪是连续命中的，那么该人射击的8枪，按“命中”与“不命中”报告结果，不同的结果有（　　）

　　A.720种　　　　B.480种　　　　C.24种　　　　D.20种

　　分析：

首先，对未命中的4枪进行排列，它们形成5个空挡，注意到未命中的4枪“地位平等”，故只有一种排法，其次，将连中的3枪视为一个元素，与命中的另一枪从前面5个空格中选2个排进去，有种排法，于是由乘法原理知，不同的报告结果菜有种

　　点评：

这里的情形与前面不同，按照问题的实际情况理解，未命中的4枪“地位平等”，连续命中的3枪亦“地位平等”。

因此，第一步排法只有一种，第二步的排法种数也不再乘以。

解决此类“相同元素”的排列问题，切忌照搬计算相同元素的排列种数的方法，请读者引起注意。

　　例7、

（1）　　　　　　　　　　　　；

（2）若，则n=　　　　　　　　　　　　；

　　（3）　　　　　　　　　　　　　　；

　　（4）若，则n的取值集合为　　　　　　　　　　　　；

　　（5）方程的解集为　　　　　　　　　　　　；

　　解：

（1）注意到n满足的条件

∴原式==

（2）运用