两自由度系统的振动.docx
《两自由度系统的振动.docx》由会员分享,可在线阅读,更多相关《两自由度系统的振动.docx(16页珍藏版)》请在冰豆网上搜索。
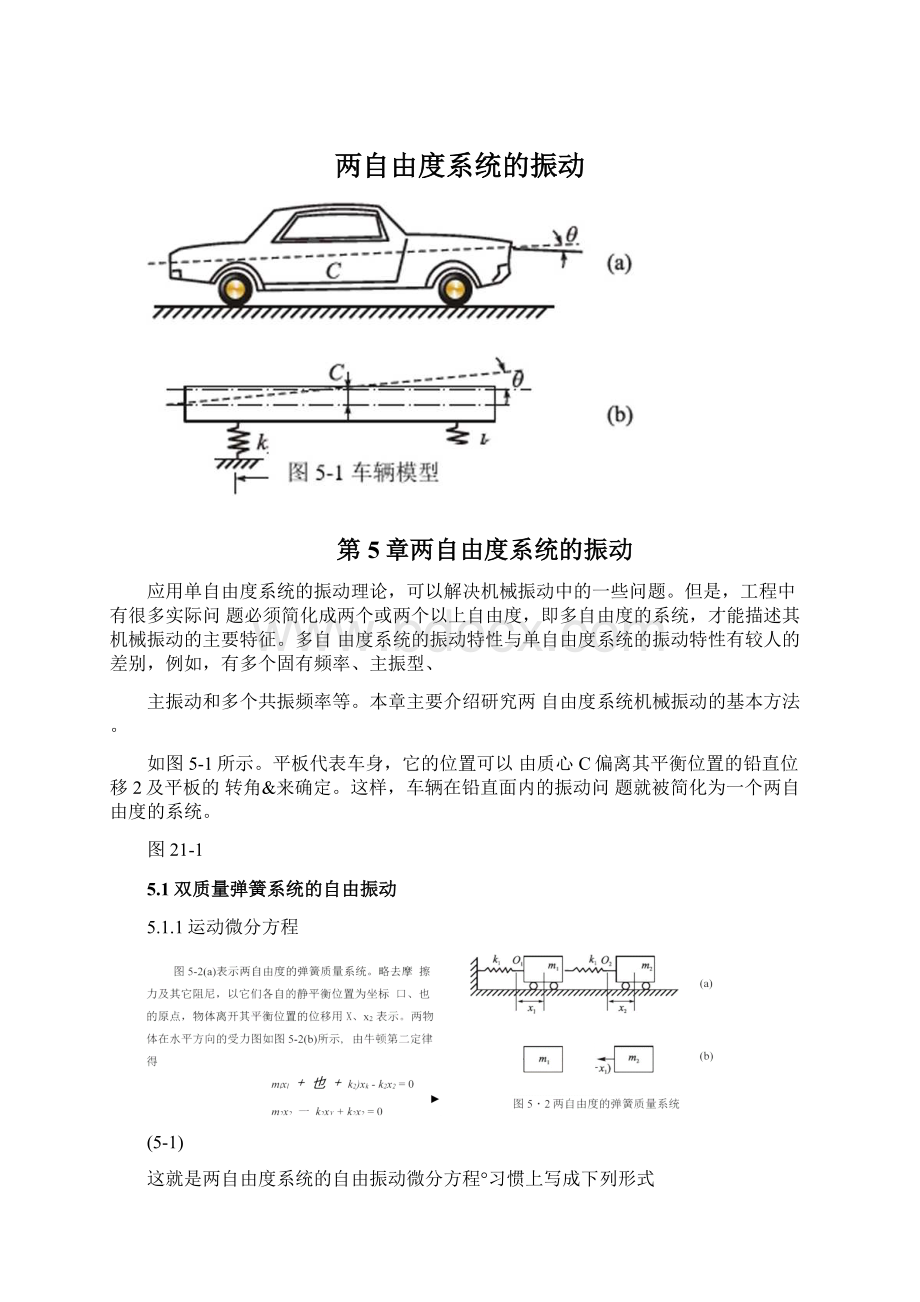
两自由度系统的振动
第5章两自由度系统的振动
应用单自由度系统的振动理论,可以解决机械振动中的一些问题。
但是,工程中有很多实际问题必须简化成两个或两个以上自由度,即多自由度的系统,才能描述其机械振动的主要特征。
多自由度系统的振动特性与单自由度系统的振动特性有较人的差别,例如,有多个固有频率、主振型、
主振动和多个共振频率等。
本章主要介绍研究两自由度系统机械振动的基本方法。
如图5-1所示。
平板代表车身,它的位置可以由质心C偏离其平衡位置的铅直位移2及平板的转角&来确定。
这样,车辆在铅直面内的振动问题就被简化为一个两自由度的系统。
图21-1
5.1双质量弹簧系统的自由振动
5.1.1运动微分方程
(5-1)
这就是两自由度系统的自由振动微分方程°习惯上写成下列形式
(5-2)
壬I+axY一bx2=0
x2-cxL+dx2=0
5.1.2固有频率和主振型
或写成以卜•的矩阵形式
将式(5・4)代入式(5・2),可得代数齐次方程组
保证式(5・5)具有非零解的充分必要条件是式(5・5)的系数行列式等于零,即
展开后为
(5-6)
p4一(d+d)“,+ad-he=0
式(5・6)唯一确定了频率"满足的条件,通常称为频率分程或特征方程。
它是"'的二次代数方程,它
的两个特征根为
由于式(5・7)确定的卩‘的两个正实根仅取决于系统本身的物理性质,与运动的初始条件无关,因此"
称为系统的固有频率。
较小的一个称为第一阶固有频率,较大的一个称为第二阶固有频率。
5.2.2主振型
将固有频率0和pi分别代入式(5・5)的任一式,可得到对应于它们的振幅比
(5-8)
1人⑴bd-p[
4卩a_p:
c
y=—i—=二=
2硏bd-p\
以上二式说明,虽然振幅的人小与振动的初始条件有关,但当系统以任一阶固有频率作同步谐振动时,振幅比却和固有频率一样只决定于系统本身的物理性质。
同时联系到式(5-3)不难看出两个质量块任意瞬时位移的比值也同样是确定的,并且等于振幅比,即:
其它各点的位移则都可以由y和心所决定。
这样在振动过程中,系统各点位移的相对比值都可由振幅比确定。
也就是说,振幅比决定了整个系统的振动形态,因之称为主振型。
与戸对应的振幅比-称为第一阶主振型,与几对应的振幅比—称为第二阶主振型。
将式(5・7)中的门、门之值带入式(5-8),得
这表明,系统以频率P]振动时,质量〃"与〃匕按同一方向运动;以频率几振动时,总是按相反的
方向运动。
系统以某一阶固有频率按其相应的主振型运动,称为系统的主振动。
第一阶主振动为
上式可以写成如下的矩阵形式,即
式中Af,斗込q”冬由运动的初始条件确定。
所以一般情况下,系统的自由振动是两个不同频率的主振动的叠加,其结果不一定是简谐振动。
例5-1试求图5・3(a)所示两个自由度系统振动的固有频率和主振型。
己知各弹簧的弹簧常量匕
所以
图54振型图
(3)求主振型
将加、p;分别代入式(5・26),得
「空—直—丄
1A”b0.732
q卩a-p;1
V->=—=—==一
・A{2)b2.732
主振型为
系统的振型图如图54所示。
图(a)表明在第一主振型中二物体的振动方向是相同的;图(b)表明在第二主振型中二者的振动方向是反相的,并且弹簧上的A点是不动的,这样的点称为节点。
例5・2在图示5・3所示系统中,已知巾=叫=m,钉=虬=匕k?
=4k,求该系统对以下两组
初始条件的响应:
(1)/=0,Xio=lcm,x2Q=x10=x2Q=0:
(2)/=0,x10=lcm,
-V-»q=—lcm^大io=大2o=0o
解:
系统的的运动微分方程分别为
mxi+5kX]一4kx2=0
mx2一4g+5kx2=0
若写成(5・2)的标准形式,则
所以
解出,=9—om■m
对应的两个主振型为
将初始条件
(1)代入式(5-10),解得
x10=A[l)sina】+A[2)snia2=1x2Q=v/Fsnia1+v2A[2)sma2=0x10=A^l)pkcosa1+A[2)p2cosa2=0x2Q=A^1)v1p1cosa1+A^2)v2p2cosa2=0
因此,皆T卅冷,亡,冬弓
所以
这表明,其响应为频率门、化的两种主振动的线性组合。
再将初始条件
(2)代入式(5-10),得
皆"矿=1,8专
所以
这表明,由于初始位移之比等于该系统的第二振幅比,因此,系统按第二主振型以频率力作谐振动。
5.2拍振现象
形成两自由度系统。
图5・5(a)表示两个摆长,质量相同的单摆,中间以弹簧相连,
图5-5双摆拍振
取$、乞表示摆的角位移,逆钟向转动为正,每个摆的受力如图5・5(b)o根据刚体绕定轴转动方
程,当乞、久角位移很小时,得到摆做微小振动的微分方程
m「匕=-inglB1+ka2(02-0J,ml262=-mglB2-ka2(B2-0J
用与前面类似的分析方法,得到系统的第一阶和第二阶固有频率为
系统的第一阶和第二阶主振型为
于是得到第一主振动
q⑴=少)sin(M+aJ,0^=®⑴sin(/H+aJ
第二主振动
即=&
(2)sin(/?
2r+cr2),=-0
(2)siii(/?
2r+ct2)
在任意初始条件下,系统振动的一般解
©=曙+0j2)=0⑴sin(/?
/+a)+0{2)sin(pJ+a2)
02=0屮+町丿=0(l)sin(”』+a)-®Esin(“J+aJ
如果初始条件是:
r=0时,9^0)=90,02(0)=01(0)=02(0)=0>代入上式得到
0⑴=(9⑺=L&,a.=a,=—
201-2因此得到双摆作自由振动的规律
0000
0{=—(cospj+cosp2t),Q2=—(cos/?
/-cosp2t)
22
如果弹簧的刚度R很小,即
竺<<5
ml2I
这时p^p2相差很少,将上式写成
=00cos
Pi+At
2
令△p=卩?
一Plpa=则上式为
乙
91=Oocos—,Q2=90sni—^-/siiipat
2
这表明,两个摆的运动可以看作是频率为几的简谐运动,但其振幅不是常数,而是缓慢变化的简谐
函数e°gs牛和&osin¥"这种现象称为拍振。
称为拍的周期。
由于△〃较小,所以拍的周期一般较长。
此外,两个拍振之间相位角差为扌,就是
说,当f=0时,左边的摆以%开始摆动,右边的不动:
随后,左边摆的振幅逐渐减小,右边摆的振
幅逐渐增人。
当t=-TB时,左边的摆停止,右边的摆达到%,再经过丄几,即f=7;时,右边的22
摆停止,左边的摆达到%。
这种循坏,每隔一个拍振周期重复一次。
可以看到,两个摆的动能也从
一个摆传递到另一个摆,循环传递,使它们持续地振动。
图5-6双摆拍振q=cos0.05/cos2.05/,02=sin0.05/sin2.05/的时间历程
5.3坐标的耦联
5.3」耦联与非耦联
如前所述,一般情况下两自由度系统的振动微分方程组的形式为
乙+ax{一hx2=0
x2-cxL+dx2=0
可见在质点m和〃匕的运动方程式中,都含有坐标X和小。
这表明,两个质点的运动不是互相独立的,它们彼此受另一个质点的运动的影响。
像这样表示振动位移的两个以上坐标出现在同一个运动方程式中时,就称这些坐标之间存在静力耦联或弹性耦联。
另外,与上式情况不同,当一个微分方程式中出现两个以上的加速度项时,称为在坐标之间有
动力耦联或惯性耦联C
某个系统中是否存在耦联取决于用以表示运动的坐标的选择方法,而与系统本身的特性无关。
一般说来,为了表示多质点系的运动状态,可以选用的独立坐标系,即广义坐标,可能有几种。
根据选择坐标的不同,系统可以是静力耦联,动力耦联、静力兼动力耦联,或非耦联的(即完全无耦联的)。
5.3.2主坐标
从上一节的分析可以知道,两质点无阻尼系统的运动方程式以中⑴,①⑴为广义坐标可写成如下最一般的形式
+/%厶+K曲+匕皿=0IM曲+M22q2+心皿+Kg=0/
式中M”和K”(迸/)分别表示动力和静力耦联项。
然而,如果坐标选择得当,可使式(A)中的耦联项为M?
=0,Ky=0(jH))。
即总是可以使微分方程式不联立,在每个式子中分别只含一个未知数而与另一未知数无关。
如果能得到这种独立的运动方程式,则作为方程解求岀的系统各个分量的运动与其它各分量的运动无关,分别作具有各自固有的振幅、频率和相位的单自由度振动,即谐和振动,问题就大大简化了。
这种经特别选择的、可使方程式写成既无动力耦联又无静力耦联形式的坐标称为主坐标。
例5-7试由双摆作微小摆动的微分方程,寻求系统的主坐标。
解:
双摆作微小摆动的微分方程为
―罕小”窘=0
ml"Iml-
将以上两式相加、相减便得到
&+0?
+孚(Oj+%)=o"+和鴛畑7)=0
令屮1=%+%,屮2=°1一°「上式变为
V1+J屮]=0屮2+(今+学)屮2=°
Iml-
可见,屮”屮三就是系统的主坐标,所以该系统的两个固有频率为
5.4双质量弹簧系统的受迫振动
在图5-3所示的两自由度系统力学模型中,若两个物块受到激振力的作用,
F&)=sinet,&(')=&sm〃,可列出该系统的受迫振动微分方程,其矩阵形式为
mlxl+伙]+k2)xl一k2x2=sin6X
nt2x2_&站+伙三+k^)x2=F2sincot
令
匕+krJkrh+人F.Fr
g=__•b=rc=亠,d=__・力=」,匸=亠
〃”m2m2〃”m2
则得
x.+ax{一bx^=人sina
f(5-15)
x2-exL+dx2=/2sin6X
这是二阶线性常系数非齐次微分方程组。
由微分方程理论知,其解由对应的齐次方程组的通解与该非齐次方程组的特解组成。
前者为系统的自由振动,和单自由度系统一样,由于阻尼的存在,它将在较短时间内衰减掉,后者为系统的受迫振动,不随时间衰减。
当自由振动部分衰减了以后,
式中△(°')=(°一°')(〃一°2)-bc=(“;一°2)(加一°三),其中0、"2为系统的两个固有频率(见”;,P;的表达式)。
于是得出结论:
在简谐干扰力作用下,两自由度无阻尼的线性振动系统的受迫振动是以干扰力频率为其频率的简谐振动,其振幅由式(5-18)确定。
式(5-18)表明,受迫振动的振幅大小不仅和干扰力的幅值人小Fl、尺有关,而且和干扰力的频
率e有关。
特别是当。
=门或少=力时,即当干扰力的频率等于振动系统的固有频率时,振幅5、B2将会无限地増人,发生共振。
与单自由度振动系统不同,两自由度系统一般有两个固有频率,因此,可能出现两次共振。
由式(5-18)nf得
(5-19)
这说明对于确定的激振力的幅值和频率,振幅比同样是确定值,也就是说系统有确定的振型。
当干扰力的频率。
等于第一阶固有频率时,
+bf2
将方程(5・8)第一式中二^的分子分母同乘以八,的分子分母同乘以办,根据比例式相加法b…d_巧
则得到
v_c
1d-p~b(d-p~)/i+bf2I§丿护几
同理,当。
=力时,则有这表明,系统在任何一个共振频率下的振型就是相应的主振型。
振动测量中常利用这一规律来测量系统的固有频率,并根据共振时系统的振动形态来判断该固有频率的阶次。
例图5-3所示系统中已知各弹簧的弹簧常量k,=k2=k.k、=2k;物体的质量m2=2ma若在质量“上作用一激振力(/)=sin6X而耳(r)=0。
(1)求系统的响应;
(2)计算
共振时的振幅比;(3)作幅频特性曲线。
g八、2k.kk■3khzrk->5k
(1)d=9b=—,C=9d=,所以9p;=—O
inm2m2mm"2m
所以
(al)
(a2)
B_(莎)万_(3k_2〃s')F]
1(£-°2)(竺_°2)(k-mco2)(5—2mar)
m2m
B=2mm=里
2{L-co-)(21-co2)伙一"2)(5k-2ma)2)
m2m
故系统的响应为
Qk一2mco2)Fl
x.=;sincot
(k一mco2)(5k-2mco2)
kF、
x2=;——sincot
(k一mco^)(5R-2m)
(2)生=—-—°当宀p:
丄时,冬=l=m当co2=p;=—时,冬=_丄=心。
B]3k—2加mB]2m2「
(3)将振幅的表达式(al)、(a2)改写成如下无量纲形式
图5-7给出的无量纲振幅%/灯(兰色)、%〃灯(红色)和无量纲频率%】之间的关系曲线表明有两次共振。
每次共振时,两个质量块的振幅都同时达到最人值。
当激励频率为阿乔时,叫的振幅为零,这种现象通常称为反共振。
当激励频率阿莎时,两个质量块的运动方向相同:
当激励频率QJ3时2m时,两个质量块的运动方向相反。
当co»p2时,两个质量块的振幅都非常小而趋于零。
5.5动力减振器
上节已经指出,对一个两自由度系统,当其中的一个质量块受到外界激励时,它却有可能不动而使另一个质量块运动。
根据这个原理,可以制成工程上常用的动力减振器。
图5-8所示梁上装有一电动机,运转时由于转子的偏心而诱发强迫振动。
这可用质量为弹簧刚度为人的单自由度系统的受迫振动来描述。
在某一确定的电机转速下可能由于共振而引起强烈振动。
为此在梁上附加一个质量为加「弹簧刚度为紅的弹簧质量系统,从而构成了一个两自由度
的系统。
图5・8动力减振器
根据上节的讨论,此系统的振动微分方程为:
加曲+&+k2)xi_^2X2=片sin创
m2x2一k2xY+k2x2=0
其强迫振动的振幅为
{d-co^n
△3)
△(少)
式中
)=(q_a)2)(d-co2)-be9
匕1,b=邑,C=j,f占,
“叫
k
不难看出,当Q,=d=乂时,
E=o
B,=—
bkr
■丿
这就是说,主系统不动而减振器以”=BrSinm=-2sin劲作受迫振动。
减振器弹簧在下端受到
的作用力为
k2x2=_耳sin血
在任何瞬时,都与激振力F,SHIcot相平衡,因此使主系统的振动转移到减振器上来。
图5-9给出了&=铤严=1,“=佶=1时无量纲振幅%仏)和无量纲频率滋丽万之间的关系曲线。
=1时,%/匕)=°。
当考虑系统的阻尼时,主系统不是完全不
动,而是以较小的振幅振动。
此外还可以看出在。
=阿石附近有两个共振峰值。
如果加「灯选择不当,可能引起新的共振。
为此必须控制附加动力减振器后的两自由度系统的固有频率。
5.6阻尼对强迫振动的影响
为了把问题简化,以上的分析都没有考虑系统的阻尼。
本节以图5-10所示系统为例,讨论阻尼对两自由度系统受迫振动的影响。
这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。
其运动微分方程为
mlxi+(人+k2)xL_k2x2+c(九_攵三)=耳sin曲
m2x2-k2x{+k2x2一c(.*i-)=0
(5-20)仍只考虑稳态运动。
若利用复指数形式,则激振力为F严,而稳态运动的形式为
x2=B2ej{M~^
(5-21)
将(5-21)代入(5-20)后可解出耳、比。
下面只以主质量M的振幅$进行讨论。
其无量纲表达式为
(A2-a2)2+(2^L)2
疋%)Y[/以'a?
-(22-&')]'+(2飙)'(,-1+//A2)2
(5-22)
式中
「—mb—-
叫PO22k,/2
“=—,a=——,Poi=人,Poz
加]p0l/®
A=%0/加%'c'=2叫仏
可见对于确定的“和a,无量纲振幅寿-是几和纟的函数,这与单自由度受迫振动的情况一样。
图5-10有阻尼的双弹簧质量系统
图5-11对应“=丄和a=1的幅频特性曲线。
疳=0为无阻尼的情况;§=s相当于和®刚性连
接,所以幅频特性曲线与单自由度受迫振动的幅频特性曲线相同。
不难看出,阻尼会使共振附近的振幅显著减小,但激振频率C0«p{或0>>必时,阻尼对振幅的影响很小。
此外,(5-22)所代表的响应曲线,无论纟的值如何都通过S与T两点。
这表明对于这两点对应的频率,主质量的振幅与阻尼无关。
图5J1考虑阻尼时动力减振器的幅频特性曲线
(注:
范文素材和资料部分來自网络,供参考。
只是收取少量整理收集费用,请预览后才下载,期待你的好评与关注)