圆的面积和圆柱体体积的变式练习两课时导学案.doc

圆的面积和圆柱体体积的变式练习两课时导学案.doc

《圆的面积和圆柱体体积的变式练习两课时导学案.doc》由会员分享，可在线阅读，更多相关《圆的面积和圆柱体体积的变式练习两课时导学案.doc（4页珍藏版）》请在冰豆网上搜索。

圆的面积和圆柱体体积的变式练习（两课时导学案）

一、简答

怎样计算圆的周长？

怎样计算圆的面积？

怎样计算圆柱体的体积？

二、想一想，画一画。

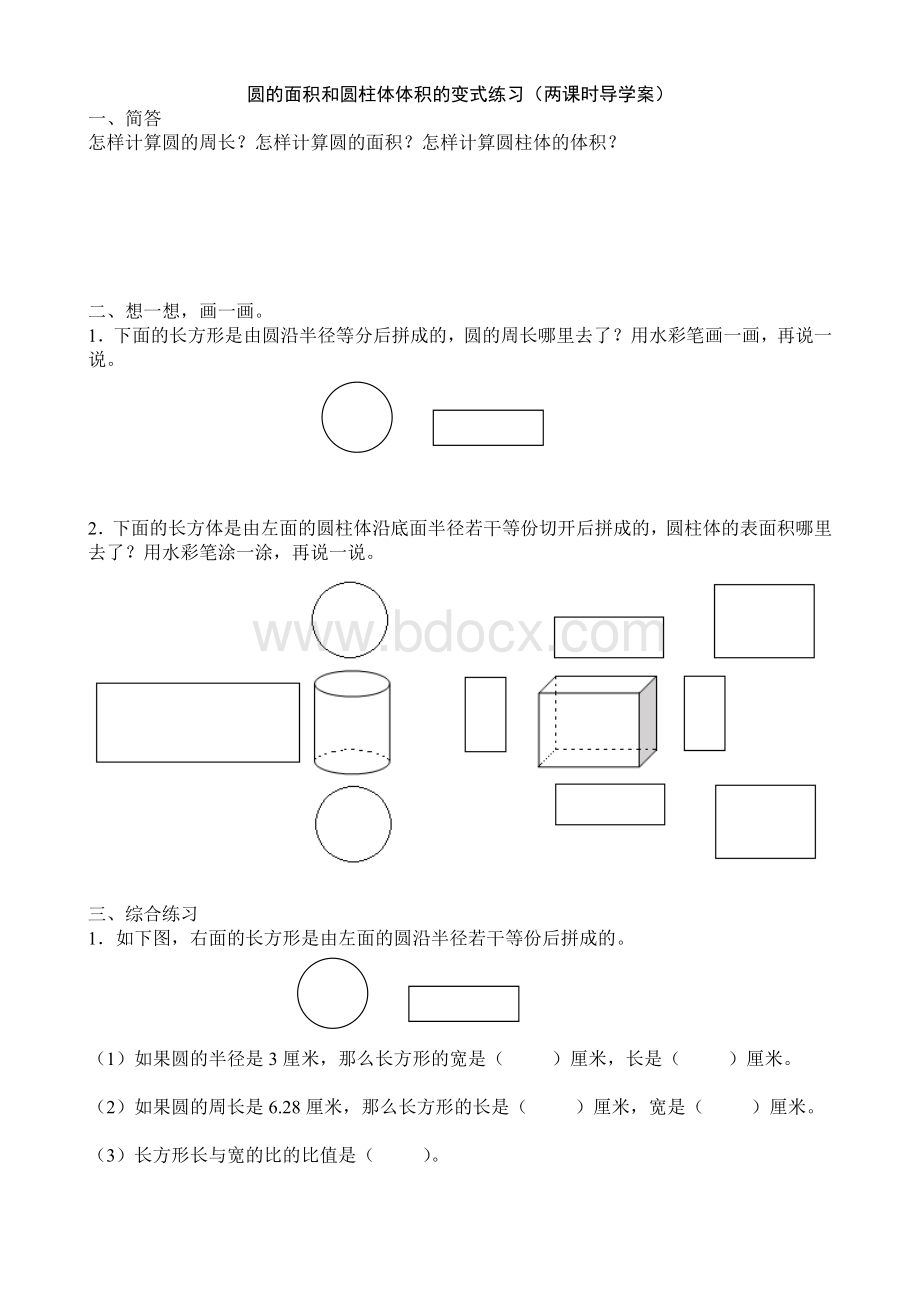
1．下面的长方形是由圆沿半径等分后拼成的，圆的周长哪里去了？

用水彩笔画一画，再说一说。

2．下面的长方体是由左面的圆柱体沿底面半径若干等份切开后拼成的，圆柱体的表面积哪里去了？

用水彩笔涂一涂，再说一说。

三、综合练习

1．如下图，右面的长方形是由左面的圆沿半径若干等份后拼成的。

（1）如果圆的半径是3厘米，那么长方形的宽是（）厘米，长是（）厘米。

（2）如果圆的周长是6.28厘米，那么长方形的长是（）厘米，宽是（）厘米。

（3）长方形长与宽的比的比值是（）。

2．如下图，右面的长方体是由左面的圆柱沿底面半径若干等份切开后拼成的。

（1）如果圆柱体的底面积是3.14平方厘米，侧面积是18.84平方厘米，那么长方体的底面积是（）平方厘米，前面的面积是（）平方厘米。

（2）如果圆柱体的底面半径是2厘米，高是6厘米，那么长方体右侧面的面积是（）平方厘米。

（3）如果圆柱体的底面半径是1厘米，高是3厘米，那么圆柱体切拼成长方体后，表面积增加了（）平方厘米。

3．如下图，长方形是由圆沿半径等分剪开后拼成的。

如果阴影部分的面积是12平方厘米，这个圆的面积是（）平方厘米。

4．把圆柱体沿底面半径等分切开后拼成长方体，结果表面积增加了40平方厘米。

已知圆柱体的高是10厘米，那么圆柱体的体积是（）立方厘米。

5．如下图，右面的长方形是由左面的圆沿半径若干等份后拼成的。

如果圆的周长是15.7厘米，长方形的周长是（）厘米；如果长方形的长是6.28厘米，圆的面积是（）平方厘米。

6．把一个圆柱体切割后拼成一个近似的长方体。

如果这个长方体如右图所示摆放，长6厘米，

高6.28厘米，原来圆柱体的体积是（）

立方厘米，切拼后的长方体表面积是（）

平方厘米。

课题：

圆的面积与圆柱体积的综合变式练习

教学目标：

深度理解“化曲为直”转化的原理、方法，在此基础上尝试在变式中分析破解相关的练习；通过计算简洁、思考灵活、有相当思维含量的练习体验数学学习中的思维之妙。

过程：

一、回顾转化的基本原理

1．静心观察，清晰回顾。

（1）圆转变为长方形。

学生操作，抚摸圆的周长与面积；抚摸长方形的周长与面积。

（2）圆柱转变为长方体。

分组实际操作。

（3）标准化归图。

2．对“转变”的梳理。

（1）圆的周长哪里去了？

（手指学具描述；配展开图，用彩色笔描画）把圆转变为长方形的过程中，什么变了，什么没有变？

突出两条宽。

（2）圆柱的表面积哪里去了？

（手指学具描述；配展开图，上底面、下底面、侧面依次展开，分别化为长方体的上面、下面、前面和后面）把圆柱转变为圆柱体的过程中，什么变了，什么没有变？

突出两个侧面。

二、实际演练

1．第一层面

（1）圆与长方形

如下图，右面的长方形是由左面的圆沿半径若干等份后拼成的。

①如果圆的半径是3厘米，那么长方形的宽是（）厘米，长是（）厘米。

②如果圆的周长是6.28厘米，那么长方形的长是（）厘米，宽是（）厘米。

③长方形长与宽的比的比值是（）。

（2）圆柱与长方体

如下图，右面的长方体是由左面的圆柱沿底面半径若干等份切开后拼成的。

①如果圆柱体的底面积是3.14平方厘米，侧面积是18.84平方厘米，那么长方体的底面积是（）平方厘米，前面的面积是（）平方厘米。

②如果圆柱体的底面半径是2厘米，高是6厘米，那么长方体右侧面的面积是（）平方厘米。

③如果圆柱体的底面半径是1厘米，高是3厘米，那么圆柱体切拼成长方体后，表面积增加了（）平方厘米。

2．第二层面

①如下图，长方形是由圆沿半径等分剪开后拼成的。

如果阴影部分的面积是12平方厘米，这个圆的面积是（）平方厘米。

②把圆柱体沿底面半径等分切开后拼成长方体，结果表面积增加了40平方厘米。

已知圆柱体的高是10厘米，那么圆柱体的体积是（）立方厘米。

3．第三层面

①如下图，右面的长方形是由左面的圆沿半径若干等份后拼成的。

已知圆的周长是15.7厘米，长方形的周长是（）厘米。

如果长方形的长是6.28厘米，圆的面积是（）平方厘米。

②把一个圆柱体切割后拼成一个近似的长方体。

如果这个长方体如右图所示摆放，长6厘米，

高6.28厘米，原来圆柱体的体积是（）

立方厘米，切拼后的长方体表面积是（）

平方厘米。