现代数字信号处理仿真作业.docx
《现代数字信号处理仿真作业.docx》由会员分享,可在线阅读,更多相关《现代数字信号处理仿真作业.docx(26页珍藏版)》请在冰豆网上搜索。
现代数字信号处理仿真作业
现代数字信号处理仿真作业
1.仿真题3.17
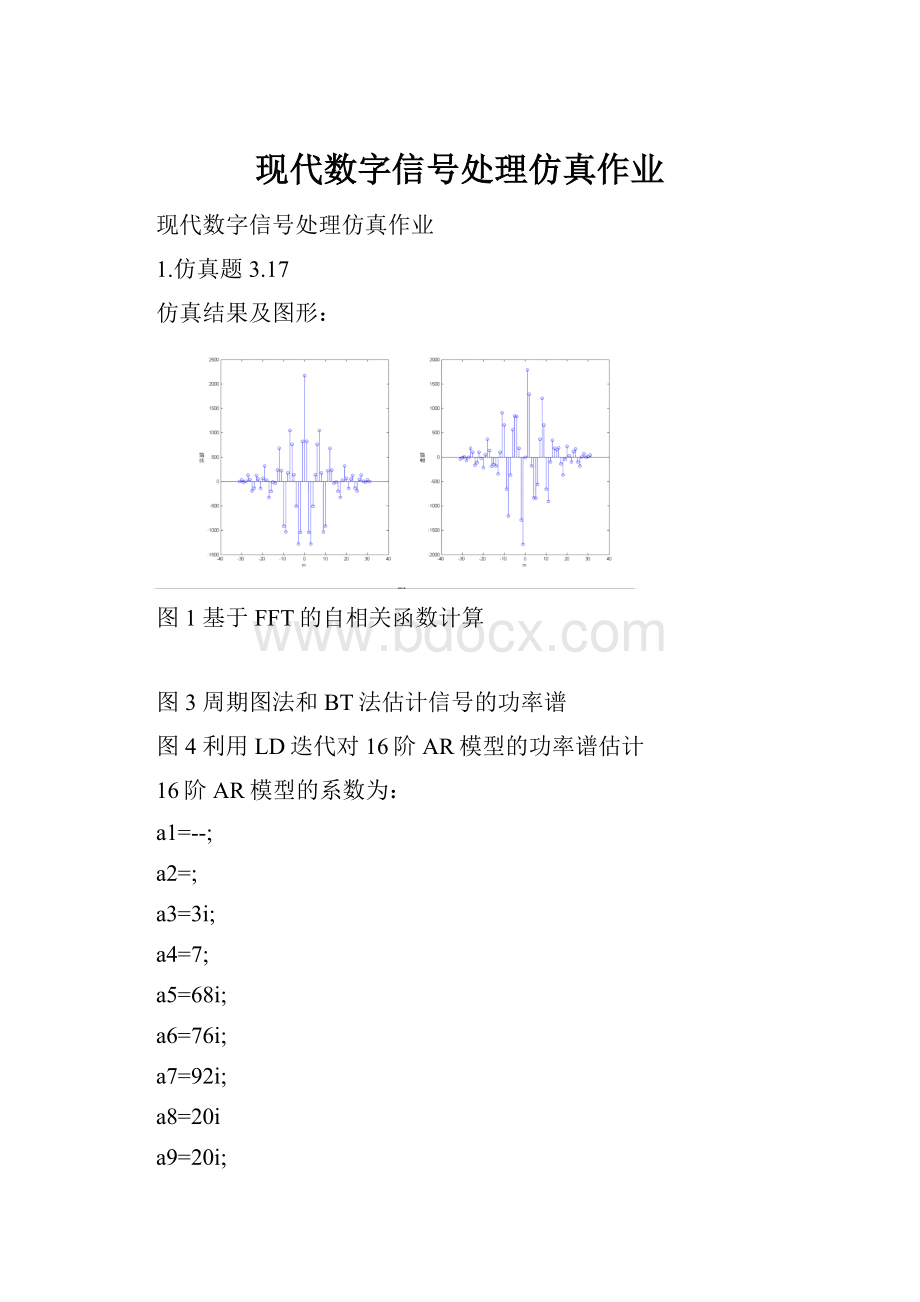
仿真结果及图形:
图1基于FFT的自相关函数计算
图3周期图法和BT法估计信号的功率谱
图4利用LD迭代对16阶AR模型的功率谱估计
16阶AR模型的系数为:
a1=--;
a2=;
a3=3i;
a4=7;
a5=68i;
a6=76i;
a7=92i;
a8=20i
a9=20i;
a10=23i;
a11=710i;
a12=49i;
a13=83i;
a14=24i;
a15=21i;
a16=3i.
仿真程序(3_17):
clearall
clc
%%产生噪声序列
N=32;%基于FFT的样本长度
%N=256;%周期图法,BT法,AR模型功率谱估计的长度
vn=(randn(1,N)+1i*randn(1,N))/sqrt
(2);
%%产生复正弦信号
f=[0.150.170.26];%归一化频率
SNR=[303027];%信噪比
A=10.^(SNR./20);%幅度
signal=[A
(1)*exp(1i*2*pi*f
(1)*(0:
N-1));%复正弦信号
A
(2)*exp(1i*2*pi*f
(2)*(0:
N-1));
A(3)*exp(1i*2*pi*f(3)*(0:
N-1))];
%%产生观察样本
un=sum(signal)+vn;
%%利用3.1.1的FFT估计
Uk=fft(un,2*N);
Sk=(1/N)*abs(Uk).^2;
r0=ifft(Sk);
r1=[r0(N+2:
2*N),r0(1:
N)];
%%
r2=xcorr(un,N-1,'biased');
%画图
k=-N+1:
N-1;
figure
(1)
subplot(1,2,1)
stem(k,real(r1))
xlabel('m');ylabel('实部');
subplot(1,2,2)
stem(k,imag(r1))
xlabel('m');ylabel('虚部');
figure
(2)
subplot(1,2,1)
stem(k,real(r2))
xlabel('m');ylabel('实部');
subplot(1,2,2)
stem(k,imag(r2))
xlabel('m');ylabel('虚部');
%%周期图法
NF=1024;
Spr=fftshift((1/NF)*abs(fft(un,NF)).^2);
kk=-0.5+(0:
NF-1)*(1/(NF-1));
Spr_norm=10*log10(abs(Spr)/max(abs(Spr)));
%%BT法
M=64;
r3=xcorr(un,M,'biased');
BT=fftshift(fft(r3,NF));
BT_norm=10*log10(abs(BT)/max(abs(BT)));
figure(3)
subplot(1,2,1)
plot(kk,Spr_norm)
xlabel('w/2pi');ylabel('归一化功率谱/DB');
title('周期图法')
subplot(1,2,2)
plot(kk,BT_norm)
xlabel('w/2pi');ylabel('归一化功率谱/DB');
title('BT法')
%%LD迭代算法
p=16;
r0=xcorr(un,p,'biased');
r4=r0(p+1:
2*p+1);%计算自相关函数
a(1,1)=-r4
(2)/r4
(1);
sigma
(1)=r4
(1)-(abs(r4
(2))^2)/r4
(1);
form=2:
p%LD迭代算法
k(m)=-(r4(m+1)+sum(a(m-1,1:
m-1).*r4(m:
-1:
2)))/sigma(m-1);
a(m,m)=k(m);
fori=1:
m-1
a(m,i)=a(m-1,i)+k(m)*conj(a(m-1,m-i));
end
sigma(m)=sigma(m-1)*(1-abs(k(m))^2);
end
Par=sigma(p)./fftshift(abs(fft([1,a(p,:
)],NF)).^2);%p阶AR模型的功率谱
Par_norm=10*log10(abs(Par)/max(abs(Par)));
figure(4)
plot(kk,Par_norm)
xlabel('w/2pi');ylabel('归一化功率谱/DB');
title('16阶AR模型')
2.仿真题3.20
仿真结果及图形:
单次Root-MUSIC算法中最接近单位圆的两个根为:
对应的归一化频率为:
相同信号的MUSIC谱估计结果如下
图5对3.20信号进行MUSIC谱估计的结果
仿真程序(3_20):
clearall
clc
%%信号样本和高斯白噪声的产生
N=1000;
vn=(randn(1,N)+1i*randn(1,N))/sqrt
(2);
signal=[exp(1i*0.5*pi*(0:
N-1)+1i*2*pi*rand);%复正弦信号
exp(-1i*0.3*pi*(0:
N-1)+1i*2*pi*rand)];
un=sum(signal)+vn;
%%计算自相关矩阵
M=8;
fork=1:
N-M
xs(:
k)=un(k+M-1:
-1:
k).';
end
R=xs*xs'/(N-M);
%%自相关矩阵的特征值分解
[U,E]=svd(R);
%%Root-MUSIC算法的实现
G=U(:
3:
M);
Gr=G*G';
co=zeros(2*M-1,1);
form=1:
M
co(m:
m+M-1)=co(m:
m+M-1)+Gr(M:
-1:
1,m);
end
z=roots(co);
ph=angle(z)/(2*pi);
err=abs(abs(z)-1);
%%计算MUSIC谱
En=U(:
2+1:
M);
NF=2048;
forn=1:
NF
Aq=exp(-1i*2*pi*(-0.5+(n-1)/(NF-1))*(0:
M-1)');
Pmusic(n)=1/(Aq'*En*En'*Aq);
end
kk=-0.5+(0:
NF-1)*(1/(NF-1));
Pmusic_norm=10*log10(abs(Pmusic)/max(abs(Pmusic)));
plot(kk,Pmusic_norm)
xlabel('w/2*pi');ylabel('归一化功率谱/dB')
3.仿真题3.21
仿真结果及图形:
单次ESPRIT算法中最接近单位元的两个特征值为:
对应的归一化频率为:
仿真程序(3_21):
clearall
clc
%%信号样本和高斯白噪声的产生
N=1000;
vn=(randn(1,N)+1i*randn(1,N))/sqrt
(2);
signal=[exp(1i*0.5*pi*(0:
N-1)+1i*2*pi*rand);%复正弦信号
exp(-1i*0.3*pi*(0:
N-1)+1i*2*pi*rand)];
un=sum(signal)+vn;
%%自相关矩阵的计算
M=8;
fork=1:
N-M
xs(:
k)=un(k+M-1:
-1:
k).';
end
Rxx=xs(:
1:
end-1)*xs(:
1:
end-1)'/(N-M-1);
Rxy=xs(:
1:
end-1)*xs(:
2:
end)'/(N-M-1);
%%特征值分解
[U,E]=svd(Rxx);
ev=diag(E);
emin=ev(end);
Z=[zeros(M-1,1),eye(M-1);0,zeros(1,M-1)];
Cxx=Rxx-emin*eye(M);
Cxy=Rxy-emin*Z;
%%广义特征值分解
[U,E]=eig(Cxx,Cxy);
z=diag(E);
ph=angle(z)/(2*pi);
err=abs(abs(z)-1);
4.仿真题4.18
仿真结果及图形:
步长为0.05时失调参数为m1=0.0493;
步长为0.005时失调参数为m2=0.0047。
图6步长为0.05时权向量的收敛曲线
图7步长为0.005时权向量的收敛曲线
图8步长分别为0.05和0.005时100次独立实验的学习曲线
仿真程序(4_18):
clearall
clc
%%产生100组独立样本序列
data_len=512;
trials=100;
n=1:
data_len;
a1=-0.975;
a2=0.95;
sigma_v_2=0.0731;
v=sqrt(sigma_v_2)*randn(data_len,1,trials);
u0=[00];
num=1;
den=[1,a1,a2];
Zi=filtic(num,den,u0);
u=filter(num,den,v,Zi);%产生100组独立信号
%%LMS迭代
mu1=0.05;mu2=0.005;
w1=zeros(2,data_len,trials);w2=w1;
form=1:
100;
temp=zeros(data_len,1);
e1(:
:
m)=temp;e2(:
:
m)=temp;d1(:
:
m)=temp;d2(:
:
m)=temp;
forn=3:
data_len-1
w1(:
n+1,m)=w1(:
n,m)+mu1*u(n-1:
-1:
n-2,:
m)*conj(e1(n,1,m));
w2(:
n+1,m)=w2(:
n,m)+mu2*u(n-1:
-1:
n-2,:
m)*conj(e2(n,1,m));
d1(n+1,1,m)=w1(:
n+1,m)'*u(n:
-1:
n-1,:
m);
d2(n+1,1,m)=w2(:
n+1,m)'*u(n:
-1:
n-1,:
m);
e1(n+1,1,m)=u(n+1,:
m)-d1(n+1,1,m);
e2(n+1,1,m)=u(n+1,:
m)-d2(n+1,1,m);
end
end
t=1:
data_len;
w1_mean=zeros(2,data_len);w2_mean=w1_mean;e1_mean=zeros(data_len,1);e2_mean=e1_mean;
form=1:
100
w1_mean=w1_mean+w1(:
:
m);
w2_mean=w2_mean+w2(:
:
m);
e1_mean=e1_mean+e1(:
:
m).^2;
e2_mean=e2_mean+e2(:
:
m).^2;
end
w1_mean=w1_mean/100;%100次独立实验权向量的均值
w2_mean=w2_mean/100;
e1_100trials_ave=e1_mean/100;%100次独立实验的学习曲线均值
e2_100trials_ave=e2_mean/100;
figure
(1)
plot(t,w1(1,:
90),t,w1(2,:
90),t,w1_mean(1,:
),t,w1_mean(2,:
))
xlabel('迭代次数');ylabel('权向量')
title('步长=0.05')
figure
(2)
plot(t,w2(1,:
90),t,w2(2,:
90),t,w2_mean(1,:
),t,w2_mean(2,:
))
xlabel('迭代次数');ylabel('权向量')
title('步长=0.005')
%%计算剩余误差和失调参数
wopt=zeros(2,trials);
Jmin=zeros(1,trials);
sum_eig=zeros(trials,1);
form=1:
trials
rm=xcorr(u(:
:
m),'biased');
R=[rm(512),rm(513);rm(511),rm(512)];
p=[rm(511);rm(510)];
wopt(:
m)=R\p;
[v,d]=eig(R);
Jmin(m)=rm(512)-p'*wopt(:
m);
sum_eig(m)=d(1,1)+d(2,2);
end
sJmin=sum(Jmin)/trials;
Jex1=e1_100trials_ave-sJmin;%剩余均方误差mu1
Jex2=e2_100trials_ave-sJmin;%剩余均方误差mu2
sum_eig_100trials=sum(sum_eig)/100;
Jexfin1=mu1*sJmin*(sum_eig_100trials/(2-mu1*sum_eig_100trials));
Jexfin2=mu2*sJmin*(sum_eig_100trials/(2-mu2*sum_eig_100trials));
M1=Jexfin1/sJmin;%失调参数m1
M2=Jexfin2/sJmin;%失调参数m2
figure(3)
plot(t,e1_100trials_ave,'*',t,e2_100trials_ave)
xlabel('迭代次数');ylabel('均方误差')
legend('u1=0.05','u2=0.005')
axis([0,600,0,1])
5.仿真题5.10
仿真结果及图形:
(1)M=2时,
,求解Yule-Walker方程
可得到自相关矩阵
相应的计算程序为
r2=inv([1,-0.99;-0.99,1])*[0.93627;0];
R2=[r2
(1),r2
(2);r2
(2),r2
(1)];%M=2
(2)M=3时,
,求解Yule-Walker方程
可得到自相关矩阵为
相应的计算程序为
r3=inv([1,-0.99,0;-0.99,1,0;0,-0.99,1])*[0.93627;0;0];
R3=[r3
(1),r3
(2),r3(3);r3
(2),r3
(1),r3
(2);r3(3),r3
(2),r3
(1)];%M=3
(3)计算特征值扩展
%%特征值分解
eig_value_1=eig(R2);
eig_value_2=eig(R3);
%%特征值扩展
eig_spread_1=max(eig_value_1)/min(eig_value_1);
eig_spread_2=max(eig_value_2)/min(eig_value_2);
M=2时特征值扩展是199.0000;
M=3时特征值扩展是444.2790。
(3)根据LMS算法均方误差收敛特性,M=2时步长因子应在区间(0,0.0213)中,M=3时,步长因子应在区间(0,0.0142)之间,因此题中的步长因子不合理。
故在仿真中,M=2时采用步长因子0.001,M=3时采用步长因子0.0006.
图9500次独立实验M=2步长为0.001时权向量收敛曲线
图10500次独立实验M=3步长为0.0006时权向量收敛曲线
图11500次独立实验M=2步长为0.001时的学习曲线
图12500次独立实验M=3步长为0.0006时的学习曲线
仿真程序(5_10_4):
clearall
clc
%%产生系统输入白噪声
L=10000;
sigma_v1_2=0.93627;
form=1:
500
v(:
m)=sqrt(sigma_v1_2)*randn(L,1);
end
%%生成500组独立的AR模型信号
a1=-0.99;
form=1:
500
u(1,1,m)=v(1,m);
fork=2:
L
u(k,1,m)=-a1*u(k-1,1,m)+v(k,m);
end
end
%%LMS迭代算法
M=2;
%M=3;
mu=0.001;
%mu=0.0006;
w=zeros(L,M,500);
form=1:
500
e(1,m)=u(1,m);
uu=zeros(1,M);
w(2,:
m)=w(1,:
m)+mu*e(1,m)*uu;
uu=[u(1,m)uu(1:
M-1)];
dd=(w(2,:
m)*uu')';
e(2,m)=u(3,m)-dd;
fork=3:
L
w(k,:
m)=w(k-1,:
m)+mu*e(k-1,m)*uu;
uu=[u(k-1,1,m)uu(1:
M-1)];
dd=(w(k,:
m)*uu')';
e(k,m)=u(k,m)-dd;
end
end
%%M=2
e_mean=zeros(10000,1);
w_mean=zeros(10000,2);
form=1:
500
w_mean=w_mean+w(:
:
m);
e_mean=e_mean+e(:
m).^2;
end
w_mean=w_mean/500;
e_mean=e_mean/500;
t=1:
L;
figure
(1)
plot(t,w(:
1,100),t,w(:
2,100),t,w_mean(:
1),t,w_mean(:
2))
xlabel('迭代次数n');ylabel('抽头权值');
title('M=2,步长0.001的权向量收敛曲线')
figure
(2)
plot(t,e_mean)
xlabel('迭代次数n');ylabel('MSE');title('M=2,步长0.001的学习曲线')
%%M=3
e_mean=zeros(10000,1);
w_mean=zeros(10000,3);
form=1:
500
w_mean=w_mean+w(:
:
m);
e_mean=e_mean+e(:
m).^2;
end
w_mean=w_mean/500;
e_mean=e_mean/500;
t=1:
L;
figure
(1)
plot(t,w(:
1,100),t,w(:
2,100),t,w(:
3,100),t,w_mean(:
1),t,w_mean(:
2),t,w_mean(:
3))
xlabel('迭代次数n');ylabel('抽头权值');
title('M=3,步长0.0006的权向量收敛曲线')
figure
(2)
plot(t,e_mean)
xlabel('迭代次数n');ylabel('MSE');title('M=2,步长0.0006的学习曲线')
6.仿真题6.13
仿真结果及图形:
滤波器抽头个数为4时
图13M=4时的MVDR谱
图14M=4时基于奇异值分解的MVDR谱
从上面两图可以看出,M=4时并没有将3个频点分辨出来,增加滤波器阶数可以解决此问题,因此当M=20时仿真结果如下两图所示:
图15M=20时的MVDR谱
图16M=20时基于奇异值分解的MVDR谱
仿真程序(6_13):
clearall
clc
%%产生观测信号
M=4;
%M=20;
N=1000;
f=[0.10.250.27];
SNR=[303027];
sigma=1;
Am=sqrt(sigma*10.^(SNR/10));
t=linspace(0,1,N);
phi=2*pi*rand(size(f));
vn=sqrt(sigma/2)*randn(size(t))+1i*sqrt(sigma/2)*randn(size(t));
Un=vn;
fork=1:
length(f)
s=Am(k)*exp(1i*2*pi*N*f(k).*t+1i*phi(k));
Un=Un+s;
end
Un=Un.';
%%构建矩阵
A=zeros(M,N-M+1);
forn=1:
N-M+1
A(:
n)=Un(M+n-1:
-1:
n);
end
[U,S,V]=svd(A');
invphi=V*inv(S'*S)*V';
%%构建向量
P=1024;
f=linspace(-0.5,0.5,P);
omega=2*pi*f;
a=zeros(M,P);
fork=1:
P
form=1:
M
a(m,k)=exp(-1i*omega(k)*(m-1));
end
end
%%计算MVDR谱
Pmvdr=zeros(size(omega));
fork=1:
P
Pmvdr(k)=1/(a(:
k)'*invphi*a(:
k));
end
Pmvdr=abs(Pmvdr/max(abs(Pmvdr)));
Pmvdr=10*log10(Pmvdr);
kk=-0.5+(0:
P-1)*(1/(P-1));
figure
(1)
plot(kk,Pmvdr)
%%基于习题6.11的奇异值分解的MVDR方法
fork=1:
P
Sw=zeros(1,M);
fori=1:
M
Sw(i)=(a(:
k)')*V(:
i)/S(i,i);
end
P_svd(k)=1/sum((abs(Sw)).^2);
end
P_svd=abs(P_svd/max(abs(P_svd)));
P_svd=10*log10(P_svd);
xlabel('w/2*pi');ylabel('归一化频谱/dB')
title('M=4的MVDR谱')
%title('M=20的MVDR谱')
figure
(2)
plot(kk,P_svd)
xlabel('w/2*pi');ylabel('归一化频谱/dB')
title('M=4的基于SVD的MVDR频谱')
%title('M=20的基于SVD的MVDR频谱')
7.仿真题6.15
仿真结果及图形:
图17单次实验估计权值以及500次独立实验的估计权值
图18500次独立实验的学习曲线
仿真程序(6_15):
clearall
clc
%%产生AR模型的输入信号
a1=0.99;
sigma=0.995;
N=1000;
trials=500;
vn=sqrt(sigma)*randn(N,1,trials);
nume=1;
deno=[1a1];
u0=zeros(length(deno)-1,1);
xic=filtic(nume,deno,u0);
un=filter(nume,deno,vn,xic);%产生500组独立的信号
%%产生期望信号和观测数据矩阵
n0=1;
M=2;
b=un(n0+1:
N,:
:
);
L=length(b);
A=zeros(M,L,trials);
form=1:
trials
un1=[zeros(M-1,1).',un(:
:
m).'].';
fork=1:
L
A(:
k,m)=un1(M-1+k:
-1:
k);
end
end
%%RLS算法求最优权向量
delta=0.004;
lam