直角三角形等腰直角三角形斜边直线专题.docx

直角三角形等腰直角三角形斜边直线专题.docx

《直角三角形等腰直角三角形斜边直线专题.docx》由会员分享，可在线阅读，更多相关《直角三角形等腰直角三角形斜边直线专题.docx（46页珍藏版）》请在冰豆网上搜索。

直角三角形等腰直角三角形斜边直线专题

直角三角形、斜边中线、等腰直角三角形专题

一、直角三角形的性质

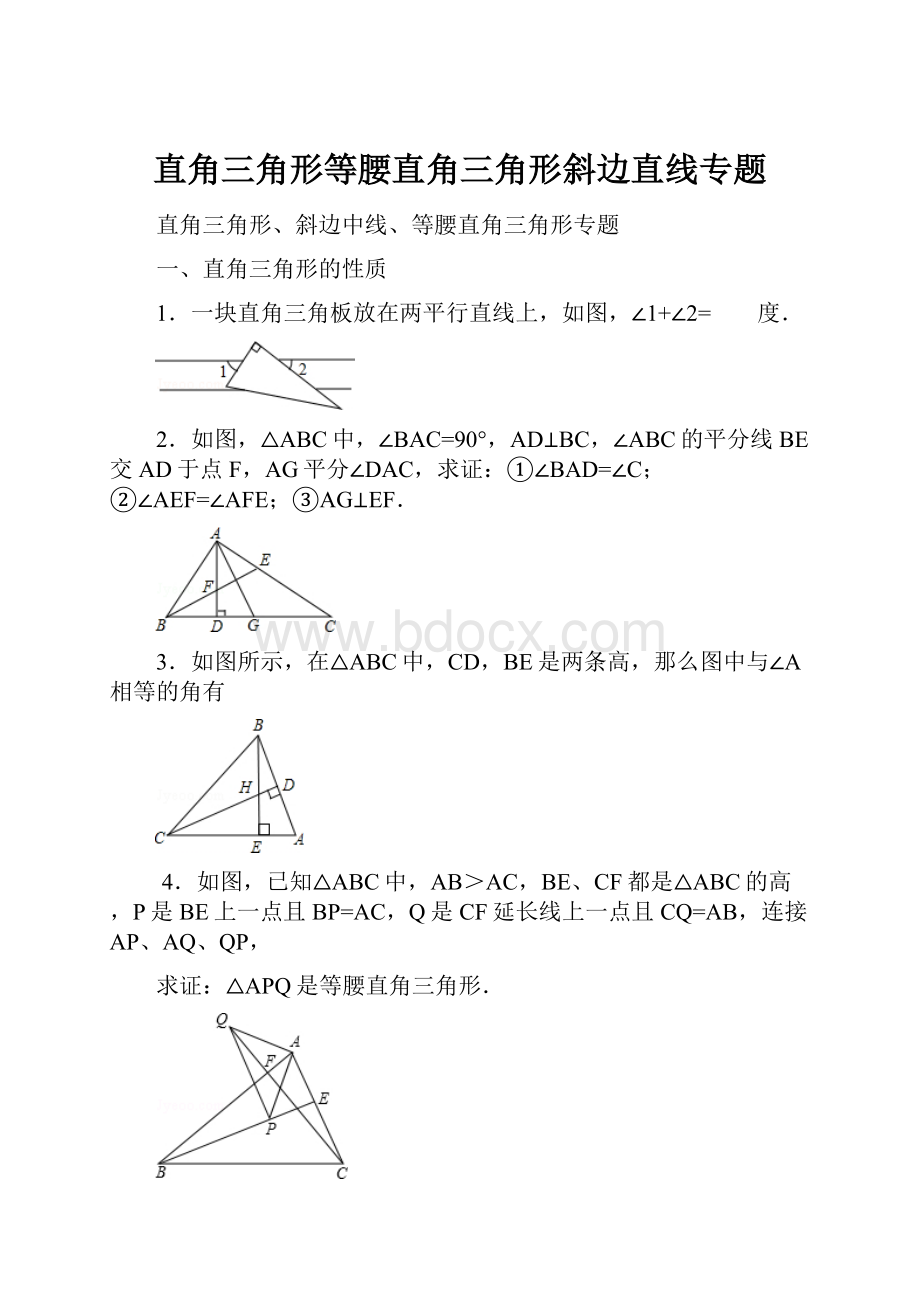
1．一块直角三角板放在两平行直线上，如图，∠1+∠2=　　度．

2．如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC，求证：

①∠BAD=∠C；②∠AEF=∠AFE；③AG⊥EF．

3．如图所示，在△ABC中，CD，BE是两条高，那么图中与∠A相等的角有

4．如图，已知△ABC中，AB＞AC，BE、CF都是△ABC的高，P是BE上一点且BP=AC，Q是CF延长线上一点且CQ=AB，连接AP、AQ、QP，

求证：

△APQ是等腰直角三角形．

二、含30°角的直角三角形的性质

5．在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，求AD的长

6．如图，∠AOP=∠BOP=15°，PC∥OA交OB于C，PD⊥OA于D，若PC=6，

求PD的长

7．如图所示，矩形ABCD中，AB=

AD，E为BC上的一点，且AE=AD，

求∠EDC的度数

8．如图，△ABC为等边三角形，点D为BC边上的中点，DF⊥AB于点F，点E在BA的延长线上，且ED=EC，若AE=2，求AF的长

9．如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，求CD的长

10．如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠BAC，DE⊥AB于E，求证：

（1）CD=DE；

（2）AC=BE；（3）BD=2CD；

三、直角三角形斜边中线问题

11．如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，求证：

△PMN为等边三角形；

12．已知锐角△ABC中，CD，BE分别是AB，AC边上的高，M是线段BC的中点，连接DM，EM．

（1）若DE=3，BC=8，求△DME的周长；

（2）若∠A=60°，求证：

∠DME=60°；

（3）若BC2=2DE2，求∠A的度数．

13．如图，在△ABC中，D是BC上一点，AB=AD，E、F分别是AC、BD的中点，EF=2，求AC的长

14．如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，求AM的最小值

15．如图，在△ABC中，∠ACB=90°，∠B=20°，D在BC上，AD=BD，E为AB的中点，AD、CE相交于点F，求∠DFE等于多少

16．如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=50°，求∠ACB′=　　．

17．如图，△ABC中，AB=AC，D为AB中点，E在AC上，且BE⊥AC，若DE=5，AE=8，求BC的长度．

18．如图，在平行四边形ABCD中，以AC为斜边作Rt△ACE，又∠BED=90°．

求证：

AC=BD．

19．已知：

如图，在Rt△ABC中，∠ACB=90°，点M是AB边的中点，CH⊥AB于点H，CD平分∠ACB．

（1）求证：

∠1=∠2．

（2）过点M作AB的垂线交CD延长线于E，求证：

CM=EM；

（3）△AEB是什么三角形？

证明你的猜想．

20．如图，已知在△ABC中，延长CA到D，使BA=BD，延长BA到E，使CA=CE，设P、M、N分别是BC、AD、AE的中点．求证：

△PMN是等腰三角形．

四、等腰直角三角形问题

21．如图，△ACB、△CDE为等腰直角三角形，∠CAB=∠CDE=90°，F为BE的中点，求证：

AF⊥DF，AF=DF．

22．已知等腰直角三角形ABC中，CD是斜边AB上的高，AE平分∠CAB交CD于E，在DB上取点F，使DF=DE，求证：

CF平分∠DCB．

23．如图，△OBD和△OCA是等腰直角三角形，∠ODB=∠OCA=90°．M是线段AB中点，连接DM、CM、CD．若C在直线OB上，试判断△CDM的形状．

24．如图①，已知点D在AC上，△ABC和△ADE都是等腰直角三角形，点M为EC的中点．

（1）求证：

△BMD为等腰直角三角形；

（2）将图①中的△ADE绕点A逆时针旋转45°，如图②所示，则

（1）题中的结论“△BMD为等腰直角三角形”是否仍然成立？

请说明理由．

25．已知：

如图△ABC中，∠A=90°，AB=AC，D是斜边BC的中点，E，F分别在线段AB，AC上，且∠EDF=90°

（1）求证：

△DEF为等腰直角三角形；

（2）求证：

S四边形AEDF=S△BDE+S△CDF；

（3）如果点E运动到AB的延长线上，F在射线CA上且保持∠EDF=90°，△DEF还仍然是等腰直角三角形吗？

请画图说明理由．

26．△ABC中，∠ABC=45°，AB≠BC，BE⊥AC于点E，AD⊥BC于点D．

（1）如图1，作∠ADB的角平分线DF交BE于点F，连接AF．求证：

∠FAB=∠FBA；

（2）如图2，连接DE，点G与点D关于直线AC对称，连接DG、EG

①依据题意补全图形；

②用等式表示线段AE、BE、DG之间的数量关系，并加以证明．

27．如图，在△ABC中，∠ACB=90°，AC=BC，D为BC中点，DE⊥AB，垂足为点E，过点B作BF∥AC交DE的延长线于点F，连接CF、AF、AD，AD与CF交于点G．

（1）求证：

△ACD≌△CBF；

（2）AD与CF的关系是　　；

（3）求证：

△ACF是等腰三角形；

（4）△ACF可能是等边三角形吗？

　　（填“可能”或“不可能”）．

直角三角形斜边中线等腰直角三角形专题

参考答案与试题解析

　1．【解答】解：

如图，∠1=∠3，∠2=∠4（对顶角相等），

∵∠3+∠4=90°，

∴∠1+∠2=90°．

故答案为：

90．

【点评】本题考查了直角三角形两锐角互余的性质，对顶角相等，熟记性质是解题的关键．

2．如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC，给出下列结论：

①∠BAD=∠C；②∠AEF=∠AFE；③∠EBC=∠C；④AG⊥EF．其中正确的结论是（　　）

A．②③④B．①③④C．①②④D．①②③

【分析】根据同角的余角相等求出∠BAD=∠C，再根据等角的余角相等可以求出∠AEF=∠AFE；根据等腰三角形三线合一的性质求出AG⊥EF．

【解答】解：

∵∠BAC=90°，AD⊥BC，

∴∠C+∠ABC=90°，

∠BAD+∠ABC=90°，

∴∠BAD=∠C，故①正确；

∵BE是∠ABC的平分线，

∴∠ABE=∠CBE，

∵∠ABE+∠AEF=90°，

∠CBE+∠BFD=90°，

∴∠AEF=∠BFD，

又∵∠AFE=∠BFD（对顶角相等），

∴∠AEF=∠AFE，故②正确；

∵∠ABE=∠CBE，

∴只有∠C=30°时∠EBC=∠C，故③错误；

∵∠AEF=∠AFE，

∴AE=AF，

∵AG平分∠DAC，

∴AG⊥EF，故④正确．

综上所述，正确的结论是①②④．

故选C．

【点评】本题考查了直角三角形的性质，等腰三角形三线合一的性质，同角的余角相等的性质以及等角的余角相等的性质，熟记各性质并准确识图理清图中各角度之间的关系是解题的关键．

3．如图所示，在△ABC中，CD，BE是两条高，那么图中与∠A相等的角的个数有（　　）

A．1个B．2个C．3个D．4个

【分析】根据已知条件CD，BE是两条高可知：

∠A+∠DCA=90°，∠ABE+∠BHD=90°，∠A+∠ABE=90°，∠CHE+∠HCE=90°，再根据同角的余角相等即可得到答案．

【解答】解：

∵CD⊥AB，

∴∠CDA=∠BDH=90°，

∴∠A+∠DCA=90°，∠ABE+∠BHD=90°，

∵BE⊥AC，

∴∠A+∠ABE=90°，∠CHE+∠HCE=90°，

∴∠A=∠BHD=∠CHE，

故选：

B．

【点评】此题主要考查了直角三角形的性质，关键是根据垂直得到有哪些角互余．

　4．如图，已知△ABC中，AB＞AC，BE、CF都是△ABC的高，P是BE上一点且BP=AC，Q是CF延长线上一点且CQ=AB，连接AP、AQ、QP，判断△APQ的形状．

【分析】利用BE、CF都是△ABC的高，求证∠1=∠2，然后求证△ACQ≌△PBA，利用AQ=AP，AQ⊥AP，即可证明△APQ是等腰直角三角形．

【解答】解：

△APQ是等腰直角三角形．

∵BE、CF都是△ABC的高，

∴∠1+∠BAE=90°，∠2+∠CAF=90°（同角（可等角）的余角相等）

∴∠1=∠2

又∵AC=BP，CQ=AB，

在△ACQ和△PBA中

，

∴△ACQ≌△PBA

∴AQ=AP，

∴∠CAQ=∠BPA=∠3+90°

∴∠QAP=∠CAQ﹣∠3=90°

∴AQ⊥AP

∴△APQ是等腰直角三角形

【点评】此题考查学生对全等三角形的判定和性质和等腰直角三角形的理解和掌握，难度不大，属于基础题．

5．（2016秋•泰山区期中）在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，则AD的长是（　　）

A．3B．4C．5D．4.5

【分析】根据直角三角形的性质求出∠A的度数，根据线段垂直平分线的性质得到DA=DC，解答即可．

【解答】解：

∵∠ACB=60°，∠B=90°，

∴∠A=30°，

∵DE是斜边AC的中垂线，

∴DA=DC，

∴∠ACD=∠A=30°，

∵BD=2，

∴AD=4，

故选B

【点评】本题考查的是线段垂直平分线的性质、直角三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

6．（2016秋•大丰市月考）如图，∠AOP=∠BOP=15°，PC∥OA交OB于C，PD⊥OA于D，若PC=6，则PD等于（　　）

A．4B．3C．2D．1

【分析】过点P作PE⊥OB于E，根据两直线平行，内错角相等可得∠AOP=∠COP，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB=30°，再根据直角三角形30°角所对的直角边等于斜边的一半解答．

【解答】解：

如图，过点P作PE⊥OB于E，

∵PC∥OA，

∴∠AOP=∠COP，

∴∠PCE=∠BOP+∠COP=∠BOP+∠AOP=∠AOB=30°，

又∵PC=6，

∴PE=

PC=3，

∵AOP=∠BOP，PD⊥OA，

∴PD=PE=3，

故选B．

【点评】本题考查了直角三角形30°角所对的直角边等于斜边的一半，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及平行线的性质，作辅助线构造出含30°的直角三角形是解题的关键．

7．（2015春•兰溪市期末）如图所示，矩形ABCD中，AB=

AD，E为BC上的一点，且AE=AD，则∠EDC的度数是（　　）

A．30°B．75°C．45°D．15°

【分析】根据矩形性质得出∠C=∠ABC=90°，AB=CD，DC∥AB，推出AE=2AB，得出∠AEB=30°=∠DAE，求出∠EDC的度数，即可求出答案．

【解答】解：

∵四边形ABCD是矩形，

∴∠C=∠ABC=90°，AB=CD，DC∥AB，

∵AB=

AD，E为BC上的一点，且AE=AD，

∴AE=2AB，

∴∠AEB=30°，

∵AD∥BC，

∴∠AEB=∠DAE=30°，

∵AE=AD，

∴∠ADE=∠AED=

（180°﹣∠EAD）=75°，

∵∠ADC=90°，

∴∠EDC=90°﹣75°=15°，

故选D．

【点评】本题考查了矩形性质，三角形的内角和定理，平行线性质，等腰三角形的性质，含30度角的直角三角形性质的应用，解此题的关键是求出∠ABC和∠EBA的度数，题目比较好，是一道综合性比较强的题目．

8．（2013春•重庆校级期末）如图，△ABC为等边三角形，点D为BC边上的中点，DF⊥AB于点F，点E在BA的延长线上，且ED=EC，若AE=2，则AF的长为（　　）

A．

B．2C．

+1D．3

【分析】过点E作EH∥AC交BC的延长线于H，证明△ABH是等边三角形，求出CH，得到BD的长，根据直角三角形的性质求出BF，计算即可．

【解答】解：

过点E作EH∥AC交BC的延长线于H，

∴∠H=∠ACB=60°，又∠B=60°，

∴△EBH是等边三角形，

∴EB=EH=BH，

∴CH=AE=2，

∵ED=EC，

∴∠EDC=∠ECD，又∠B=∠H，

∴∠BED=∠HEC，

在△BED和△HEC中，

，

∴△BED≌△HEC，

∴BD=CH=2，

∴BA=BC=4，BF=

BD=1，

∴AF=3．

故选：

D．

【点评】本题考查的是等边三角形的性质、直角三角形的性质以及等腰三角形的性质，掌握直角三角形中，30°角所对的直角边等于斜边的一半、等边三角形的三个角都是60°是解题的关键．

9．（2012春•古冶区校级期中）如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，那么CD的长是（　　）

A．2B．3C．1D．1.5

【分析】在Rt△AEC中，由于

=

，可以得到∠1=∠2=30°，又AD=BD=4，得到∠B=∠2=30°，从而求出∠ACD=90°，然后由直角三角形的性质求出CD．

【解答】解：

在Rt△AEC中，∵

=

，

∴∠1=∠2=30°，

∵AD=BD=4，

∴∠B=∠2=30°，

∴∠ACD=180°﹣30°×3=90°，

∴CD=

AD=2．

故选A．

【点评】本题利用了：

（1）直角三角形的性质；

（2）三角形内角和定理；

（3）等边对等角的性质．

10．（2012秋•包河区期末）如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠BAC，DE⊥AB于E，以下结论

（1）CD=DE；

（2）AC=BE；（3）BD=2CD；（4）DE=

AC中，正确的有（　　）

A．1个B．2个C．3个D．4个

【分析】根据角平分线的性质可得CD=DE，AC=BE，结合含30°角的直角三角形的性质可得BD=2CD，而AC和BD不一定相等，所以可得出答案．

【解答】解：

∵∠ACB=90°，∠B=30°，AD平分∠BAC，DE⊥AB，

∴DC=DE，∠ADC=∠ADE=60°，

∴AD平分∠CDE，

∴AC=AE，

在Rt△BDE中，∠B=30°，

∴BD=2DE=2CD，

在Rt△ADE中，DE=

AE=

AC，

∴正确的有

（1）、

（2）、（3），

故选C．

【点评】本题主要考查角平分线的性质及含30°角的直角三角形的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．

11．（2015秋•江阴市期中）如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：

①PM=PN；②△PMN为等边三角形；下面判断正确是（　　）

A．①正确B．②正确C．①②都正确D．①②都不正确

【分析】根据直角三角形斜边上的中线等于斜边的一半可判断①正确；根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°，再根据三角形的内角和定理求出∠BCN+∠CBM=60°，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°，从而得到∠MPN=60°，又由①得PM=PN，根据有一个角是60°的等腰三角形是等边三角形可判断②正确．

【解答】解：

①∵BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，

∴PM=

BC，PN=

BC，

∴PM=PN，正确；

②∵∠A=60°，BM⊥AC于点M，CN⊥AB于点N，

∴∠ABM=∠ACN=30°，

在△ABC中，∠BCN+∠CBM═180°﹣60°﹣30°×2=60°，

∵点P是BC的中点，BM⊥AC，CN⊥AB，

∴PM=PN=PB=PC，

∴∠BPN=2∠BCN，∠CPM=2∠CBM，

∴∠BPN+∠CPM=2（∠BCN+∠CBM）=2×60°=120°，

∴∠MPN=60°，

∴△PMN是等边三角形，正确；

所以①②都正确．

故选：

C．

【点评】本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质，等边三角形的判定与性质，熟练掌握性质是解题的关键．

　12．已知锐角△ABC中，CD，BE分别是AB，AC边上的高，M是线段BC的中点，连接DM，EM．

（1）若DE=3，BC=8，求△DME的周长；

（2）若∠A=60°，求证：

∠DME=60°；

（3）若BC2=2DE2，求∠A的度数．

【分析】

（1）根据直角三角形斜边上中线性质求出DM=

BC=4，EM=

BC=4，即可求出答案；

（2）根据三角形内角和定理求出∠ABC+∠ACB=120°，根据直角三角形斜边上中线性质求出DM=BM，EM=CM，推出∠ABC=∠BDM，∠ACB=∠CEM，根据三角形内角和定理求出即可；

（3）求出EM=

EN，解直角三角形求出∠EMD度数，根据三角形的内角和定理求出即可．

【解答】解：

（1）∵CD，BE分别是AB，AC边上的高，

∴∠BDC=∠BEC=90°，

∵M是线段BC的中点，BC=8，

∴DM=

BC=4，EM=

BC=4，

∴△DME的周长是DE+EM+DM=3+4+4=11；

（2）证明：

∵∠A=60°，

∴∠ABC+∠ACB=120°，

∵∠BDC=∠BEC=90°，M是线段BC的中点，

∴DM=BM，EM=CM，

∴∠ABC=∠BDM，∠ACB=∠CEM，

∴∠EMC+∠DMB=∠ABC+∠ACB=120°，

∴∠DME=180°﹣120°=60°；

（3）解：

过M作MN⊥DE于N，

∵DM=EM，

∴EN=DN=

DE，∠ENM=90°，

∵EM=DM=

BC，DN=EN=

DE，BC2=2DE2，

∴（2EM）2=2（2EN）2，

∴EM=

EN，

∴sin∠EMN=

=

，

∴∠EMN=45°，

同理∠DMN=45°，

∴∠DME=90°，

∴∠DMB+∠EMC=180°﹣90°=90°，

∵∠ABC=∠BDM，∠ACB=∠CEM，

∴∠ABC+∠ACB=

（180°﹣∠DMB+180°﹣∠EMC）=135°，

∴∠BAC=180°﹣（∠ABC+∠ACB）=45°．

【点评】本题考查了等腰三角形的判定和性质，三角形的内角和定理，解直角三角形的性质，直角三角形斜边上中线性质的应用，能综合运用性质进行推理是解此题的关键，本题综合性比较强，有一定的难度，注意：

直角三角形斜边上的中线等于斜边的一半．

13．（2014春•永川区校级期中）如图，在△ABC中，D是BC上一点，AB=AD，E、F分别是AC、BD的中点，EF=2，则AC的长是（　　）

A．3B．4C．5D．6

【分析】连结AF．由AB=AD，F是BD的中点，根据等腰三角形三线合一的性质得出AF⊥BD．再根据直角三角形斜边上的中线等于斜边的一半求得AC=2EF=4．

【解答】解：

如图，连结AF．

∵AB=AD，F是BD的中点，

∴AF⊥BD．

∵在Rt△ACF中，∠AFC=90°，E是AC的中点，EF=2，

∴AC=2EF=4．

故选B．

【点评】本题考查了直角三角形斜边上的中线的性质：

在直角三角形中，斜边上的中线等于斜边的一半．利用等腰三角形三线合一的性质得出AF⊥BD是解题的关键．

14．（2011秋•姜堰市期末）如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（　　）

A．2B．2.4C．2.6D．3

【分析】先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用相似三角形对应边成比例即可求得AP最短时的长，然后即可求出AM最短时的长．

【解答】解：

连结AP，在△ABC中，AB=6，AC=8，BC=10，

∴∠BAC=90°，

∵PE⊥AB，PF⊥AC，

∴四边形AFPE是矩形，

∴EF=AP．

∵M是EF的中点，

∴AM=

AP，

根据直线外一点到直线上任一点的距离，垂线段最短，

即AP⊥BC时，AP最短，同样AM也最短，

∴当AP⊥BC时，△ABP∽△CBA，

∴

=

，

∴

=

，

∴AP最短时，AP=4.8

∴当AM最短时，AM=

=2.4．

故选B．

【点评】此题主要考查学生对相似三角形判定与性质、垂线段最短和直角三角形斜边上的中线的理解和掌握，此题涉及到动点问题，有一定的拔高难度，属于中档题．

15．（2010•武隆县模拟）如图，在△ABC中，∠ACB=90°，∠B=20°，D在BC上，AD=BD，E为AB的中点，AD、CE相交于点F，∠DFE等于（　　）

A．40°B．50°C．60°D．70°

【分析】根据已知得，∠BAC=70°，∠BAD=∠B，再根据直角三角形斜边上的中线等于斜边的一半，得出∠ECB=∠B，从而得出∠ACE，再由三角形的内角和定理得∠AFC，根据对顶角相等求出答案．

【解答】解：

∵∠ACB=90°，∠B=20°，

∴∠BAC=70°，

∵AD=BD，

∴∠BAD=∠B=20°，

∴∠DAC=50°，

∵E为AB的中点，

∴BE=CE，

∴∠ECB=∠B=20°，

∴∠ACE=70°，

在△ACF中，∠ACF+∠AFC+∠FAC=180°，

∴∠AFC=60°，

∵∠DFE=∠AFC=60°（对顶角相等），

故选C．

【点评】本题考查了等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半，是基础知识要熟练掌握．

16．（2016•江岸区模拟）如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=50°，则∠ACB′=　10°　．

【分析】根据三角形内角和定理求出∠A的度数，根据直角三角形的性质分别求出∠BCD、∠DCA的度数，根据翻折变换的性质求出∠B′CD的度数，计算即可．

【解答】解：

∵∠ACB=90°，∠B=50°，

∴∠A=40°，

∵∠ACB=90°，CD是斜边上的中线，

∴CD=BD，CD=AD，

∴∠BCD=∠B=50°，∠DCA=∠A=40°，

由翻折变换的性质可知，∠B′CD=∠BCD=50°，

∴∠ACB′=∠B′CD﹣∠DCA=10°，

故答案为：

10°．

【点评】本题考查的是直角三角形的性质、翻折变换的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．

17．（2016秋•嵊州市期末）如图，△ABC中，AB=AC，D为AB中点，E在AC上，且BE⊥AC，若DE=5，AE=8，则BC的长度为　2

　．

【分析】由BE⊥AC，D为AB中点，DE=5，根据直角三角形斜边的中线等于斜边的一半，即可求得AB的长，然后由勾股定理求得BC的长．

【解答】解：

∵BE⊥AC，

∴∠AEB=90°，

∵D为AB中点，

∴AB=2DE=2×5=10，

∵AE=8，

∴BE=

=6．

∴BC=

=

=2

，

故