fluent考试题4九月整理doc.docx

fluent考试题4九月整理doc.docx

《fluent考试题4九月整理doc.docx》由会员分享，可在线阅读，更多相关《fluent考试题4九月整理doc.docx（12页珍藏版）》请在冰豆网上搜索。

fluent考试题4九月整理doc

问题描述

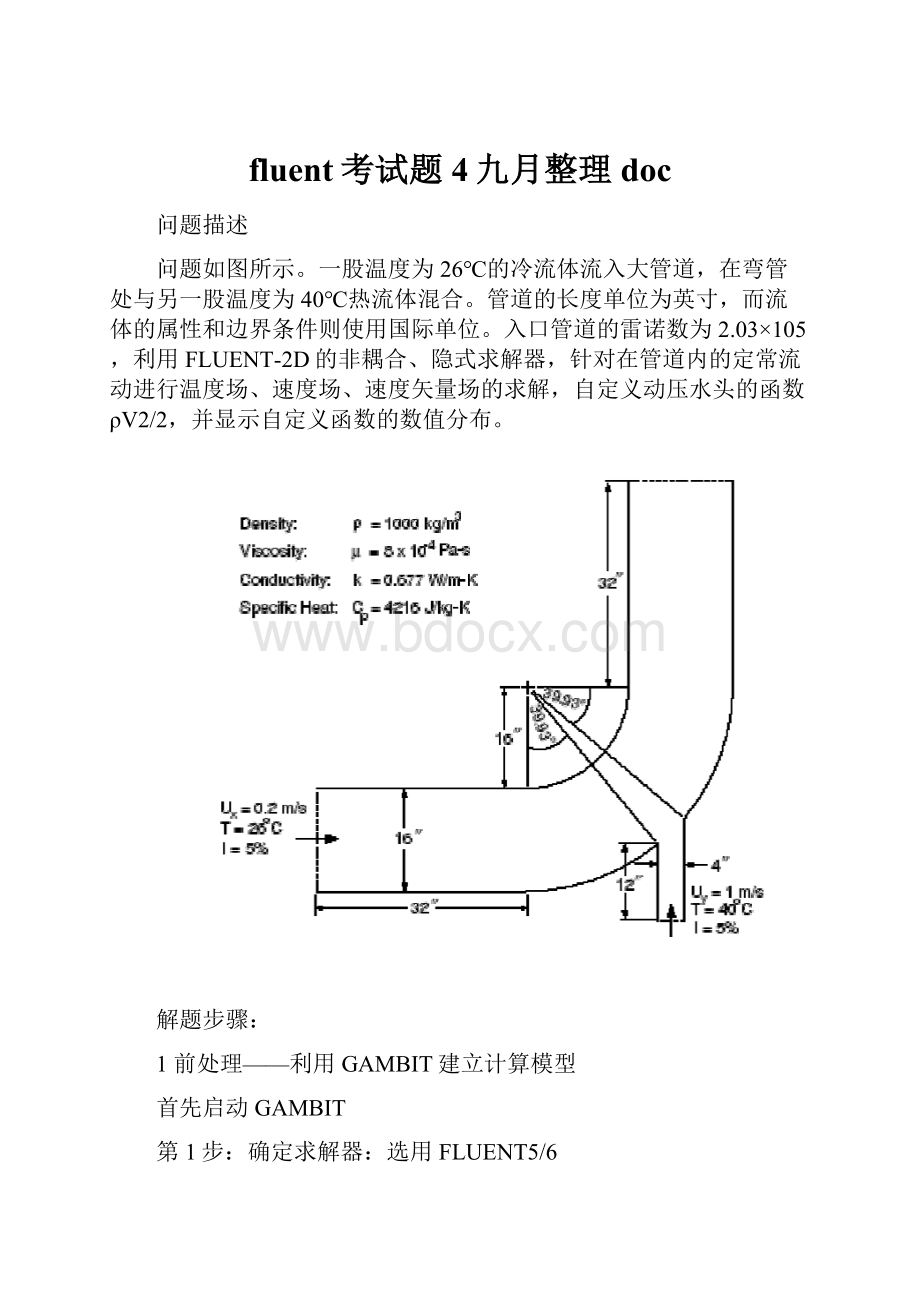
问题如图所示。

一股温度为26℃的冷流体流入大管道，在弯管处与另一股温度为40℃热流体混合。

管道的长度单位为英寸，而流体的属性和边界条件则使用国际单位。

入口管道的雷诺数为2.03×105，利用FLUENT-2D的非耦合、隐式求解器，针对在管道内的定常流动进行温度场、速度场、速度矢量场的求解，自定义动压水头的函数ρV2/2，并显示自定义函数的数值分布。

解题步骤：

1前处理——利用GAMBIT建立计算模型

首先启动GAMBIT

第1步：

确定求解器：

选用FLUENT5/6

第2部：

创建坐标图：

operation—vertexcommandbutton—global

在global中依次输入坐标（0,0）（32,0）（0,16）（32,16）（48,32）（48,64）（64,32）（64,64）

确定小管嘴的坐标：

利用copyverticesbutton键，先输入y=-12确定一个点，在copy这个点，输入x=4确定小管嘴的另一个点。

第3步：

由节点创建直线：

由作业要求连接节点做出直线。

第4步：

创建圆弧边

利用operation—edgecommandbutton—arc确定两条圆弧分别用vertices：

center、end-points和vertices：

radius、startangle、endangle

在小管嘴侧的圆弧的angle分别输入startangle=270endangle=309.93和startangle=320.07endangle=360由此可确定圆弧。

第5步：

有线组成面：

operation—facecommandbutton依次用shift+鼠标左键，顺序点击线来创建面，组成面的边为蓝色。

第6步：

确定边界线的内部节点分布并创建结构化网格：

mesh—edge键中选择intervalcount来输入每个边需要的节点数。

保证对边节点数一样。

利用mesh—face—meshfaces显示网格，然后在关闭网格。

第7步：

设置边界类型：

输入inlet1，type为velocity；输入inlet2，type为velocity；输入outlet，type为outflow。

其他的边默认为墙体wall。

第8步：

输出网格并保存会话：

file—export—mesh，关闭GAMBIT。

2利用fluent进行混合器内流动与换热的仿真计算

启动fluent的2D求解器后进行以下操作。

第1步：

与网格的相关操作：

1.1读入网格mesh文件

1.2网格检查grid—check信息

1.3平滑（和交换）网格

点击grid—smooth/swap，默认设置。

1.4确定长度的单位：

在gridwasgreatedin中选择in

1.5显示网格如下：

图1管道网格图

第2步建立求解模型

2.1保持solver默认不变

2.2设置标准

湍流模型：

选择k-epsilon，然后保留默认设置

2.3选择能量方程define—model—energyequation

第3步：

设置流体的物理特性

3.1创建新流体，取名为water，在属性栏内输入流体的物理特性：

density=1000，Cp=4216,

Thermalconductivity=0.667,viscosity=0.0008

第4步：

设置边界条件

4.1设置流体：

在zone栏内选择fluid，在type栏选fluid，点击set键后在material下选water

4.2设置冷水入口速度边界条件

设置inlet1，输入velocityspecificationmethod选择components所以X—velocity=0.2Y—velocity=0，temperature=299，turbulenceintensity=5%

设置inlet2，输入velocityspecificationmethod选择components所以X—velocity=0Y—velocity=1，temperature=313，turbulenceintensity=5%

设置outlet，保留默认设置

设置wall,保留默认设置

第5步：

求解

5.1流场初始化：

在computefrom中选择inlet1

5.2在计算时绘制残差曲线图solve—monitor—residual

5.4开始进行100次迭代计算，得到残差曲线图如下：

图2迭代计算40次后所得的残差曲线图

5.5点击report—fluexs检查流入和流出整个系统的质量，动量，能量是

否守恒。

第6步：

显示计算结果

6.1利用不同颜色显示速度分布图如下：

图3初次计算得出的速度分布图

6.2显示温度场图如下：

图4初次计算得出的温度分布图

6.3显示速度矢量场图如下：

图5速度矢量图

6.4显示流场中的等压线图如下：

图6管道内的等压线图

6.5创建出流口截面上的温度XY曲线图如下：

图7出流口截面上的温度分布图

6.6制作出流口截面上的压力分布图如下：

图8出流口截面上的压力分布图

6.7制作出流口截面上的速度分布图如下：

图9出流口截面上的速度分布图

6.8自定义函数ρV2/2

6.9显示自定义函数的数值分布图如下：

图10管道内速度水头等值线图

第7步：

用二阶离散化方法重新计算

7.1打开求解控制器设置对话框，设置能量方程的二阶离散，降低松弛系数

Solve—controls—solution中，在discretization下energy项，选择secondorderupwind；在under-relaxationfactors项的energy项，填入0.8

7.2继续进行100次迭代计算，如下图：

图11使用二阶离散化方法计算得到的残差曲线图

7.3温度分布图如下：

图12使用二阶离散化方法计算得到的管道内的温度分布图

第8步自适应性网格修改功能

8.1显示基于单元的温度分布图如下：

图13基于单元的温度分布图

8.2绘制用于改进网格的温度梯度图如下：

图14管道内的温度梯度

8.3在一定范围内绘制温度梯度，标出改进的单元

在options项不选择autorange；在min栏输入0.01

图15温度梯度较高的单元

8.4对高温度梯度区域内的网格进行改进图如下：

图16需进行网格细化的单元标示图

8.5显示改进后的网格图如下：

图17改进后的网格图

8.6继续进行100次迭代计算得残差曲线图如下：

图18全部迭代计算的残差值曲线

8.7查看温度分布情况图如下：

图19充填方式显示的温度分布图

图20等值线方式显示的温度分布图

8.8查看速度分布

图21使用改进网格计算的速度分布

8.9查看速度矢量场

图22使用改进网格计算的速度矢量场

结论：

在计算过程中，我使用了三种离散方法：

1.最初的网格，能量方程采用一阶离散方法。

2.最初的网格，能量方程采用二阶离散方法。

3.利用温度梯度定位网格单元并给予改进，能量方程采用二阶离散方法。

将三种方法得出的温度分布图进行比较，可以明显看出数值计算结果的发散性越来越小。

在FLUENT中，默认的是一阶离散方法，其计算结果可以作为高阶离散方法的初始值。