通信综合课程设计.doc

通信综合课程设计.doc

《通信综合课程设计.doc》由会员分享，可在线阅读，更多相关《通信综合课程设计.doc（37页珍藏版）》请在冰豆网上搜索。

武汉理工大学《通信系统课群综合训练与设计》课程设计说明书

课程设计任务书

学生姓名：

专业班级：

通信0905

指导教师：

工作单位：

信息工程学院

题目:

通信系统课群综合训练与设计

初始条件：

1.MATLAB软件2．PC机

要求完成的主要任务:

（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）

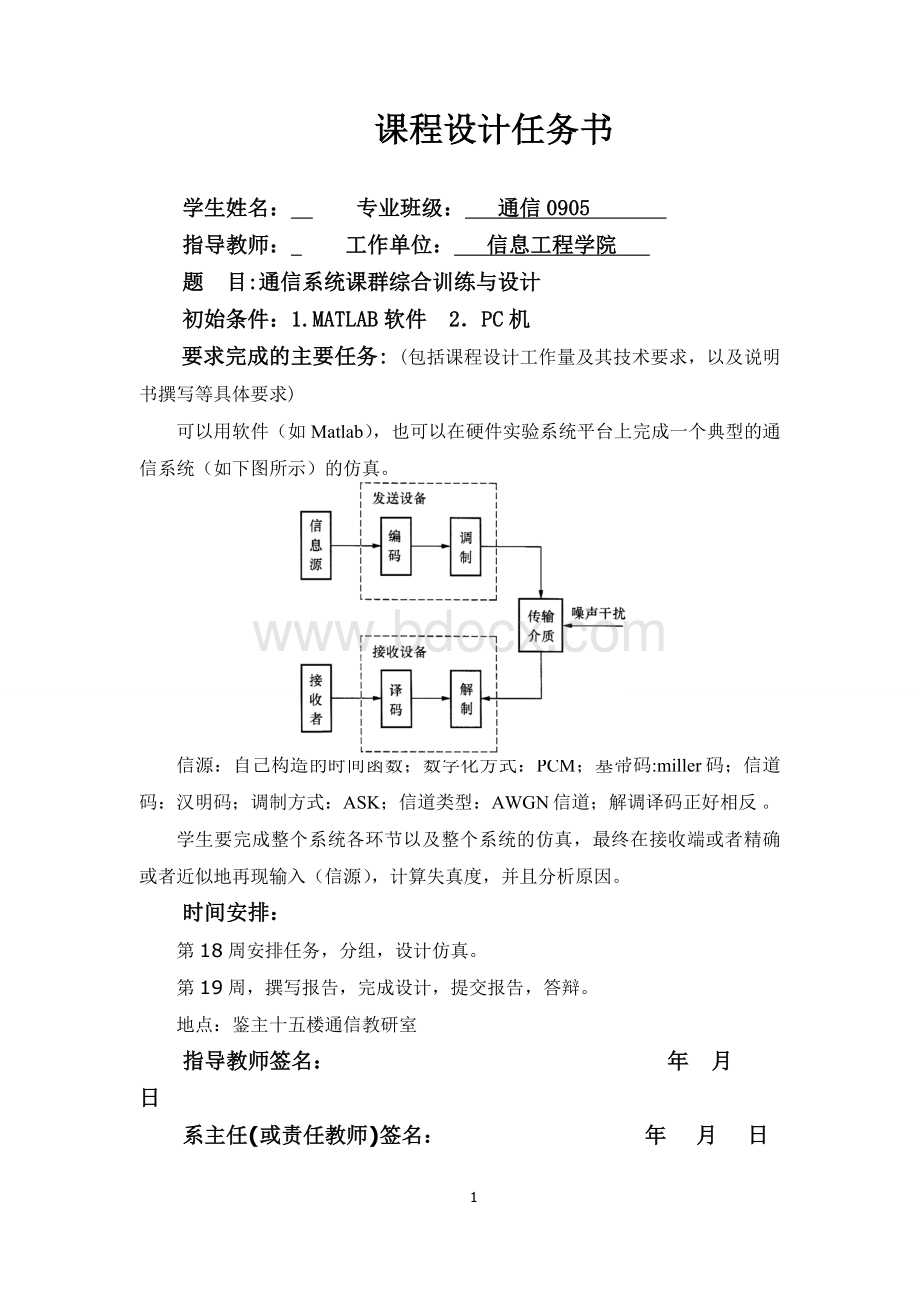
可以用软件（如Matlab），也可以在硬件实验系统平台上完成一个典型的通信系统（如下图所示）的仿真。

信源：

自己构造的时间函数；数字化方式：

PCM；基带码:

miller码；信道码：

汉明码；调制方式：

ASK；信道类型：

AWGN信道；解调译码正好相反。

学生要完成整个系统各环节以及整个系统的仿真，最终在接收端或者精确或者近似地再现输入（信源），计算失真度，并且分析原因。

时间安排：

第18周安排任务，分组，设计仿真。

第19周，撰写报告，完成设计，提交报告，答辩。

地点：

鉴主十五楼通信教研室

指导教师签名：

年月日

系主任（或责任教师）签名：

年月日

目录

摘要 I

ABSTRACT II

通信系统课群综合训练与设计 1

1设计任务及要求 1

2设计原理 1

2.1通信系统组成 1

2.2数字化方式：

PCM基本原理 2

2.2.1抽样 2

2.2.2量化 3

2.2.3编码 5

2.3基带码：

miller码 6

2.4信道码：

汉明码 6

2.3.1汉明码编码原理 6

2.3.2汉明码纠错原理 8

2.3.3汉明码matlab函数介绍 9

2.4调制方式：

2ASK 9

2.4.12ASK调制 9

2.4.22ASK解调 10

2.5信道类型：

AGWN信道 11

3仿真结果 11

3.1原始信号 11

3.2PCM编码仿真 12

3.3MIller编码仿真 13

3.4Hamming编码信号 13

3.5ASK调制信号 14

3.6信号AWGN处理 14

3.7ASK解调信号 15

3.8Hanmming解码信号 15

3.9Miller解码信号 16

3.10PCM解码信号 16

4总结 17

5参考文献 18

附录 19

32

摘要

在数字通信系统中，需要将输入的数字序列映射为信号波形在信道中传输，此时信源输出数字序列，经过信号映射后成为适于信道传输的数字调制信号，并在接收端对应进行解调恢复出原始信号。

所以本论文主要研究了数字信号的传输的基本概念及数字信号传输的传输过程和如何用MATLAB软件仿真设计数字传输系统。

首先介绍了本课题的理论依据，包括数字通信，数字基带传输系统的组成及数字信号的传输过程。

然后按照仿真过程基本步骤用MATLAB的仿真工具实现了数字基带传输系统的仿真过程，对系统进行了分析。

关键词：

PCM、Miller码、汉明码、ASK、AWGN

ABSTRACT

Indigitalcommunicationsystem,needtheinputdigitalsequencemapforsignaltransmissioninthechannel,thesourceoutputdigitalsequence,aftersignalaftermappingbecomesuitableforchanneltransmissionofdigitalmodulationsignals,andatthereceivingendcorrespondingtoresumetheoriginalsignaldemodulation.SothisthesismainlystudiesthedigitalsignaltransmissionofthebasicconceptandthedigitalsignaltransmissiontransmissionprocessandhowtouseMATLABsimulationsoftwaretodesigndigitaltransmissionsystem.Thefirstinterfaceintroducedthistopictheoreticalbasis,includingdigitalcommunication,digitalbasebandtransmissionsystemcompositionanddigitalsignaltransmissionprocess.AccordingtothesimulationprocessandbasicstepsoftheMATLABsimulationtoolstoimplementthedigitalbasebandtransmissionsystem'sprocess,thesystemisanalyzed.

Keywords:

PCM、Miller-code、Hamming-code、ASKmodulation、AWGN

通信系统课群综合训练与设计

1设计任务及要求

（1）按下列要求对一个通信系统进行仿真

表1-1

模拟信源（模拟话音）

数字化方式

基带码

信道码

调制方式

信道

解调

信道解码

基带解码

数模转换

自己构造一时间函数

PCM

miller码

汉明码

ASK

AWGN

与发送端对应

（2）学生要完成整个系统各环节以及整个系统的仿真，最终在接收端或者精确或者近似地再现输入（信源），计算失真度，并且分析原因。

2设计原理

2.1通信系统组成

通信的目的是传输信息。

通信系统的作用就是将信息从信息源发送到一个或多个目的地。

对于任何一个通信系统，均可视为由发送端、信道和接收端三大部分组成（如图2-1所示）。

接收设备

发送设备

信息源

编码设备

信道

信息源

噪声源

发送端

接收端

信道

调制设备

译码码设备

解调设备

图2-1

2.2数字化方式：

PCM基本原理

脉冲编码调制（PCM）简称脉码调制，它是一种用二进制数字代码来代替连续信号的抽样值，从而实现通信的方式。

由于这种通信方式抗干扰能力强，因此在光钎通信、数字微波通信、卫星通信中均获得了极为广泛的运用。

PCM信号的形成是模拟信号经过“抽样、量化、编码”三个步骤实现的。

分别完成时间上离散、幅度上离散、及量化信号的二进制表示。

根据CCITT的建议，为改善小信号量化性能，采用压扩非均匀量化，有两种建议方式，分别为A律和μ律方式，我国采用了A律方式，由于A律压缩实现复杂，常使用13折线法编码。

2.2.1抽样

所谓抽样，就是对模拟信号进行周期性扫描，把时间上连续的信号变成时间上离散的信号。

该模拟信号经过抽样后还应当包含原信号中所有信息，也就是说能无失真的恢复原模拟信号。

它的抽样速率的下限是由抽样定理确定的。

在一个频带限制在（0，fh）内的时间连续信号f（t），如果以1/2fh的时间间隔对它进行抽样，那么根据这些抽样值就能完全恢复原信号。

或者说，如果一个连续信号f（t）的频谱中最高频率不超过fh，当抽样频率fS≥2fh时，抽样后的信号就包含原连续的全部信息。

这就是抽样定理。

2.2.2量化

从数学上来看，量化就是把一个连续幅度值的无限数集合映射成一个离散幅度值的有限数集合。

如图3.1所示量化器Q输出L个量化值，k=1，2，3，…，L。

常称为重建电平或量化电平。

当量化器输入信号幅度落在与之间时，量化器输出电平为。

这个量化过程可以表达为：

（1）

这里称为分层电平或判决阈值。

通常称为量化间隔。

量化后的抽样信号于量化前的抽样信号相比较，当然有所失真，且不再是模拟信号。

这种失真在接收端还原模拟信号是变现为噪声，并称为量化噪声。

量化噪声的大小取决于把样值分级“取整”的方式，分的级数越多，即量化极差或间隔越小，量化噪声也越小。

模拟信号的量化分为均匀量化和非均匀量化。

由于均匀量化存在的主要缺点是：

无论抽样值大小如何，量化噪声的均方根值都固定不变。

因此，当信号较小时，则信号量化噪声功率比也就很小，这样的话化信噪比就难以达到给定的要求。

通常，把满足信噪比要求的输入信号取值范围定义为动态范围，可见，对于弱信号时，均匀量化时的信号动态范围将受到较大的限制。

为了克服这个缺点，实际中，往往采用非均匀量化。

非均匀量化是根据信号的不同区间来确定量化间隔的。

对于信号取值小的区间，其量化间隔也小；反之，量化间隔就大。

它与均匀量化相比，有两个突出的优点。

首先，当输入量化器的信号具有非均匀分布的概率密度（实际中常常是这样）时，非均匀量化器的输出端可以得到较高的平均信号量化噪声功率比；其次，非均匀量化时，量化噪声功率的均方根值基本上与信号抽样值成比例。

因此量化噪声对大、小信号的影响大致相同，即改善了小信号时的量化信噪比。

实际中，非均匀量化的实际方法通常是将抽样值通过压缩再进行均匀量化。

通常使用的压缩器中，大多采用对数式压缩。

广泛采用的两种对数压缩律是压缩律和A压缩律。

美国采用压缩律，我国和欧洲各国均采用A压缩律，因此，PCM编码方式采用的也是A压缩律。

所谓A压缩律也就是压缩器具有如下特性的压缩律：

A律：

（2）

式中，x为归一化输入，y为归一化输出，A、μ为压缩系数。

A律压扩特性是连续曲线，A值不同压扩特性亦不同，在电路上实现这样的函数规律是相当复杂的。

实际中，往往都采用近似于A律函数规律的13折线（A=87.6）的压扩特性。

这样，它基本上保持了连续压扩特性曲线的优点，又便于用电路实现，本设计中所用到的PCM编码正是采用这种压扩特性来进行编码的。

实际中A律常采用13折线近似如图2-2所示

图2-2A律13折线

其具体分法如下:

先将X轴的区间[0，1]一分为二，其中点为1/2,取区间[1/2,1]作为第八段;

区间[0,1/2]再一分为二，其中点为1/4,取区间[1/4,1/2]作为第七段;

区间[0,1/4]再一分为二，其中点为1/8,取区间[1/8,1/4]作为第六段;

区间[0,1/8]一分为二，中点为1/16,取区间[1/16,1/8]作为第五段;

图2-2

区间[0,1/16]一分为二，中点为1/32,取区间[1/32,1/16]作为第四段;

区间[0,1/32]一分为二，中点为1/64,取区间[1/64,1/32]作为第三段;

区间[0,1/64]一分为二，中点为1/128,区间[1/128,1/64]作为第二段;

区间[0,1/128]作为第一段。

然后将