北师大版八年级数学上册第1章勾股定理培优试题.docx
《北师大版八年级数学上册第1章勾股定理培优试题.docx》由会员分享,可在线阅读,更多相关《北师大版八年级数学上册第1章勾股定理培优试题.docx(10页珍藏版)》请在冰豆网上搜索。
北师大版八年级数学上册第1章勾股定理培优试题
第一章勾股定理
1.1探索勾股定理专题一有关勾股定理的折叠问题
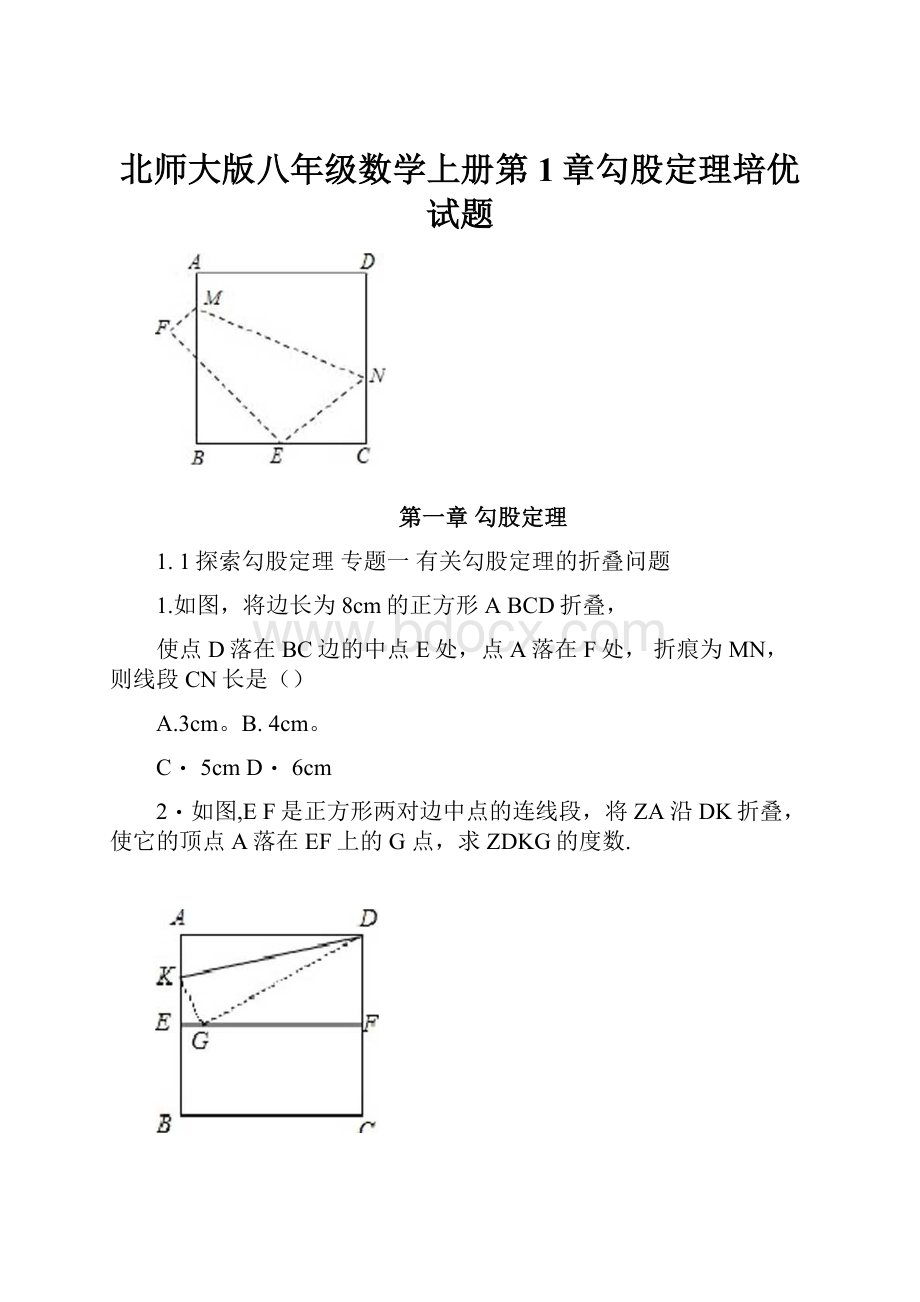
1.如图,将边长为8cm的正方形ABCD折叠,
使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是()
A.3cm。
B.4cm。
C・5cmD・6cm
2・如图,EF是正方形两对边中点的连线段,将ZA沿DK折叠,使它的顶点A落在EF上的G点,求ZDKG的度数.
3.已知RtAABC中,ZACB二90°,CA二CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.13)如图①,当AM二BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将ABCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,APyX的形状是・线段AM、BN.M
N之间的数量关系是;上
(2)如图②,当扇形C
EF绕点C在ZACB内部旋转时,线段MN、AM、BN之间的数量关系是
—.试证明你的猜想:
(3)当扇形CEF绕点C旋转至图③的位宜时,线段MN、AM、BN之间的数疑关系是—■(不要求证明)
专题二勾股定理的证明
4•在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用四个完全相同的宜角三角形拼图的方式验证了勾股左理的正确性.
问题1:
以直角三角形的三边为边向外作等边三角形,探究S'+S〃与S的关系(如图1)・问题2:
以直角三角形的三边为斜边向外作等腰宜角三角形,探究S'+S"与S的关系(如图2)・
问题3:
以直角三角形的三边为直径向外作半圆,探究S'+S”与S的关系(如图3)・
5.如图,是用硬纸板做成的两种直角三角形各有若干个,图①中两直角边长分别为a和
b,斜边长为C:
图②中两宜角边长为C.请你动脑,将它们拼成能够证明勾股泄理的图形.
(1)请你画出一种图形,并验证勾股定理.
(2)你非常聪明,能再拼岀另外一种能证明勾股定理的图形吗?
请画出拼后的图形(无需证明).
①
答案:
1・A【解析】设CN=xcm,则DN=(8-x)cm.由折叠的性质知EN=DN=(8-x)cm,
而FC=LbC=4cm,在RtAECN中,由勾股左理可知E^EC^CN2.RP(8-x)2=162
+/,丄整理得16x=4&所以x=3.故选A.
2•解:
•:
DF='cD=、DG,:
•乙DGF二30°・TZEKG+二90。
乙KGE+乙DGF=22
90°严•••ZfKG=ZDGF二30°・\92ZDKG+ZGKE=180°,:
•乙DKMM・
3•解:
(1)根据折叠的性质知:
△CAM^ZkCPM,HCNB竺HCNP・:
.AM=PM,ZA=Z
CPWPN=NB—CPN・:
.乙MPN=ZA+ZB=9$.PM=PN=AM=BNa故厶PMN是
等腰直角三角形,AM?
+BN2=MN2(或AM=BN=^MN).
2
(2)W+BA—MN?
.
证明:
如图,将Zk/ICM沿CM折叠,得厶DCM,连DN,则AAGW^ADCM.:
.CD=CA,DM=AM.ZDCM=ZACM.同理可知ZDCN=ZBCN,\DCN9\BCN、DN=BN,而ZMDC=ZA=45°,ZCDAr=ZB=45°,AZMDN=90f:
.D
DgMg故A^+B^MN2・a(3)AM2+BN2=M1^\
解法同
(2)・
4・解:
探究1:
由等边三角形的性质知:
S'二亘凡S—迺*测S'+
444
S"二色W+S)・因为s+tf^c2.所以S'+S"=S.礫究2:
由等腰直角三角
4
形的性质知片扑T厂S十,则.因为心,所以
S*S”=S・
探究3:
由圆的面积计算公式知:
S=Lnc\
888
则S+S"=4(/+b2),因为a2+b2=c\所以S'+S”=S・
8
5.解:
(1)如图所示,
根据正方形的而积可得(a+b)2=4X1ab+2
即a2+b2=c2・
(2)如图所示小
1.2一定是直角三角形吗
专题判断三角形形状
1.已知a,b,c为ZkABC的三边,且满足a:
c:
-bc2=a-b,则它的形状为()
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
2.aAABC中,a=m3+n%b=m2-n\c=2mn,且m>n>0,1(a)你能判断ZkABC的最长边吗?
请说明理由:
(2)AABC是什么三角形,请通过计算的方法说明.
3.张老师在一次“探究性学AT课中,设计了如下数表:
n
2
3
4
5
•••
a
22-l
3:
-l
42-l
5:
-l
•••
b
4
6
8
10
•••
c
22+l
3:
+1
4=+l
5=+l
•••
答案:
1・D【解析】Vac"~b"c"=a1~b\必.I(ac--b"c")-(a1-b)=0,c"(a+b)(a—b)-(a+b)(a—b)(a:
+b:
)=0»
/.(a+b)(a—b)(ca-b:
)二0,
Va+b^0,aAa-b二0或c2-a3-bs=0t所以a=b或cs=a°+b2,即它是等腰三角形或直角三角形.
故选D.
2•解:
(1)a是最长边,其理由是:
aTa-b=(m"+n2)—(m--n-)=2n">0,^a~c=(m"+n2)-2mn=(m-n)2>0,
•\a>b,a>Ct/.a是最长边.
(2)AABC是直角三角形,其理由是>Vb5+c3=(m3-n2)2+(2mn)3=(m3+n3)5=a3,如:
△ABC是直角三角形.
3・解:
⑴由图表可以得岀工•••n=2时,a=22-1,b=2X2,c=2?
+l;
n二3时,a=3:
-l,b=2X3,c=32+l;^n=4时,a=4-1fb=2X4fc=42+l.
・・.a二1,b二2n,c=£+l』
(2)以a、b、c为边的三角形是直角三角形.
Va2+b3=(n2-l)3+4n2=ni+2n2+1,叱2=(ns+l)2=n4+2n3+1,
/.a3+b2=c>.•-以a.b、c为边的三角形是直角三角形・
1・3勾股定理的应用
专題最短路径的探究
1.编制一个底而周长为a、高为b的圆柱形花柱架,需用沿圆柱
表而绕织一周的竹条若干根,如图中的A’CiBi,A:
CoB2,则每一根这样的竹条的长度最少是.
2.请阅读下列材料:
问题:
如图
(1),一圆柱的底而半径和高均为5dm,BC是底而
直径,求一只蚂蚁从A点出发沿圆柱表而爬行到点C的最短路线.
小明设计了两条路线:
路线1:
侧而展开图中的线段AC.如下图
(2)所示:
设路线1的长度为厶,则=AC2=AB2+BC1=52+(5d=25+25n2:
路线2:
高线AB+底而直径BC,如上图
(1)所示,
设路线2的长度为人,
则F=(AB+BC)2=(5+10)2=225.
•・・/「_//=25+25疋_225=25冗2_200=25(疋_8)>0・U)
O
所以要选择路线2较短。
(1)小明对上述结论有些疑惑,于是他把条件改成:
“圆柱的底而半径为1dm,髙AB为5dnT继续按前而的方式进行讣算.
请你帮小明完成下而的讣算:
路线]:
牢=AC1=;
路线2:
/22=(AB+BC)2=,
V62/22,・•・/,/2(填>或<).
所以应选择路线(填1或2)较短.
(2)请你帮小明继续研究:
在一般情况下,当圆柱的底而半径为r,髙为h时,应如何选
择上而的两条路线才能使蚂蚁从点A出发沿圆柱表而爬行到C点的路线最短.
3.探究活动:
有一圆柱形食品盒,它的髙等于8cm,底而直径为一cm,蚂蚁爬行的速度为
2cm/s.
(1)如果在盒内下底而的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?
(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)
(2)如果在盒外下底而的A处有一只蚂蚁,它想吃到盒内对而中部点B处的食物,那么它至少需要多少时间?
(盒的厚度和蚂蚁的大小忽略不计)
答案:
1.>]a2+h2【解析】底而周长为a、高为b的圆柱的侧而展开图为矩形,它的边长分别为a,b,所以对角线长为J/+,,所以每一根这样的竹条的长度最少是(/+/.
2•解:
(1)25+/49<<1
(2)1i:
=AC:
=AB?
4-BC==h:
+(nr)\
1/=(AB+BC)2=(h+2r)\^1(nr)-(h+2r)2=r(n2r-4r-4h)=r[(n
2-4)r-4h].4/>
r恒大于0,只需看后而的式子即可小当r=—一时,1?
=132;
7T一4
Alj
当d-时,1/>1二
矿一4
4/1
当r<^4—时,1"1/・
矿-4
1Q
3・解:
⑴如图,AC=n-—4-2=9cm,BC=4cm,则蚂蚁走过的最短路径为:
7t
S・
AB二JB+42二Qcm,所以妍三2二孚(s),即至少需要乎
(2)如图,作B关于EF的对称点D,连接AD,交EF于点P,连接BP,贝I」
蚂蚁泄的最短路程是AP+PB二AD,由图可知,AC二9cm,CD二8+4=12(cm)」所以
AD=>/92+122=15(cm),15^-2=7.5(s)