数值分析第二次程序题.docx
《数值分析第二次程序题.docx》由会员分享,可在线阅读,更多相关《数值分析第二次程序题.docx(18页珍藏版)》请在冰豆网上搜索。
数值分析第二次程序题
数值分析第二次程序题——插值法
1.对Runge函数
在区间[-1,1]作下列插值逼近,并和R(x)的图像进行比较,并对结果进行分析。
(1)以
为节点,Newton插值
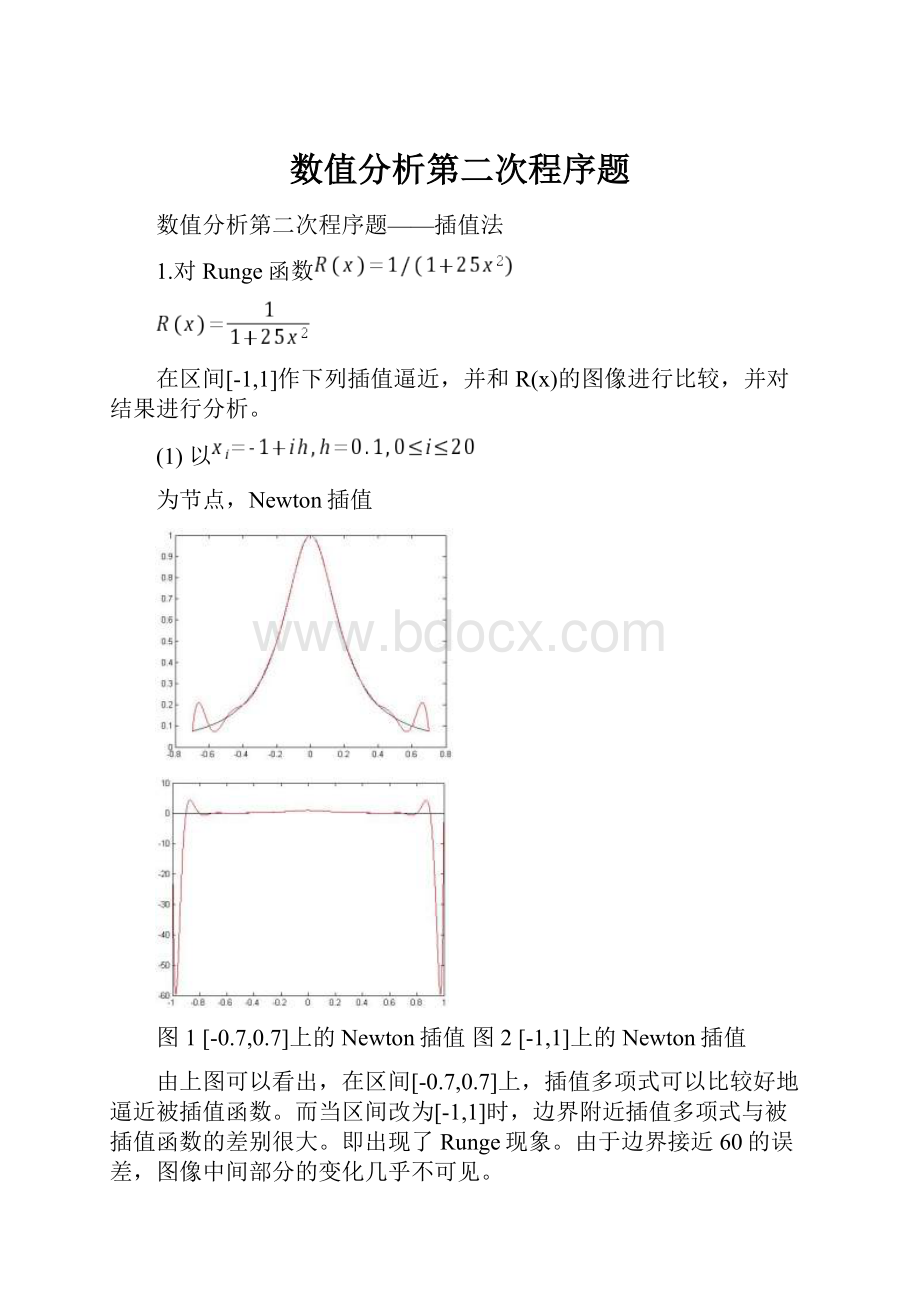
图1[-0.7,0.7]上的Newton插值图2[-1,1]上的Newton插值
由上图可以看出,在区间[-0.7,0.7]上,插值多项式可以比较好地逼近被插值函数。
而当区间改为[-1,1]时,边界附近插值多项式与被插值函数的差别很大。
即出现了Runge现象。
由于边界接近60的误差,图像中间部分的变化几乎不可见。
主要原因是被插值函数的任意阶导数不能达到一致有界。
其插值余项
不趋近零。
插值多项式不能收敛到被插值函数。
牛顿差值函数
functionf=niudun(z,N,n)
f=N(1,1);
x=-1:
0.1:
1;
fork=2:
n
a=1;
forr=1:
(k-1)
a=a*(z-x(r));
end
f=f+N(k,k)*a;
end
主程序
x=-1:
0.1:
1;
n=length(x);
fori=1:
n
y(i)=1/(1+25*x(i)*x(i));
end
N=zeros(n,n);
N(:
1)=y';
forj=2:
n
fork=j:
n
N(k,j)=(N(k,j-1)-N(k-1,j-1))/(x(k)-x(k-j+1));
end
end
fort=1:
n
c(t)=N(t,t);
end
z=-1:
0.001:
1;
m=size(z,2);
fori=1:
m
Runge(i)=1/(1+25*z(i)*z(i));
f(i)=niudun(z(i),N,n);
end
plot(z,Runge,'k',z,f,'r')
(2)以
为节点,Lagrange插值
图3以Chebyshev多项式零点为插值点图4以等距节点为插值点
如图所示,使用Chebyshev多项式零点构造的Lagrange插值多项式比较接近原函数,没有出现Runge现象,图4为第一小问中的等距节点插值,可以明显的看出以Chebyshev多项式零点为插值点的优势。
主要原因是其多项式误差为
,在区间内一致收敛。
Lagrange函数
functionlag=lagrange(z,x,y)
fori=1:
21
l(i)=1;
forj=1:
21
ifj~=i
l(i)=l(i)*(z-x(j))/(x(i)-x(j));
end
end
end
l=l';
lag=y*l;
主程序
fori=1:
21
x(22-i)=cos((2*i-1)*pi/42);
end
fori=1:
21
y(i)=1/(1+25*x(i)*x(i));
end
z=-1:
0.001:
1;
m=length(z);
fori=1:
m
f(i)=1/(1+25*z(i)*z(i));
lag(i)=lagrange(z(i),x,y);
end
plot(z,f,'k',z,lag,'r')
(3)以
为节点,分段线性插值
如下图所示,分段线性插值多项式比较接近原函数,没有出现Runge现象。
但是可以明显地看到在区间[-0.1,0.1]中,线性插值的拟合度较低,因为这一部分的函数的曲率较大,也就是二阶导数较大。
由误差估计公式
可知这一部分的误差较大。
图5线性插值
(4)以
为节点,三次自然样条插值
图6三次自然样条插值函数图像
由上图可以看出,三次样条插值函数的曲线及其光滑,图中并没有将插值函数连起来,否则基本无法分辨出原函数和插值函数的图像,说明得到的函数十分接近被插值函数。
另外,题目要求自然样条插值,也就是再两端的二阶导数为0,需在变成过程中加以注意。
x=-1:
0.1:
1;
n=length(x);
fori=1:
n
y(i)=1/(1+25*x(i)*x(i));
end
fori=1:
n-1
h(i)=x(i+1)-x(i);
end
fori=1:
n-2
u(i)=h(i)/(h(i+1)+h(i));
r(i)=1-u(i);
end
G=zeros(n-2,n-2);
fori=1:
n-2
G(i,i)=2;
end
fori=2:
n-2
G(i,i-1)=u(i-1);
G(i,i+1)=r(i-1);
end
d=zeros(1,n-2);
fori=1:
n-2
d(i)=6*((y(i+2)-y(i+1))/h(i+1)-(y(i+1)-y(i))/h(i))/(h(i+1)+h(i));
end
d=d';
M=G\d;
M=[0;M;0];
fori=1:
n-1
z=[x(i):
0.01:
x(i+1)];
m=length(z);
forj=1:
m
s(j)=M(i)*(x(i+1)-z(j))^3/0.6+M(i+1)*(z(j)-x(i))^3/0.6+(y(i)-M(i)*0.01/6)*(x(i+1)-z(j))/0.1+(y(i+1)-M(i+1)*0.01/6)*(z(j)-x(i))/0.1;
end
plot(z,s,'*r','MarkerSize',3)
holdon
end
holdon
z=-1:
0.01:
1;
fori=1:
201
f(i)=1/(1+25*z(i)*z(i));
end
plot(z,f,'b')
2.对函数:
在区间[-1,1]作下列插值逼近,并和被插值函数的图像进行比较,并对结果进行分析。
(1)以
为节点,Newton插值
首先对函数进行简要分析,函数f(x)是分段函数,并且在x=0处不连续,对于插值计算,只需要函数值,所以除了函数作图和计算函数值有所不同以外,程序的主体部分没有明显改动,所以将本题程序统一放在最后。
本小题中
图7[-1,1]上的Newton插值图8[-0.7,0.7]上的Newton插值
由上图可以看出,在区间[-0.7,0.7]上,插值多项式可以已经无法较好地逼近被插值函数了,而当区间改为[-1,1]时,边界附近插值多项式与被插值函数的差别迅速扩大。
即出现了Runge现象。
由于边界接近1000的误差,图像中间部分的变化几乎不可见。
相比于第一题Runge现象更为明显。
主要原因是被插值函数不连续,导致其插值余项
可能无穷大。
插值多项式不能收敛到被插值函数。
(2)以
为节点,Lagrange插值
图9以Chebyshev多项式零点为插值点
如图所示,使用Chebyshev多项式零点构造的Lagrange插值多项式比较接近原函数,没有出现Runge现象,并且可以看出,在不连续点位置插值效果一般,但是在函数两端的拟合效果明显要好,说明使用Chebyshev多项式零点构造的Lagrange插值多项式在连续函数上的应用效果更佳。
(3)以
为节点,分段线性插值
图1021个插值点线性插值图11201个插值点线性插值
如下图所示,分段线性插值多项式比较接近原函数,没有出现Runge现象。
此例中我们看到了线性插值的强大优势,当原函数较为光滑,曲率较小,即使是分段函数对线性插值的影响也极为有限,当插值点个数扩大10倍达到201个时,可以明显的看出线性插值的优势所在。
(4)以
为节点,三次自然样条插值
图12三次自然样条插值函数图像
由上图可以看出,三次样条插值函数的曲线及其光滑,但是与其他多项式拟合一样在不连续点处存在较大的误差,但是与第一二小问中的Lagrange插值多项式相比,三次样条插值可以更快的脱离不连续点的影响,并在其他位置上表现出很好的拟合效果。
综合以上2题我们可以初步得出这样的结论:
当函数连续光滑,使用Chebyshev多项式零点构造的Lagrange插值多项式可以有效地避免Runge现象,但三次样条插值函数的曲线更为优秀。
但是当函数出现不连续点时,分段线性插值的优势明显,可以在不连续段处达到很好的拟合效果,并且可以迅速脱离不连续点的影响,所以在做函数插值时在斜率很大的部分可以考虑使用分段线性插值,其他部分采用三次样条效果最好。
牛顿插值
x=-1:
0.1:
1;
n=length(x);
fori=1:
10
y(i)=sin(pi*x(i));
end
fori=11:
15
y(i)=cos(pi*x(i));
end
fori=15:
n
y(i)=0;
end
N=zeros(n,n);
N(:
1)=y';
forj=2:
n
fork=j:
n
N(k,j)=(N(k,j-1)-N(k-1,j-1))/(x(k)-x(k-j+1));
end
end
fort=1:
n
c(t)=N(t,t);
end
z=-0.1:
0.01:
0.1;
m=length(z);
fori=1:
m
nd(i)=niudun(z(i),N,n);
end
v=linspace(-1,0,100);
u=sin(pi*v);
plot(v,u,'k')
holdon
v=linspace(0,0.5,50);
u=cos(pi*v);
plot(v,u,'k')
holdon
v=linspace(0.5,1,50);
u=0;
plot(v,u,'k')
holdon
plot(z,nd,'r')
以Chebyshev多项式零点为插值点
fori=1:
21
x(22-i)=cos((2*i-1)*pi/42);
end
fori=1:
21
ifx(i)<0
y(i)=sin(pi*x(i));
elseifx(i)>0.5
y(i)=0;
else
y(i)=cos(pi*x(i));
end
end
z=-1:
0.001:
1;
m=length(z);
fori=1:
m
lag(i)=lagrange(z(i),x,y);
end
v=linspace(-1,0,100);
u=sin(pi*v);
plot(v,u,'k')
holdon
v=linspace(0,0.5,50);
u=cos(pi*v);
plot(v,u,'k')
holdon
v=linspace(0.5,1,50);
u=0;
plot(v,u,'k')
holdon
plot(z,lag,'r')
线性插值
x=-1:
0.01:
1;
fori=1:
201
ifx(i)<0
y(i)=sin(pi*x(i));
elseifx(i)>0.5
y(i)=0;
else
y(i)=cos(pi*x(i));
end
end
z=-1:
0.001:
1;
n=length(z);
m=floor((z+1)/0.01)+1;
fori=1:
n-1
l(i)=y(m(i))+(y(m(i)+1)-y(m(i)))/(x(m(i)+1)-x(m(i)))*(z(i)-x(m(i)));
end
l(2001)=y(201);
f(2001)=y(201);
v=linspace(-1,0,100);
u=sin(pi*v);
plot(v,u,'k')
holdon
v=linspace(0,0.5,50);
u=cos(pi*v);
plot(v,u,'k')
holdon
v=linspace(0.5,1,50);
u=0;
plot(v,u,'k')
holdon
plot(z,l,'r')
三次样条插值
x=-1:
0.1:
1;
n=length(x);
fori=1:
21
ifx(i)<0
y(i)=sin(pi*x(i));
elseifx(i)>0.5
y(i)=0;
else
y(i)=cos(pi*x(i));
end
end
fori=1:
n-1
h(i)=x(i+1)-x(i);
end
fori=1:
n-2
u(i)=h(i)/(h(i+1)+h(i));
r(i)=1-u(i);
end
G=zeros(n-2,n-2);
fori=1:
n-2
G(i,i)=2;
end
fori=2:
n-2
G(i,i-1)=u(i-1);
G(i,i+1)=r(i-1);
end
d=zeros(1,n-2);
fori=1:
n-2
d(i)=6*((y(i+2)-y(i+1))/h(i+1)-(y(i+1)-y(i))/h(i))/(h(i+1)+h(i));
end
d=d';
M=G\d;
M=[0;M;0];
fori=1:
n-1
z=[x(i):
0.01:
x(i+1)];
m=length(z);
forj=1:
m
s(j)=M(i)*(x(i+1)-z(j))^3/0.6+M(i+1)*(z(j)-x(i))^3/0.6+(y(i)-M(i)*0.01/6)*(x(i+1)-z(j))/0.1+(y(i+1)-M(i+1)*0.01/6)*(z(j)-x(i))/0.1;
end
plot(z,s,'*r','MarkerSize',3)
holdon
end
v=linspace(-1,0,100);
u=sin(pi*v);
plot(v,u,'k')
holdon
v=linspace(0,0.5,50);
u=cos(pi*v);
plot(v,u,'k')
holdon
v=linspace(0.5,1,50);
u=0;
plot(v,u,'k')
holdon