六年级数学北师大版下册全册同步练习题Word文档下载推荐.docx
《六年级数学北师大版下册全册同步练习题Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《六年级数学北师大版下册全册同步练习题Word文档下载推荐.docx(79页珍藏版)》请在冰豆网上搜索。
四、选一选。
(把正确答案的序号填入括号内)
(1)求一个圆柱形水桶能盛多少水,就是求水桶的()
A.侧面积B.表面积C.容积D.体积
(2)把一个棱长是6cm的正方体木块削成一个最大的圆柱,圆柱的体积是()cm3。
A.75.36B169.56C.301.44D.678.24
(3)一个圆柱,如果它的底面直径扩大为2倍,高不变,那么它的体积扩大为()倍。
A.2B.4C.6D.8
五、根据已知条件求下面圆柱的体积。
(1)底面直径是
,高是底面直径的
倍。
(2)底面周长是31.4cm,高是2.5m。
六、生活问题我解决。
做一个圆柱形鱼缸,底面半径是3dm,高是5dm。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(得数保留整十平方分米)
(2)这个鱼缸能装水多少千克?
(1L水重1kg)
圆锥
(1)圆锥的底面是个(),侧面是一个()。
(2)从圆锥的()到()的距离是圆锥的高。
(3)圆锥有()条高。
三、择优录取。
(1)以下面各图形的一条边为轴,旋转一周,能形成圆锥的图形是()
(2)
左图是一个圆柱和一个圆锥,从不同方向会看到不同的图形,从右面看到的图形是()
四、请标出圆锥的各部分名称。
五、填表。
名称
底面半径
底面直径
底面周长
底面积
6dm
4cm
31.4m
六、有一个底面直径为20cm的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口3cm。
若将一个圆锥形铅锤浸入杯中,水会溢出20ml。
求铅锤的体积。
六年级数学北师大版圆柱和圆锥的练习课同步练习
一、单选题
1.等底等高的圆柱、正方体、长方体的体积相比较()
A.正方体体积大 B.长方体体积大
C.圆柱体体积大 D.一样大
2.圆柱体的体积和等底面积的圆锥体的体积相等,圆柱体的高是圆锥体的()
A.3倍B.2倍C.
D.
3.24个铁圆锥,可以熔铸成等底等高的圆柱体的个数是:
A.12个 B.8个 C.36个 D.72个
4.圆柱体的底面半径和高都扩大3倍,它的体积扩大的倍数是:
A.3 B.6 C.9 D.27
二、填空题
1.用一张边长是20厘米的正方形铁皮,围成一个圆柱体,这个圆柱体的侧面积是( ).
2. 直圆柱的底面周长6.28分米,高1分米,它的侧面积是( )平方分米,体积是( )立方分米.
3.一个圆柱体的底面直径和高都是0.6米,它的体积是( )立方分米.
4.一个圆锥体和它的等底等高的圆柱体的体积相差12立方厘米,圆锥体的体积是(
)立方厘米.
5.一个圆柱形铅块,可以熔铸成( )个和它等底等高的圆锥形零件.
6.做一个圆柱体,侧面积是9.42平方厘米,高是3厘米,它的底面半径是( )厘米.
7.一个圆锥体体积是2立方米,高是4分米,底面积是( ).
8.一个圆柱体和一个圆锥体的体积与高都相等,圆柱的底面积是18平方厘米,圆锥的底面积是( )平方厘米.
9.一个圆柱体和一个圆锥体的底面积和高都相等.已知圆锥体的体积是7.8立方米,那么圆柱体的体积是( )立方米.
10.一个圆锥的体积是76立方米,底面积是19平方米,这个圆锥的高是( )米.
11.把一个高6厘米的圆柱体削成最大圆锥体,这个圆锥的体积是9.42立方厘米,它的底面积是( )厘米.
三、应用题
1.求空心圆柱体体积.(单位:
厘米)
2.一个圆锥形砂堆,底面周长是31.4米,高3米,每方砂重1.8吨,用一辆载重4.5吨的汽车,几次可以运完?
(得数保留整数)
3.如图,这顶帽子,帽顶部分是圆柱形,用花布做的,帽沿部分是一个圆环,也是用同样花布做,已知帽顶的半径,高和帽沿宽都是1分米,那么做这顶帽子至少要用多少平方分米的花布?
【试题答案】
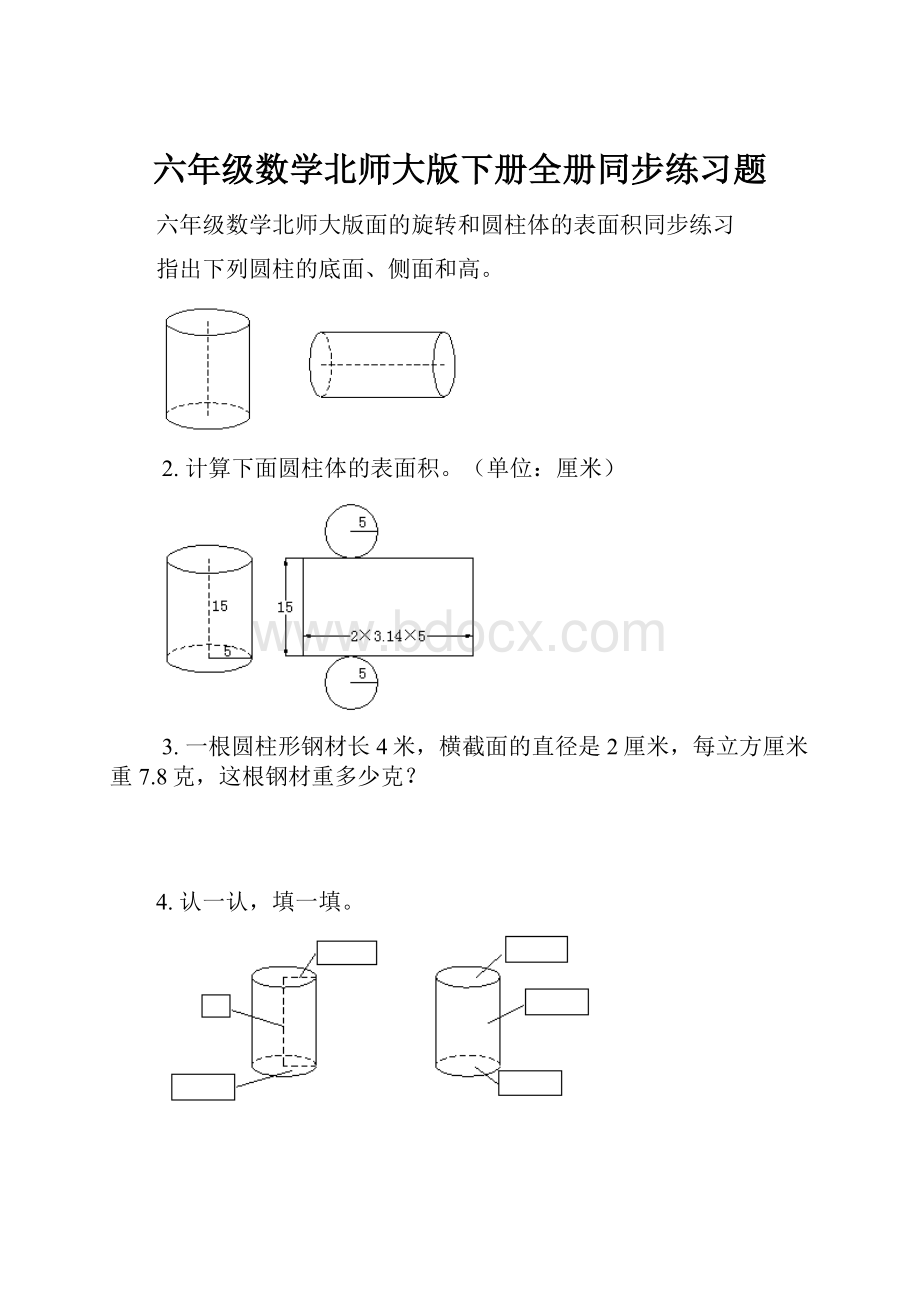
1.指出下列圆柱的底面、侧面和高。
解:
(1)侧面积:
(2)底面积:
(3)表面积:
答:
圆柱体的表面积是628平方厘米。
(1)底面半径:
(2)圆柱体积:
(3)钢材的重量:
这根钢材重9796.8克。
4.认一认,填一填。
5.把对应的部分用线连一连。
6.按照图意剪一剪。
7.仔细观察,研究圆柱和圆锥的关系。
(2)
28.26cm2
12cm
339.12cm3
(8)
113.04cm3
(4)
706.5cm2
20cm
14130cm3
(6)
4710cm3
(3)
78.5cm2
1570cm3
(5)
cm3
c.上面8个图形中还有哪几个图形需要单独计算体积,请算一下。
六年级数学北师大版圆柱的体积和圆锥的体积同步练习参考答案
一、5.5
27.812
120
631
二、
(1)753.6
(2)2.5(3)2
三、
(1)×
(2)×
(3)×
(4)×
(5)×
四、
(1)C
(2)B(3)B
五、
(1)
六、
(1)
一、5276400.64
10303.89
二、
(1)圆曲面
(2)顶点底面圆心(3)一
三、
(1)C
(2)B
四、
五、
3dm
18.84dm
28.26dm2
8cm
25.12cm
50.24cm2
5m
10m
78.5m2
六、
解析:
铅锤的体积等于底面直径为20cm、高为3cm的圆柱的体积加上溢出杯外的水的体积,与铅锤的形状无关。
六年级数学北师大版正比例和反比例同步练习
1.甲、乙、丙三种糖果每千克售价分别是22元、30元、33元.某人买这三种糖果,在每种糖果上所花钱数一样多,问他买的这些糖果每千克的平均价是多少元?
2.一个分数,分子与分母之和是100.如果分子加23,分母加32,新的分数约分后是
,原来的分数是多少?
3.加工一个零件,甲需3分钟,乙需3.5分钟,丙需4分钟,现有1825个零件要加工,为尽早完成任务,甲、乙、丙应各加工多少个?
所需时间是多少?
4.某团体有100名会员,男会员与女会员的人数之比是14∶11,会员分成三个组,甲组人数与乙、丙两组人数之和一样多.各组男会员与女会员人数之比是:
甲:
12∶13,乙:
5∶3,丙:
2∶1,
那么丙组有多少名男会员?
5.一段路程分成上坡、平路、下坡三段,各段路程长之比依次是1∶2∶3.小龙走各段路程所用时间之比依次是4∶5∶6.已知他上坡时速度为每小时3千米,路程全长50千米.问小龙走完全程用了多少时间?
一、
1.D2.D3.B4.D
二、
1.400平方厘米2.6.28;
3.143.0.054
4.6
5.36.0.57.500平方分米8.549.23.4
10.1211.4.71
三、
1.182
立方厘米
2.32次
3.18.84平方分米
4.4厘米
1.解一:
设每种糖果所花钱数为1,因此平均价是
答:
这些糖果每千克的平均价是27.5元.
上面解法中,算式很容易列出,但计算却使人感到不易.最好的计算方法是,用22,30,33的最小公倍数330,乘这个繁分数的分子与分母,就有:
事实上,有稍简捷的解题思路.
解二:
先求出这三种糖果所买数量之比.
不妨设,所花钱数是330,立即可求出,
所买数量之比是甲∶乙∶丙=15∶11∶10.
平均数是(15+11+10)÷
3=12.
单价33元的可买10份,要买12份,单价是
下面我们转向求比的另一问题,即“比的分配”问题,当一个数量被分成若干个数量,如果知道这些数量之比,我们就能求出这些数量.
2.解:
新的分数,分子与分母之和是(10+23+32),而分子与分母之比2∶3.因此
3.解:
三人同时加工,并且同一时间完成任务,所用时间最少,要同时完成,应根据工作效率之比,按比例分配工作量.
三人工作效率之比是
他们分别需要完成的工作量是
所需时间是:
700×
3=2100分钟=35小时.
甲、乙、丙分别完成700个,600个,525个零件,需要35小时.
这是三个数量按比例分配的典型例题.
4.解:
甲组的人数是100÷
2=50(人).
乙、丙两组男会员人数是56-24=32(人).
丙组有12名男会员.
上面解题的最后一段,实质上与“鸡兔同笼”解法一致,可以设想,“兔的脚数”是
,
5.解一:
通常我们要求出小龙走平路与下坡的速度,先求出走各段路程的速度比.
上坡、平路、下坡的速度之比是
走完全程所用时间
小龙走完全程用了10小时25分.
上面是通常思路下解题.1∶2∶3计算中用了两次,似乎重复计算,最后算式也颇费事.事实上,灵活运用比例有简捷解法.
全程长是上坡这一段长的(1+2+3)=6(倍).如果上坡用的时间是4份,全
设小龙走完全程用x小时.可列出比例式
x:
=(4+5+6):
24
六年级数学北师大版反比例和观察与探究同步练习
25分钟)
1.甲、乙两同学的分数比是5∶4.如果甲少得22.5分,乙多得22.5分,则他们的分数比是5∶7.甲、乙原来各得多少分?
2.张家与李家的收入钱数之比是8∶5,开支的钱数之比是8∶3,结果张家结余240元,李家结余270元.问每家各收入多少元?
3.A和B两个数的比是8∶5,每一数都减少34后,A是B的2倍,求这两个数.
4.小明和小强原有的图画纸之比是4∶3,小明又买来15张.小强用掉了8张,现有的图画纸之比是5∶2.问原来两人各有多少张图画纸?
5.粗蜡烛和细蜡烛长短一样.粗蜡烛可以点5小时,细蜡烛可以点4小时.同时点燃这两支蜡烛,点了一段时间后,粗蜡烛长是细蜡烛长的2倍.问这两支蜡烛点了多少时间?
6.箱子里有红、白两种玻璃球,红球数是白球数的3倍多2只.每次从箱子里取出7只白球,15只红球,经过若干次后,箱子里剩下3只白球,53只红球,那么,箱子里原来红球数比白球数多多少只?
甲、乙两人的分数之和没有变化.原来要分成5+4=9份,变化后要分成5+7=12份.如何把这两种分法统一起来?
这是解题的关键.9与12的最小公倍数是36,我们让变化前后都按36份来算.
5∶4=(5×
4)∶(4×
4)=20∶16.
5∶7=(5×
3)∶(7×
3)=15∶21.
甲少得22.5分,乙多得22.5分,相当于20-15=5份.因此原来
甲得22.5÷
5×
20=90(分),
乙得22.5÷
16=72(分).
原来甲得90分,乙得72分.
我们再介绍一种能解本节所有问题的解法,也就是通过比例式来列方程.
设原先甲的得分是5x,那么乙的得分是4x.根据得分变化,可列出比例式.
(5x-22.5)∶(4x+22.5)=5∶7
即5(4x+22.5)=7(5x-22.5)
15x=12×
22.5
x=18.
2.解一:
我们采用“假设”方法求解.
如果他们开支的钱数之比也是8∶5,那么结余的钱数之比也应是8∶5.张家结余240元,李家应结余x元.有
240∶x=8∶5,x=150(元).
实际上李家结余270元,比150元多120元.这就是8∶5中5份与8∶3中3份的差,每份是120÷
(5-3)=60.(元).因此可求出
张家收入720元,李家收入450元.
设张家收入是8份,李家收入是5份.张家开支的3倍与李家开支的8倍的钱一样多.
我们画出一个示意图:
张家开支的3倍是(8份-240)×
3.
李家开支的8倍是(5份-270)×
8.
从图上可以看出
5×
8-8×
3=16份,相当于
270×
8-240×
3=1440(元).
因此每份是1440÷
16=90(元).
张家收入是90×
8=720(元),李家收入是90×
5=450(元).
本题也可以列出比例式:
(8x-240)∶(5x-270)=8∶3.
然后求出x.事实上,解方程求x的计算,与解二中图解所示是同一回事,图解有算术味道,而且一些数量关系也直观些.
减少相同的数34,因此未减时,与减了以后,A与B两数之差并没有变,解题时要充分利用这一点.
8∶5,就是8份与5份,两者相差3份.减去34后,A是B的2倍,就是2∶1,两者相差1.将前项与后项都乘以3,即2∶1=6∶3,使两者也相差3份.现在就知道34是8-6=2(份)或5-3=2(份).因此,每份是34∶2=17.
A数是17×
8=136,B数是17×
5=85.
A,B两数分别是136与85.
本题也可以用“假设”方法求解,不过要把减少后的2∶1,改写成8∶4.解一:
充分利用已知数据的特殊性.
4.解:
4+3=7,5+2=7,15-8=7.原来总数分成7份,变化后总数仍分成7份,总数多了7张,因此,
新的1份=原来1份+1
原来4份,新的5份,5-4=1,因此
新的1份有15-1×
4=11(张).
小明原有图画纸11×
5-15=40(张),
小强原有图画纸11×
2+8=30(张).
原来小明有40张,小强有30张图画纸.
我们也可采用“假设”方法.先要将两个比中的前项化成同一个数(实际上就是通分)
4∶3=20∶15
5∶2=20∶8.
但现在是20∶8,因此这个比的每一份是
当然,也可以采用实质上与解方程完全相同的图解法.
解三:
设原来小明有4“份”,小强有3“份”图画纸.
把小明现有的图画纸张数乘2,小强现有的图画纸张数乘5,所得到的两个结果相等.我们可以画出如下示意图:
从图上可以看出,3×
5-4×
2=7(份)相当于图画纸15×
2+8×
5=70(张).
因此每份是10张,原来小明有40张,小强有30张.
这几道题是同一类型的问题.用比例式的方程求解没有多大差别.用算术方法,却可以充分利用已知数据的特殊性,找到较简捷的解法,也启示一些随机应变的解题思路.另外,解方程的代数运算,对小学生说来是超前的,不容易熟练掌握.第2题的解一,也是一种通用的方法.“假设”这一思路是很有用的,希望读者能很好掌握,灵活运用.从课外的角度,我们更应启发小同学善于思考,去找灵巧的解法,这就要充分利用数据的特殊性.因此我们总是先讲述灵巧的解法,利于心算,促进思维.
5.
我们把问题改变一下:
设细蜡烛长度是2,每小时点去
,问过多长时间两支蜡烛长度相等.
现在两者相关是(2-1),每小时能缩小差距
,因此两者相等需要时间是(2-1)÷
(小时)
这两支蜡烛点了3小时20分.
把细蜡烛的长度和每小时烧掉的长度都乘以2,使原来要考虑的“2倍”变成“相等”,思考就简捷了.解这类问题这是常用的技巧.
6.解:
因为红球是白球的3倍多2只,每次取15只,最后剩下53只,所以对3倍的白球,每次取15只,最后应剩51只.
因为白球每次取7只,最后剩下3只,所以对3倍的白球,每次取7×
3=21只,最后应剩3×
3=9只.因此.共取了(51-3×
3)÷
(7×
3-15)=7(次).
红球有15×
7+53=158(只).
白球有7×
7+3=52(只).
原来红球比白球多158-52=106(只).
箱子里原有红球数比白球数多106只.
六年级数学北师大版正反比例综合复习同步练习
40分钟)
1.某工厂有职工1800人,男女职工人数比是5∶4,求男女职工各多少人?
2.沙子灰是灰和沙子混合而成的,它们的比是7∶3.要用280吨沙子灰,则灰和沙子各需多少吨?
3.图书馆买来180本儿童故事书,按1∶2∶3分给低、中、高年级同学阅读.低、中、高年级各分到多少本?
4.学校把560棵的植树任务,按照五年级三个班人数分配给各班.一班47人,二班45人,三班48人.三个班级各植树多少棵?
5.有一块试验田,周长200米,长与宽的比是3∶2.这块试验田的面积是多少平方米?
6.看图编一道按比例分配题解答.
7.某商品76件,出售给33位顾客,每位顾客最多买三件,买1件按定价,买2件降价10%,买3件降价20%.最后结算,平均每件恰好按原定价的85%出售,那么买3件的顾客有多少人?
8.有两堆棋子,A堆有黑子350个和白子500个,B堆有黑子400个和白子100个.为了使A堆中黑子占A堆的
,B堆中黑子占
.要从B堆中拿到A堆黑子、白子各多少个?
9.高中学生的人数是初中学生人数的
,高中毕业生的人数是初中毕业生人数的
,高、初中毕业生毕业后,高、初中留下的人数都是520人,问高、初中毕业生共有多少人?
10.张、王、李三个人共有108元,张用了自己钱数的
,王用了自己钱数的
,李用了自己钱数的
,各买了一支相同的钢笔,问张和李剩下的钱共有多少元?
1.男女职工各1000人和800人
2.灰和沙子各需196吨和84吨
3.低、中、高年级各分到30本,60本,90本.
4.提示:
①三个班植树的总棵树是几?
②题目要求按什么比?
人数比是几比几?
③三个数的和及三个数的比知道后,根据“按比例分配”的规律,一班188棵,二班180棵,三班192棵
5.提示:
(这道题给了长与宽的比是3∶2,指的是一个长与一个宽的比,而周长包括2个长和2个宽,因此先求出一个长宽的和,即200÷
2,然后把100按3∶2去分配.)
这块试验田的面积是2400平方米
6.苹果和桔子共重1200千克,糨们的重量比是3:
1,求苹果和桔子各重多少千克?
苹果和桔子各重900千克和300千克
7.解:
题目已给出平均数85%,可作比较的基准.
1人买3件少5%×
3;
1人买2件多5%×
2;
1人买1件多15%×
1.
1人买3件与1人买1件成A组,即按1∶1比例,2人买3件与3人买2件成B组,即按2∶3的比例.
A组是2人买4件,每人平均买2件.
B组是5人买12件,每人平均买2.4件.
现在已建立了一个鸡兔同笼型问题:
总脚数76,总头数33,兔脚数2.4,鸡脚数2.
B组人数是
(76-2×
33)÷
(24-2)=25(人),
其中买3件
(人),
买2件
A组人数是33-25=8(人),其中买3件4人,买1件4人.
10+4=14(人).
买3件的顾客有14位.
8.解:
要B堆中黑子占
,即黑子与白子之比是3:
1.先从B堆中拿出黑子100个,使余下黑子与白子之比是(40-100)∶100=3∶1.再要从B堆拿出黑子与白子到A堆,拿出的黑子与白子数目也要保持3
∶1的比.
现在A堆已有黑子350+100=450个,与已有白子500个,相差50个.要黑子占
,就是两种棋子一样多.
从B堆再拿出黑子与白子,要相差50个,又要符合3∶1这个比,要拿出白子数是
50÷
(3-1)=25(个).
再要拿出黑子数是25×
3=75(个).
从B堆拿出黑子175个,白子25个.
由于时间的关系这些题放在模拟试题中,让学生自己阅读理解
9.解一:
先画出如下示意图:
6-5=1,相当于图中相差17-12=5(份),初中总人数是5×
6=30份,因此