北大心理统计知识点总结统计Word文档下载推荐.docx

北大心理统计知识点总结统计Word文档下载推荐.docx

《北大心理统计知识点总结统计Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《北大心理统计知识点总结统计Word文档下载推荐.docx（34页珍藏版）》请在冰豆网上搜索。

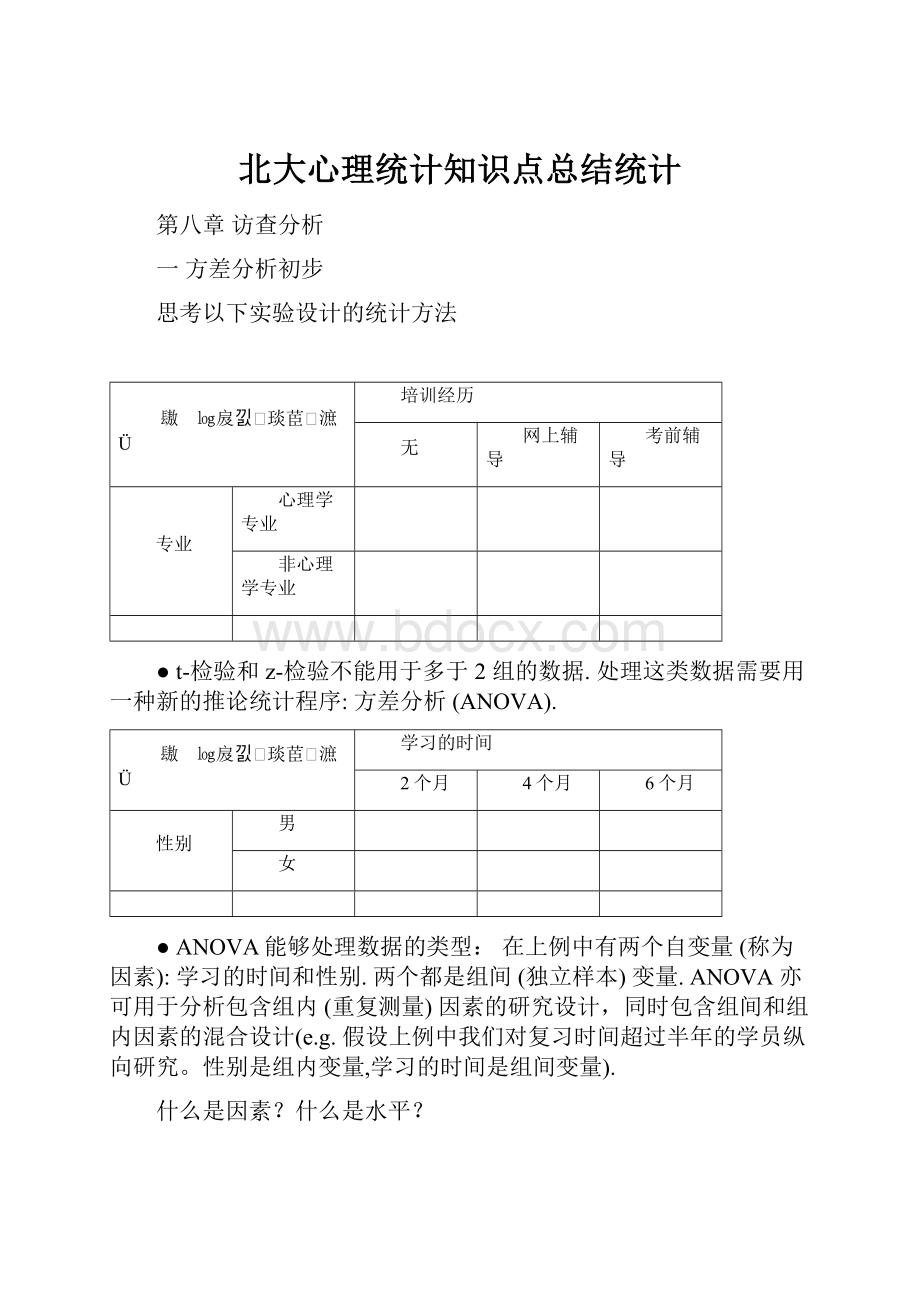
对于样本，计算F统计量

step6:

比较F统计量和临界F统计量

step7:

对于H0作出结论

单因素,独立测量研究设计的例子

●检验三个不同的学习方法的效应。

将学生随机分配到3个处理组

●方法A：

让学生只读课本,不去上课.

●方法B：

上课,记笔记，不读课本.

●方法C：

不读课本，不去上课,只看别人的笔记

●Step1:

陈述假设和设定标准（选择a）

H0:

μ1=μ2=μ3

H1:

其中一个组与另一个（或更多）的组均值不同。

备择假设可能的形式很多：

μ1不等于μ2=μ3

μ1=μ3不等于μ2

μ1=μ2不等于μ3

μ1不等于μ2不等于μ3

因此，只需给出虚无假设就够了

●step2:

ANOVA检验总是单尾.因为不存在负的方差.F分布表也只有单侧的Alpha.（F分布图）

●step3:

找出检验的df.注意要考虑几个df

●step4:

从表找出临界F统计量

与t分布表类似,F分布表也是描述一族F分布.

需要用到两个df,用一个找出正确的行另一个找出正确的列.上面一行对应于α=0.05,下面一行对应于α=0.01.

●step5:

计算样本的F统计量观测值

概念的水平的讨论：

ANOVA非常类似两个独立样本的t检验

tobs=得到的样本均值间差异

期望的机会差异

对于ANOVA检验统计量（称为F比率）类似

F=样本均值间方差（差异）

期望的机会（误差）方差（差异）

为什么用方差?

●

●因为有多于两个组.

●如何计算一个分数来描述差异间分布?

差异不能够分割,但是方差能够分割。

这就是ANOVA-方差分析名字的由来.

●首先考虑方差的来源.

●什么造成样本的不同（处理间变异）？

●处理/组效应-处理造成的差异

●个体差异效应-个体差异变异

●随机误差

●每一个样本内部的变异（处理内变异）

●个体差异效应

F比率可以表达为:

●F比率=样本均值间的方差（差异）

●期望的机会（误差）方差（差异）

●F比率=处理间方差

●处理内方差

●F比率=处理效应+个体差异+随机误差

●个体差异+随机误差

●注意:

有时分母叫做误差部分，其量度了由于机会造成的方差

如果H0为真,处理效应的值应该如何?

●H0:

μ1=μ2=μ3

●如果没有差异,效应方差=0

如果效应方差=0,F比率值?

●F比率=0+个体差异+随机误差=1.0个体差异+随机误差

●如果H0为假，F比率应该大于1.

●step6:

比较F统计量的观测值与临界F统计量

●如果F统计量的观测值（Fobs）在统计上显著地大于1.0则拒绝H0

ANOVA的专用符号

●K=处理条件（或组）的数目

●n=每一个组的数目（如果它们相等）

ni=第i组的数目（如果它们不等）

N=∑ni=总的样本容量

Ti=∑Xij

●G=∑Xij=总的和

G-bar=G/N=总的均值

●SSi=每一个组的和方=∑（Xij-Xi）2

●在上例中：

●∑X2=106

G=30=总的和

N=15=总的样本容量

G-bar=30/15=2=总的均值

K=3=处理条件（或组）的数目

ANOVA的过程和例题

●F比率=处理间方差

●处理内方差

●需要找出两个方差.

●最基本公式s2=SS/df.

●SS和=∑X2-（G2/N）

●SS和=106-（302/15）=106-60=46

●需要将其分解为组间变异和组内变异.

●SS和=SS组间+SS组内

●如何得到SS组内?

将每一个组SS相加

●SSwithin=∑SS每一个处理内部=∑SSi

●=6+6+4=16

如何得到SS组间?

●快捷的方法是:

●SS和-SS组内

●若数据足够，不推荐用这种方法,因为:

●无法检查计算错误

●未涉及SS组间是如何组成.

直接计算SS组间的两个公式:

定义公式和计算公式

●SS和=SS组间+SS组内=16+30=46

●s2=SS/df.

●已计算出SS,找出df:

●共有两个（或三个）自由度,一个组间方差df,一个组内方差df（以及一个总的df）.

●df和=N-1

●df组内==N-K

●df组间=K-1

●df和=df组内+df组间

●在例子中:

●df组内=15-3=12

●df组间=3-1=2

●df和=15-1=14,=12+2

●现在计算方差.这里称为均方.

●方差=均方=MS=SS/df

●MS组间=SS组间/df组内

●-->

上例中=30/2=15

有时MS组间称为误差的均方.

●MS组内=MS误差=误差的均方=SS组内/df组内

上例中=16/12=1.33

●F比率=处理间方差=MS组间

●处理内方差MSw组间

●上例中的F比率是:

15/1.33=11.28

方差分析表

查F表确定Fcrit

●查F表确定Fcrit对假设作出结论

●df组间=分子的df

df组内=分母的df（误差）

上例中:

●df组内=12;

df组间=2

●如果选择a=.05,Fcrit=3.88

如果选择a=.01,Fcrit=6.93

●F比率的观测值11.28大于Fcrit.,所以拒绝H0（m1=m2=m3）.

●报告结果

●F（df组间,df组内）=Fobs,p<

?

●"

单因素方差分析发现学习方法有显著的效应,F（2,12）=11.28,p<

0.01.

事后检验（Posthoctests）

●ANOVA的结果是检验H0:

μ1=μ2=μ3,这是一个两点（拒绝/不拒绝）决策.并未提供哪个备择假设得到支持.也就是说,只知道一些组与其它组不同,但并知道差别在哪些组之间.

●所以从ANOVA得到显著差异的结果（拒绝H0）后,一定要做作事后检验.事后检验使我们能够比较各组,发现差异产生在什么地方.

●事后检验就是比较每一个处理组与另一个处理组,一次比较两个.这称为成对比较.

在上例中,可以比较μ1与μ2,μ1与μ3,以及μ2与μ3.

●这样的做法有没有问题？

●每一个比较都是一个单独的假设检验,每一个都有犯I类错误的风险.所以,比较对数越多,作结论的风险越大。

即容易发现实际不存在的差异。

这称为实验导致的（experimentwise）alpha水平（或族系（familywise）误差）

αEW=1-（1-a）cc=比较对数

对于上述例子,如果选择a=0.05作3对比较

αEW=1-（1-a）c=1-（.95）3=1-.857=.143

●I类错误的机会增加到14.7%而不再是5%，多数事后检验设计中都控制了实验导致误差.

●这里介绍两个事后检验:

Tukey'

sHSD检验（honestly差异显著性）检验和Scheff检验.

Tukey'

sHSD检验

●可以计算出单一的值确定处理均值间的最小差异，考查此差异在统计上是否显著.

●此检验要求各组有相等的样本容量.

●HSD=q*sqrt（MS组内/n）

●q值可以从表中查出（附表6）.需要用到K和df组内,以及αEW

●在上例中（用αEW=.05）:

●HSD=q*sqrt（MS组内/n）=（3.77）sqrt（1.33/5）=（3.77）（.516）=1.94

●比较1:

μ1=μ2

●2-1=4.0-1.0=3.0

●HSD=1.94<

3.0，拒绝H0

●比较2:

μ1=μ3

●3-1=1.0-1.0=0.0

●HSD=1.94>

0.0，不能拒绝H0

●比较3:

μ2=μ3

●2-3=4.0-1.0=3.0

3.0，拒绝H0

●所以B与A和C不同，而A与C没有差异

Scheffe检验

●用F比率检验差异.这是最保守的检验（降低I类错误的风险,但增加II类错误的风险）.特别适用于n不等的情况

●重新计算MS组间,每次只检验一个比较.注意:

用整体的df组间和整体的MS组内

SS组间==52/5+202/5-252/10=22.5

MS组间==22.5/2=11.25

MS组内==16/12=1.33

F比率=MS间=11.25/1.33=8.46MS组内

查F表.a=.05,Fcrit（2,12）=3.88

8.46>

3.88,拒绝H0

μ1=μ3

SS组间==+-=0

MS组间==0/2=0

F比率=MS间=0/1.33=0MS组内

0<

3.88,不能拒绝H0

μ2=μ3

SS组间==52/5+202/5-252/10=22.5

F比率=MS间/MS组内=11.25/1.33=8.46

3.88,拒绝H0

方差分析与t-检验的关系

●差异间独立样本t-检验与两个水平的单因素组间ANOVA有和区别?

●没有.F比率=t2

●差异间t-检验和ANOVA,t-检验是考察两个均值间的差异ANOVA是考察方差.如果只有两个组,t统计量的平方就是F统计量.

方差分析的前提

●每个样本内的观察都是独立的

●样本所来自的总体为正态分布

●样本所来自的总体有相等的方差（方差一致性）

●一位研究者报告3*2的方差分析中，对其中一个因素主效应F检验的结果是F（2，24）=5.92。

根据此结果可知研究中有_____个被试。

二重复测量的方差分析

思考下面的实验设计

☐比较患有恐怖症的病人在治疗前、治疗后1周、治疗后1个月、治疗后1年的状况。

☐研究儿童1岁到3岁的记忆能力发展状况。

用方差分析解决多次重复测量的问题

●两次以上的重复测量若是用t检验则一类错误的风险累加

●方差分析对多次检验只用一个F比率,降低了一类风险。

重复测量与独立测量的区别

☐重复测量实验中始终用同一个样本，而独立测量是有几个处理用几个样本，肯定不等于一。

☐重复测量消除了处理间个体差异

☐重复测量的优点

⏹节省被试，降低研究成本

☐重复测量的缺点

⏹前一种处理会影响后一种处理

⏹疲劳

重复测量方差分析的主要任务

☐因为不存在了处理间的个体差异，那么应该在处理内也需要人为的去除个体间差异

重复测量方差分析之原理

☐因为最终是用F比率判断效果所以我们从F的分子与分母出发

☐分子：

处理间方差分为：

处理效果+随机误差—处理间方差可以由处理效果引起，随机误差引起。

但绝不肯能由个体间差异引起。

☐分母：

随机尺度内方差。

因为个体差异在分子中已经被自动消除，所以必须在分母中消除这个差异

重复测量的公式推导与符号

处理间方差的推导与独立测量分子完全相同。

☐分母:

处理内方差减去个体间方差叫做剩余方差（residualvariance\errorvariance）

•与独立测量方差分析的符号基本相同，只有一个新符号P

•P:

每个个体的处理间分数和

•T纵向的，P是横向的。

重复测量方差分析假设检验的步骤

☐STEP1确定假设，确定α值

⏹虚无假设H0：

μ1=μ2=μ3

⏹备择假设H1：

至少有一个处理的均值不同于其它

☐STEP2计算自由度，确定临界值

⏹dfbetweentreatment=k-1

⏹Dferror=（N-k）-（n-1）

☐STEP3计算各个统计量为F比率的计算做准备：

最好列张表

例题

☐

☐∑X2=140

G=36

☐K=3，n=4，N=12

☐第1阶段：

SS和=SS组间+SS组内

⏹SS和=∑X2-（G2/N）

⏹SS和=140-（362/12）=140-108=32

⏹需要将其分解为组间变异和组内变异.

⏹SS组间=S（T2/ni）-G2/N

⏹=82/4+202/4+182/4–108=14

⏹SS组内=∑SS每一个处理内部=∑SSi=2+5+11=18

☐第2阶段：

⏹SS组内=SS被试间+SS误差

⏹SS被试间=S（P2/k）-G2/N

⏹=122/3+62/3+62/3+122/3–108=12

⏹SS误差=SS组内-SS被试间=18-12=6

计算均方和F值

☐均方和F值的计算.

☐MS=SS/df

☐MS组间=SS组间/df组间

☐-->

上例中=14/2=7

☐MS误差=SS误差/df误差

上例中=6/6=1

☐F比率=处理间方差

误差方差

做结论

☐查F表确定Fcrit对假设作出结论

⏹df组间=分子的df

⏹-->

⏹df误差=6;

df组间=3

⏹假设中选择a=.05,Fcrit=4.76

（如果选择a=.01,Fcrit=9.78）

⏹F比率的观测值6大于F.05.,所以拒绝H0

☐报告结果

⏹F（df组间,df误差）=Fobs,p<

⏹各练习次数的均值和标准差列在表1中。

重复测量的方差分析发现练习次数有显著的效应,F（2,6）=6,p<

0.05.

重复测量的事后检验

☐Tukey’HSD和Scheffe检验都还和以往独立测量的相同，只是这里把公式中的MSwithin换成MSerror,查表时也是把dfwithin换成dfrror。

练习题

总结

☐重复测量方差分析可以被看成两个分两个步骤的分析。

第一个步骤和独立的方差分析相同，将总体的方差分为两部分：

处理间的和处理内的。

由于在各个处理条件下用的是同一组被试，所以处理间的成分不包含被试的差异。

然而处理内的成分包含个体差异，为了得到实验误差，在第二个步骤中必需将个体差异去掉。

☐F=处理间方差（不包含个体差异）

实验误差（排除了个体差异）

☐和方的计算

☐SS误差和df误差的计算

☐自由度的计算

☐事后检验

☐重复测量的方差分析和独立测量的方差分析的比较

三二因素方差分析

previw

☐一个社会心理学的实验设计

☐自变量1：

信息发布者的吸引力

☐自变量2：

沟通的呈现方式

☐因变量：

态度改变的大小

overview

☐方差分析

⏹单因素研究设计

⏹因素设计

☐本章所涉及的因素设计

⏹二因素

⏹独立测量

⏹每组被试数相同

例子：

研究工人的工作效率

因素B:

温度

70度

80度

90度

因素A:

湿度

30%的湿度

15个被试的分数

70%的湿度

☐二因素方差分析的目的

⏹湿度的两个水平上的平均数差异

⏹温度的三个水平上的平均数差异

⏹特定的温度和特定的湿度的组合造成的平均数的差异

☐原理

⏹在一次分析中包含三个不同的假设检验

⏹这三个假设检验有不同的F比率

⏹F=variance（differences）betweensamplemeans

variance（differences）expectedbychance

主效应

☐前面的例子：

2X3的因素设计

☐主效应：

⏹因素a:

湿度．两个水平之间的平均数差异

⏹因素b：

温度．三个水平的平均数之间的差异

交互作用的定义　

☐在每个某个因素的某个水平下平均数的差异不能被该因素总体的平均数差异所预测．

☐当一个因素的效应的大小依赖于另一个因素的不同水平，那么就存在交互作用．

交互作用的图解

因素a与因素b不存在交互作用（１）

因素a与因素b不存在交互作用（２）

因素a与因素b存在交互作用

实际研究的例子

☐紧张状况对完成任务效果的影响

☐紧张状况：

弱　中等　强

☐任务类型：

简单　复杂

作图在二因素方差分析中的作用　　

☐如何做图

⏹一个因素用横坐标表示

⏹另一个直接在线上进行标定

☐可以大致判断一下是否存在交互作用

⏹两条线是否平行？

☐每个因素的是否存在主效应

⏹横作标上的因素：

线是否水平

⏹标的因素：

两条线的重合度

虚无假设

☐因素A的主效应

μA1=μA2

☐因素B的主效应

μB1=μB2=μB3

☐交互作用

因素A和因素B之间没有交互作用。

所有处理条件之间的差异能用两个因素的主效应解释。

和方的第二阶段分解

☐和方的第一阶段分解:

☐总和方=处理间和方+处理内和方

☐和方的第二阶段分解：

☐处理间和方

☐=A的主效应+B的主效应+AXB交互作用

☐三个F比率可以表达为:

☐误差方差

☐FAXB=AXB交互作用

如何作假设检验

☐先考察交互作用

☐如果交互作用显著,主效应就难于解释

☐然后考察主效应

☐一定要作图以直观表示结果

因素设计ANOVA的符号

☐a：

A因素的水平数

☐b：

B因素的水平数

☐A1B2：

在单位格A1B2中分数的和

☐A1：

在所有A1处理中分数的和

☐例：

根据心理学原理，测验条件与学习条件一致时，学习效果最好。

以下数据是否显示了教室与考场大小对测验成绩有无显著差异

虚无假设

☐教室大小对成绩没有显著影响

☐Ho：

μa1=μa2；

H1：

μa1≠μa2

☐考场大小对成绩没有显著影响

μb1=μb2；

μb1≠μb2

☐考场大小对成绩的影响不因教室大小而不同

☐三者均以=.05为标准

自由度

☐dfa=a-1=2-1=1

☐dfb=b-1=2-1=1

☐dfaxb=（a-1）（b-1）=（2-1）（2-1）=1

☐Df处理内=N-ab=20-2*2=16

☐FcritA=FcritB=FcritAXB=4.49

☐方差分析准备

☐计算各组的统计量，G和ΣX2

☐和方分解第一阶段

☐SS总和=

☐SS处理间=ΣAB2/n–G2/N

☐SS处理内=

☐和方分解第二阶段

☐SSA=ΣA2/bn–G2/N

☐SSB=ΣB2/an–G2/N

☐SSAxB=SS处理间–SSA–SSB

方差分析表

结论

☐A因