八年级数学上全等三角形 轴对称期末复习提优题及答案解析文档格式.docx

八年级数学上全等三角形 轴对称期末复习提优题及答案解析文档格式.docx

《八年级数学上全等三角形 轴对称期末复习提优题及答案解析文档格式.docx》由会员分享，可在线阅读，更多相关《八年级数学上全等三角形 轴对称期末复习提优题及答案解析文档格式.docx（37页珍藏版）》请在冰豆网上搜索。

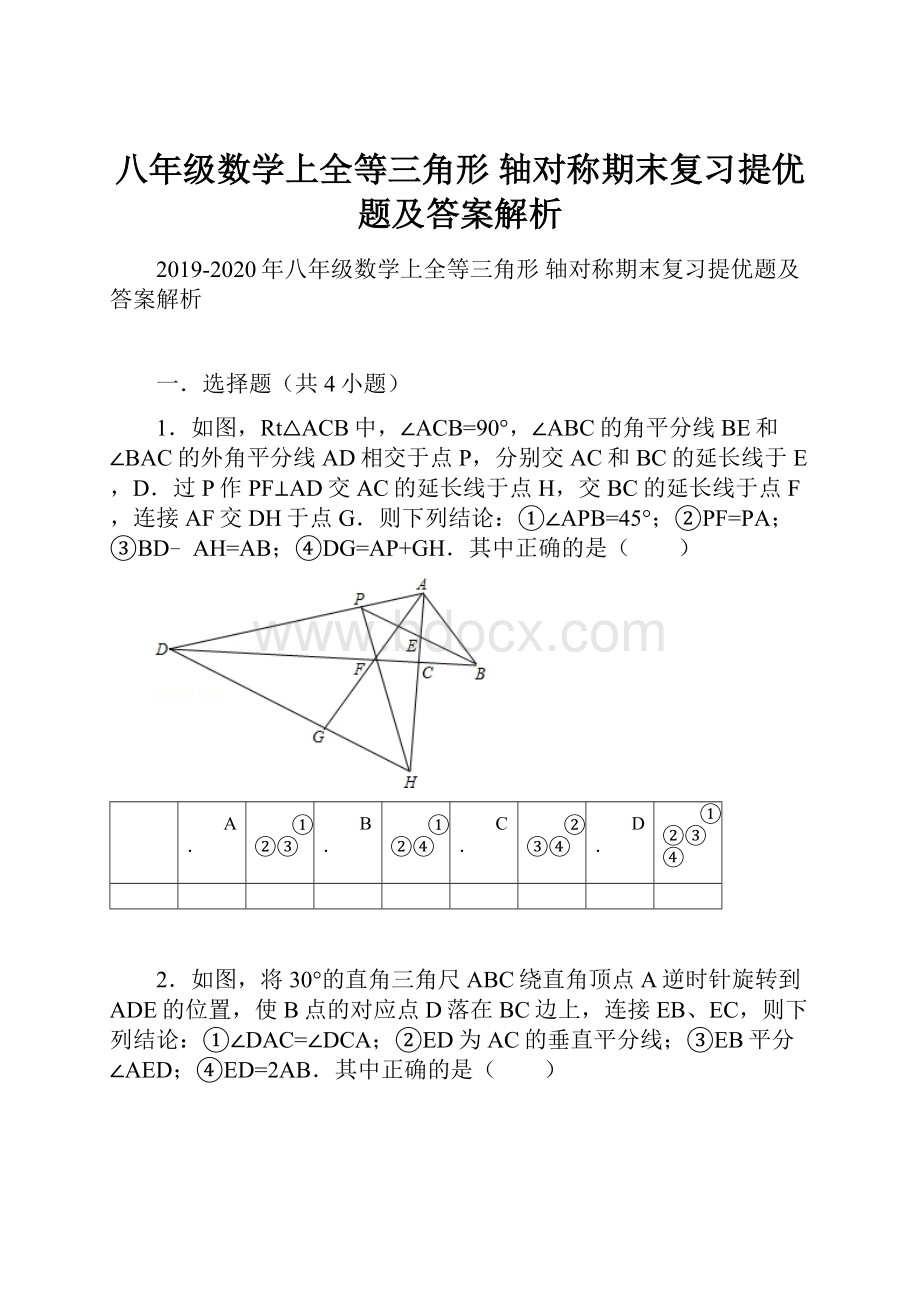
其中正确的有（　　）

2个

3个

4个

5个

二．解答题（共8小题）

5．如图1，在Rt△ACB中，∠ACB=90°

，∠ABC=30°

AC=1点D为AC上一动点，连接BD，以BD为边作等边△BDE，EA的延长线交BC的延长线于F，设CD=n，

（1）当n=1时，则AF=　_________　；

（2）当0＜n＜1时，如图2，在BA上截取BH=AD，连接EH，求证：

△AEH为等边三角形．

6．两个等腰直角△ABC和等腰直角△DCE如图1摆放，其中D点在AB上，连接BE．

（1）则

=　_________　，∠CBE=　_________　度；

（2）当把△DEF绕点C旋转到如图2所示的位置时（D点在BC上），连接AD并延长交BE于点F，连接FC，则

=　_________　，∠CFE=　_________　度；

（3）把△DEC绕点C旋转到如图3所示的位置时，请求出∠CFE的度数　_________　．

7．已知△ABC为边长为10的等边三角形，D是BC边上一动点：

①如图1，点E在AC上，且BD=CE，BE交AD于F，当D点滑动时，∠AFE的大小是否变化？

若不变，请求出其度数．

②如图2，过点D作∠ADG=60°

与∠ACB的外角平分线交于G，当点D在BC上滑动时，有下列两个结论：

①DC+CG的值为定值；

②DG﹣CD的值为定值．其中有且只有一个是正确的，请你选择正确的结论加以证明并求出其值．

8．如图，点A、C分别在一个含45°

的直角三角板HBE的两条直角边BH和BE上，且BA=BC，过点C作BE的垂线CD，过E点作EF上AE交∠DCE的角平分线于F点，交HE于P．

（1）试判断△PCE的形状，并请说明理由；

（2）若∠HAE=120°

，AB=3，求EF的长．

9．如图，AD是△ABC的角平分线，H，G分别在AC，AB上，且HD=BD．

（1）求证：

∠B与∠AHD互补；

（2）若∠B+2∠DGA=180°

，请探究线段AG与线段AH、HD之间满足的等量关系，并加以证明．

10．如图，在等腰Rt△ABC与等腰Rt△DBE中，∠BDE=∠ACB=90°

，且BE在AB边上，取AE的中点F，CD的中点G，连接GF．

（1）FG与DC的位置关系是　_________　，FG与DC的数量关系是　_________　；

（2）若将△BDE绕B点逆时针旋转180°

，其它条件不变，请完成下图，并判断

（1）中的结论是否仍然成立？

请证明你的结论．

11．如图1，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．

（1）试探究EP与FQ之间的数量关系，并证明你的结论．

（2）若连接EF交GA的延长线于H，由

（1）中的结论你能判断并证明EH与FH的大小关系吗？

（3）图2中的△ABC与△AEF的面积相等吗？

（不用证明）

12．已知如图1：

△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．

①图中有几个等腰三角形？

请说明EF与BE、CF间有怎样的关系．

②若AB≠AC，其他条件不变，如图2，图中还有等腰三角形吗？

如果有，请分别指出它们．另第①问中EF与BE、CF间的关系还存在吗？

③若△ABC中，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．如图3，这时图中还有哪几个等腰三角形？

EF与BE、CF间的关系如何？

为什么？

八年级[丄]数学期末《全等三角形》《轴对称》复习提优题【大海之音组卷】

参考答案与试题解析

考点：

直角三角形的性质；

角平分线的定义；

垂线；

全等三角形的判定与性质．

专题：

推理填空题．

分析：

①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP，再根据角平分线的定义∠ABP=

∠ABC，然后利用三角形的内角和定理整理即可得解；

②③先根据直角的关系求出∠AHP=∠FDP，然后利用角角边证明△AHP与△FDP全等，根据全等三角形对应边相等可得DF=AH，对应角相等可得∠PFD=∠HAP，然后利用平角的关系求出∠BAP=∠BFP，再利用角角边证明△ABP与△FBP全等，然后根据全等三角形对应边相等得到AB=BF，从而得解；

④根据PF⊥AD，∠ACB=90°

，可得AG⊥DH，然后求出∠ADG=∠DAG=45°

，再根据等角对等边可得DG=AG，再根据等腰直角三角形两腰相等可得GH=GF，然后求出DG=GH+AF，有直角三角形斜边大于直角边，AF＞AP，从而得出本小题错误．

解答：

解：

①∵∠ABC的角平分线BE和∠BAC的外角平分线，

∴∠ABP=

∠ABC，

∠CAP=

（90°

+∠ABC）=45°

+

在△ABP中，∠APB=180°

﹣∠BAP﹣∠ABP，

=180°

﹣（45°

∠ABC+90°

﹣∠ABC）﹣

﹣45°

﹣

∠ABC﹣90°

+∠ABC﹣

=45°

，故本小题正确；

②③∵∠ACB=90°

，PF⊥AD，

∴∠FDP+∠HAP=90°

，∠AHP+∠HAP=90°

，

∴∠AHP=∠FDP，

∵PF⊥AD，

∴∠APH=∠FPD=90°

在△AHP与△FDP中，

∴△AHP≌△FDP（AAS），

∴DF=AH，

∵AD为∠BAC的外角平分线，∠PFD=∠HAP，

∴∠PAE+∠BAP=180°

又∵∠PFD+∠BFP=180°

∴∠PAE=∠PFD，

∵∠ABC的角平分线，

∴∠ABP=∠FBP，

在△ABP与△FBP中，

∴△ABP≌△FBP（AAS），

∴AB=BF，AP=PF故②小题正确；

∵BD=DF+BF，

∴BD=AH+AB，

∴BD﹣AH=AB，故③小题正确；

④∵PF⊥AD，∠ACB=90°

∴AG⊥DH，

∵AP=PF，PF⊥AD，

∴∠PAF=45°

∴∠ADG=∠DAG=45°

∴DG=AG，

∵∠PAF=45°

，AG⊥DH，

∴△ADG与△FGH都是等腰直角三角形，

∴DG=AG，GH=GF，

∴DG=GH+AF，

∵AF＞AP，

∴DG=AP+GH不成立，故本小题错误，

综上所述①②③正确．

故选A．

点评：

本题考查了直角三角形的性质，全等三角形的判定，以及等腰直角三角形的判定与性质，等角对等边，等边对等角的性质，综合性较强，难度较大，做题时要分清角的关系与边的关系．

旋转的性质；

含30度角的直角三角形．

根据直角三角形中30°

的角所对的直角边等于斜边的一半，以及旋转的性质即可判断．

①根据旋转的性质可以得到：

AB=AD，而∠ABD=60°

，则△ABD是等边三角形，可得到∠DAC=30°

，∴∠DAC=∠DCA，故正确；

②根据①可得AD=CD，并且根据旋转的性质可得：

AC=AE，∠EAC=60°

，则△ACE是等边三角形，则EA=EC，即D、E都到AC两端的距离相等，则DE在AC的垂直平分线上，故正确；

③根据条件AB∥DE，而AB≠AE，即可证得EB平分∠AED不正确，故错误；

④根据旋转的性质，DE=BC，而BC=2AB，即可证得ED=2AB，故正确；

故正确的是：

①②④．故选B．

正确理解旋转的性质，图形旋转前后两个图形全等是解决本题的关键．

全等三角形的判定与性质；

等腰三角形的性质．

根据三角形全等的判定和性质以及三角形内角和定理逐条分析判断．

在△ABC中，AD、BE分别平分∠BAC、∠ABC，

∵∠ACB=90°

∴∠A+∠B=90°

又∵AD、BE分别平分∠BAC、∠ABC，

∴∠BAD+∠ABE=

（∠A+∠B）=45°

∴∠APB=135°

，故①正确．

∴∠BPD=45°

又∵PF⊥AD，

∴∠FPB=90°

+45°

=135°

∴∠APB=∠FPB，

又∵∠ABP=∠FBP，

BP=BP，

∴△ABP≌△FBP，

∴∠BAP=∠BFP，AB=FB，PA=PF，故②正确．

在△APH和△FPD中，

∵∠APH=∠FPD=90°

∠PAH=∠BAP=∠BFP，

PA=PF，

∴△APH≌△FPD，

∴AH=FD，

又∵AB=FB，

∴AB=FD+BD=AH+BD．故③正确．

∵△ABP≌△FBP，△APH≌△FPD，

∴S四边形ABDE=S△ABP+S△BDP+S△APH﹣S△EOH+S△DOP=S△ABP+S△ABP﹣S△EOH+S△DOP=2S△ABP﹣S△EOH+S△DOP

．

故选C．

本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：

SSS、SAS、ASA、AAS、HL．

注意：

AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

角平分线的性质．

过M作ME⊥AD于E，得出∠MDE=

∠CDA，∠MAD=

∠BAD，求出∠MDA+∠MAD=

（∠CDA+∠BAD）=90°

，根据三角形内角和定理求出∠AMD，即可判断①；

根据角平分线性质求出MC=ME，ME=MB，即可判断②和⑤；

由勾股定理求出DC=DE，AB=AE，即可判断③；

根据SSS证△DEM≌△DCM，推出S三角形DEM=S三角形DCM，同理得出S三角形AEM=S三角形ABM，即可判断④．

过M作ME⊥AD于E，

∵∠DAB与∠ADC的平分线相交于BC边上的M点，

∴∠MDE=

∠BAD，

∵DC∥AB，

∴∠CDA+∠BAD=180°

∴∠MDA+∠MAD=

（∠CDA+∠BAD）=

×

180°

=90°

∴∠AMD=180°

﹣90°

，∴①正确；

∵DM平分∠CDE，∠C=90°

（MC⊥DC），ME⊥DA，

∴MC=ME，

同理ME=MB，

∴MC=MB=ME=

BC，∴②正确；

∴M到AD的距离等于BC的一半，∴⑤正确；

∵由勾股定理得：

DC2=MD2﹣MC2，DE2=MD2﹣ME2，

又∵ME=MC，MD=MD，

∴DC=DE，

同理AB=AE，

∴AD=AE+DE=AB+DC，∴③正确；

∵在△DEM和△DCM中

∴△DEM≌△DCM（SSS），

∴S三角形DEM=S三角形DCM

同理S三角形AEM=S三角形ABM，

∴S三角形AMD=

S梯形ABCD，∴④正确；

故选D．

本题考查了角平分线性质，垂直定义，直角梯形，勾股定理，全等三角形的性质和判定等知识点的应用，主要考查学生运用定理进行推理的能力．

（1）当n=1时，则AF=　2　；

含30度角的直角三角形；

等边三角形的性质．

动点型．

（1）根据三角形内角和定理求出∠BAC=60°

，再根据平角等于180°

求出∠FAC=60°

，然后求出∠F=30°

，根据30°

角所对的直角边等于斜边的一半求解即可；

（2）根据三角形的任意一个外角等于与它不相邻的两个内角的和利用∠CBD表示出∠ADE=30°

+∠CBD，又∠HBE=30°

+∠CBD，从而得到∠ADE=∠HBE，然后根据边角边证明△ADE与△HBE全等，根据全等三角形对应边相等可得AE=HE，对应角相等可得∠AED=∠HEB，然后推出∠AEH=∠BED=60°

，再根据等边三角形的判定即可证明．

（1）解：

∵△BDE是等边三角形，

∴∠EDB=60°

∴∠BAC=180°

﹣30°

=60°

∴FAC=180°

﹣60°

∴∠F=180°

=30°

∴∠ACF=180°

∴AF=2AC=2×

1=2；

（2）证明：

∴BE=BD，∠EDB=∠EBD=60°

在△BCD中，∠ADE+∠EDB=∠CBD+∠C，

即∠ADE+60°

=∠CBD+90°

∴∠ADE=30°

+∠CBD，

∵∠HBE+∠ABD=60°

，∠CBD+∠ABD=30°

∴∠HBE=30°

∴∠ADE=∠HBE，

在△ADE与△HBE中，

∴△ADE≌△HBE（SAS），

∴AE=HE，∠AED=∠HEB，

∴∠AED+∠DEH=∠DEH+∠HEB，

即∠AEH=∠BED=60°

∴△AEH为等边三角形．

本题考查了30°

角所对的直角边等于斜边的一半的性质，全等三角形的判定与性质，等边三角形的性质与判定，以及三角形的一个外角等于与它不相邻的两个内角的和的性质，

（2）中求出

∠ADE=∠HBE是解题的关键．

=　1　，∠CBE=　45　度；

=　1　，∠CFE=　45　度；

（3）把△DEC绕点C旋转到如图3所示的位置时，请求出∠CFE的度数　135°

　．

圆周角定理；

等腰直角三角形；

确定圆的条件．

（1）先证明∠ACD=∠BCE，再根据边角边定理证明△ACD≌△BCE，然后根据全等三角形对应边相等和对应角相等解答；

（2）根据

（1）的思路证明△ACD和△BCE全等，再根据全等三角形对应边相等得BE=AD，对应角相等得∠DAC=∠DBF，又AC⊥CD，所以AF⊥BF，从而可以得到C、E、F、D四点共圆，根据同弧所对的圆周角相等即可求出∠CFE=∠CDE=45°

（3）同

（2）的思路，证明C、F、D、E四点共圆，得出∠CFD=∠CED=45°

，而∠DEF=90°

，所以∠CFE的度数即可求出．

（1）∵△ABC和△DCE是等腰三角形，

∴AC=BC，CD=CE，

∵∠ACB=∠DCE=90°

∴∠ACB﹣∠BCD=∠DCE﹣∠BCD，

即∠ACD=∠BCE，

在△ACD和△BCE中，

∴△ACD≌△BCE（SAS），

∴BE=AD，∠CBE=∠CAD=45°

因此

=1，∠CBE=45°

wWw.

（2）同

（1）可得BE=AD，

∴

=1，

∠CBE=∠CAD；

又∵∠ACD=90°

，∠ADC=∠BDF，

∴∠BFD=∠ACD=90°

又∵∠DCE=90°

∴C、E、F、D四点共圆，

∴∠CFE=∠CDE=45°

（3）同

（2）可得∠BFA=90°

∴∠DFE=90°

∴C、F、D、E四点共圆，

∴∠CFD=∠CED=45°

∴∠CFE=∠CFD+∠DFE

+90°

本题综合考查了等边对等角的性质，三角形全等的判定和全等三角形的性质，四点共圆以及同弧所对的圆周角相等的性质，需要熟练掌握并灵活运用．

等边三角形的性质；

探究型．

①∠AFE的大小不变，其度数为60°

，理由如下：

由三角形ABC为等边三角形，得到三条边相等，三个内角相等，都为60°

，可得出AB=BC，∠ABD=∠C，再由BD=CE，利用SAS可得出三角形ABD与三角形BCE全等，根据全等三角形的对应角相等可得出∠BAD=∠CBE，在三角形ABD中，由∠ABD为60°

，得到∠BAD+∠ADB的度数，等量代换可得出∠CBE+∠ADB的度数，利用三角形的内角和定理求出∠BFD的度数，根据对应角相等可得出∠AFE=∠BFD，可得出∠AFE的度数不变；

②连接AG，如图所示，由三角形ABC为等边三角形，得出三条边相等，三个内角都相等，都为60°

，再由CG为外角平分线，得出∠ACG也为60°

，由∠ADG为60°

，可得出A，D，C，G四点共圆，根据圆内接四边形的对角互补可得出∠DAG与∠DCG互补，而∠DCG为120°

，可得出∠DAG为60°

，根据∠BAD+∠DAC=∠DAC+∠CAG=60°

，利用等式的性质得到∠BAD=∠CAG，利用ASA可证明三角形ABD与三角形ACG全等，利用全等三角形的对应边相等可得出BD=CG，由BC=BD+DC，等量代换可得出CG+CD=BC，而BC=10，即可得到DC+CG为定值10，得证．

，理由为：

∵△ABC为等边三角形，

∴AB=BC，∠ABD=∠C=60°

在△ABD和△BCE中，

∴△ABD≌△BCE（SAS），

∴∠BAD=∠CBE，

又∠BAD+∠ADB=120°

∴∠CBE+∠ADB=120°

∴∠BFD=60°

则∠AFE=∠BFD=60°

②正确的结论为：

DC+CG的值为定值，理由如下：

连接AG，如图2所示：

∴AB=BC=AC，∠ABD=∠ACB=∠BAC=60°

又CG为∠ACB的外角平分线，

∴∠ACG=60°

又∵∠ADG=60°

∴∠ADG=∠ACG，即A，D，C，G四点共圆，

∴∠DAG+∠DCG=180°

，又∠DCG=120°

∴∠DAG=60°

，即∠DAC+∠CAG=60°

又∵∠BAD+∠DAC=60°

∴∠BAD=∠GAC，

在△ABD和△ACG中，

∵

∴△ABD≌△ACG（ASA），

∴DB=GC，又BC=10，

则BC=BD+DC=DC+CG=10，即DC+CG的值为定值．

此题考查了等边三角形的判定与性质，全等三角形的判定与性质，四点共圆的条件，以及圆内接四边形的性质，利用了等量代换及转化的思想，熟练掌握等边三角形的判定与性质是解本题的关键．

等腰直角三角形．

计算题；

证明题．

（1）根据∠PCE=

∠DCE=

90°

，求证∠CPE=90°

，然后即可判断三角形的形状．

（2）根据∠HEB=∠H=45°

得HB=BE，再根据BA=BC和∠HAE=120