人教版七年级数学下册第十章数据的收集整理与描述第三节从数据谈节水单元复习与测试题含答案 16文档格式.docx
《人教版七年级数学下册第十章数据的收集整理与描述第三节从数据谈节水单元复习与测试题含答案 16文档格式.docx》由会员分享,可在线阅读,更多相关《人教版七年级数学下册第十章数据的收集整理与描述第三节从数据谈节水单元复习与测试题含答案 16文档格式.docx(17页珍藏版)》请在冰豆网上搜索。
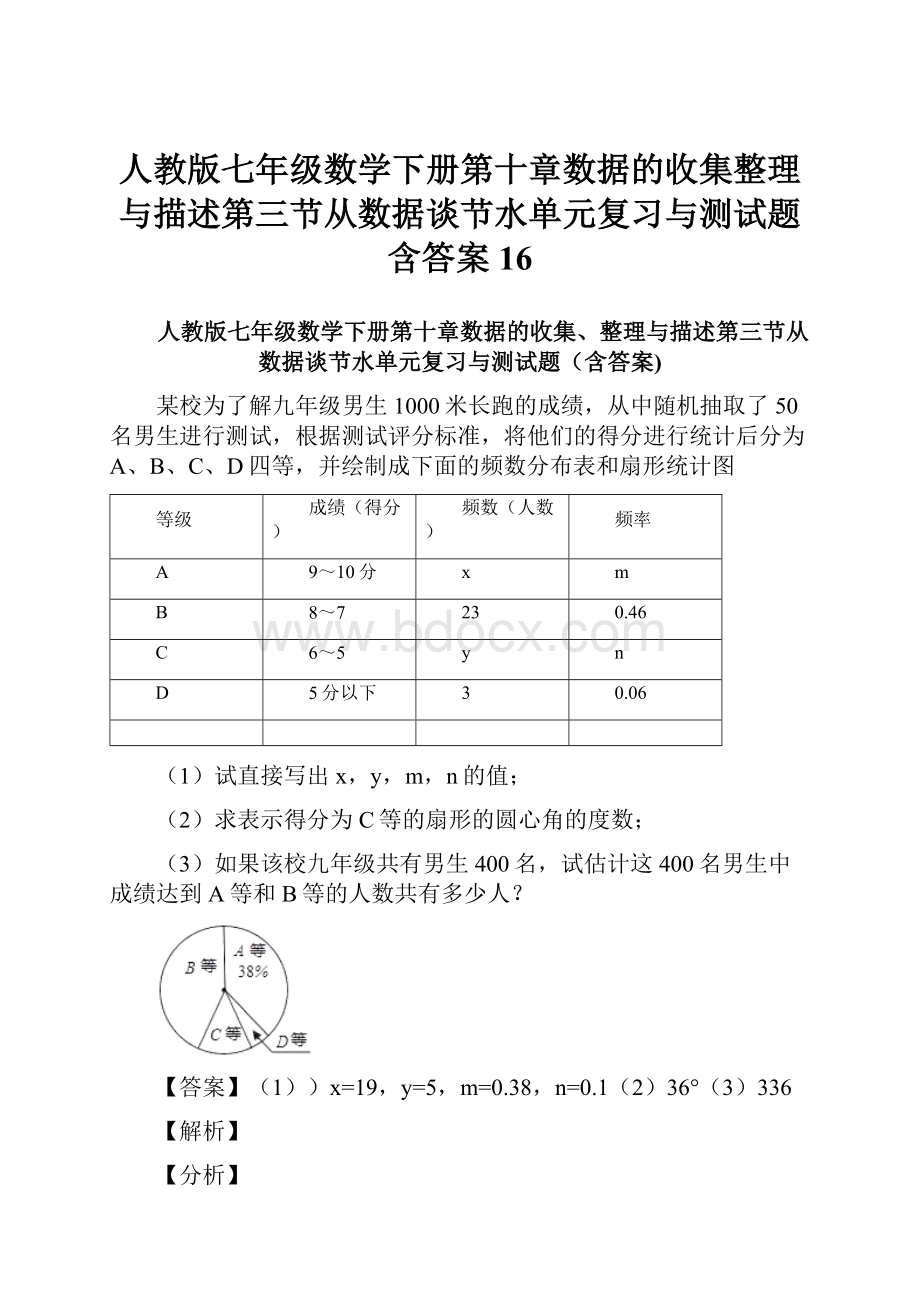
(3)用总人数乘以A、B的频率和即可得.
【详解】
解:
(1)∵样本容量为23÷
0.46=50,m=38%=0.38,
∴x=50×
0.38=19,y=50﹣19﹣23﹣3=5,
则n=5÷
50=0.1;
(2)表示得分为C等的扇形的圆心角的度数为360°
×
0.1=36°
;
(3)估计这400名男生中成绩达到A等和B等的人数共有400×
(0.38+0.46)=336(人).
【点睛】
此题考查了频数(率)分布表,用样本估计总体,以及扇形统计图,弄清题中的数据是解本题的关键.
52.盐城市明达中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现抽查了九年级
(1)班全班同学捐款情况,并绘制出如下的统计表和统计图:
捐款(元)
20
50
100
150
200
人数(人)
4
12
9
2
求:
(1)m= ,n= ;
(2)求学生捐款数目的众数、中位数和平均数;
(3)若该校有学生3500人,估计该校学生共捐款多少元?
(1)40,30;
(2)众数是50元,中位数为50元,平均数81元;
(3)估计该校学生共捐款283500元
(1)把表格中的数据相加得出本次接受随机抽样调查的学生人数;
利用50元,100元的捐款人数求得占总数的百分比得出m、n的数值即可;
(2)利用众数、中位数和平均数的意义和求法分别得出答案即可;
(3)利用求得的平均数乘总人数得出答案即可.
(1)本次接受随机抽样调查的学生人数为4+12+9+3+2=30人.
12÷
30=40%,9÷
30=30%,
所以扇形统计图中的m=40,n=30;
故答案为40,30;
(2)∵在这组数据中,50出现了12次,出现的次数最多,
∴学生捐款数目的众数是50元;
∵按照从小到大排列,处于中间位置的两个数据都是50,
∴中位数为50元;
这组数据的平均数=(20×
4+50×
12+100×
9+150×
3+200×
2)÷
30=2430÷
30=81(元).
(3)根据题意得:
3500×
81=283500元
答:
估计该校学生共捐款283500元.
考查扇形统计图,用样本估计总体,众数、中位数、平均数的意义与求法,理解题意,从图表中得出数据以及利用数据运算的方法是解决问题的关键.
53.某校为了解九年级学生的
身体素质情况,体育老师对九
(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第
A
10分
7
0.14
9分
x
m
B
8分
15
0.30
7分
8
0.16
C
6分
4
0.08
5分
y
n
3
0.06
合计
50
1
(1)直接写出:
m,x,y;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
(1)x=11,y=2,m=0.22;
(2)C等扇形的圆心角的度数为43.2度;
(3)这700名学生中成绩达到A等和B等的人数共有574人.
(1)根据扇形统计图求出A等的人数,再减去得10分的人数即可求出x值与频率m值,再用总人数减去各分值人数求出y值;
(2)先求出n的值,再求出C组的占比,即可求出其圆心角度数;
(3)根据A组,B组的频率即可估计这700名学生中成绩达到A等和B等的人数.
(1)x=50×
36%﹣7=11,
y=50-(7+11+15+8+4+3)=2,
m=11÷
50=0.22;
(2)∵n=2÷
50=0.04,
∴C等扇形的圆心角的度数为:
(0.08+0.04)×
360°
=43.2度;
(3)达到A等和B等的人数为:
(0.14+0.22+0.3+0.16)×
700=574人.
这700名学生中成绩达到A等和B等的人数共有574人.
此题主要考查扇形统计图与表格的应用,解题的关键是先根据各占比求出其人数.
54.我市某化工厂从2015年开始节能减排,控制二氧化硫的排放.如图分别是该厂2015~2018年二氧化硫排放量(单位:
吨)的两幅不完整的统计图,根据图中信息回答下列问题.
(1)求该厂2015~2018年二氧化硫排放总量;
(2)把图中折线统计图补充完整.
(1)100(吨);
(2)见解析
(1)根据扇形统计图折线统计图可求出该厂2015-2018年二氧化硫的排放总量,然后分别求出这四年的排放量即可得出这四年平均每年二氧化硫排放量;
(2)根据求出的四年的排放量可补全折线图.
(1)解:
(1)∵该厂2016年二氧化硫的排放量20吨,占2015-2018年二氧化硫的排放总量的20%.
∴该厂2015-2018年二氧化硫的排放总量是20÷
20%=100(吨).
(2)
本题考查了扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°
的比.
55.武汉市某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷词查的结果分为“非常了解“、“比较了解”、“只听说过”,“不了解”四个等级,划分等级后的数据整理如下表:
非常了解
比较了解
只听说过
不了解
频数
40
120
36
4
0.2
0.18
0.02
(1)本次问卷调查取样的样本容量为,表中的m值为;
(2)在扇形图中完善数据,写出等级及其百分比;
根据表中的数据计算等级为“非常了解”的频数在扇形统计图所对应的扇形的圆心角的度数;
(3)若该校有学生1500人,请根据调查结果估计这些学生中“比较了解”垃圾分类知识的人数约为多少?
(1)200;
0.6
(2)非常了解20%,比较了解60%;
72°
(3)900人
(1)根据非常了解的频数与频率即可求出本次问卷调查取样的样本容量,用1减去各等级的频率即可得到m值;
(2)根据非常了解的频率、比较了解的频率即可求出其百分比,与非常了解的圆心角度数;
(3)用全校人数乘以非常了解的频率即可.
(1)本次问卷调查取样的样本容量为40÷
0.2=200;
m=1-0.2-0.18-0.02=0.6
(2)非常了解20%,比较了解60%;
非常了解的圆心角度数:
20%=72°
(3)1500×
60%=900(人)
“比较了解”垃圾分类知识的人数约为900人.
此题主要考查扇形统计图的应用,解题的关键是根据频数与频率求出调查样本的容量.
56.今年,市政府的一项实事工程就是由政府投人1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_______户;
(2)改造后,一只水龙头一年大约可节省5t水,一只马桶一年大约可节省15t水,试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
【答案】
(1)1000;
(2)20850吨;
(3)既要改造水龙头又要改造马桶的家庭共有63户.
(1)根据随机抽样的120户中有20户不需要改造可以得到答案
(2)先根据抽样的120户家庭算出节水量,再计算该社区总量(3)设既要改造水龙头又要改造马桶的家庭为x,根据题意列一元一次方程解答即可.
(1)随机抽样的120户中有20户不需要改造,所以估计该社区需要对水龙头、马桶进行改造的家庭共有1000户,故答案为1000
(2)抽样的120户家庭一年共可节约用水:
(t).
∴该社区一年共可节约用水的吨数为:
2085×
=20850(t).
(3)设既要改造水龙头又要改造马桶的家庭共有x户,则只改造水龙头不改造马桶的家庭共有(92-x)户,只改造马桶不改造水龙头的家庭共有(71-x)户,根据题意列方程,得x+(92-x)+(71-x)=100,
解得x=63.
既要改造水龙头又要改造马桶的家庭共有63户.
也可以从另一角度考虑,从表中数据可以看出,在这120户中,改造水龙头和改造马桶的户数之和为31+28+21+12+69+2=163(户),
由于只有100户需要对水龙头、马桶进行改造,所以多出的就是既要改造水龙头又要改造马桶的家庭,因此,此类家庭的户数为163-100=63(户).
此题重点考察学生对统计表的综合应用能力,把握抽样调查的方式,会列方程是解题的关键.
57.某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分:
类别
E
节目类型
新闻
体育
动画
娱乐
戏曲
人数
12
30
54
9
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有多少人,这些学生数占被调查总人数的百分比为多少;
(2)被调查学生的总人数为多少人,统计表中
的值为多少,统计图中
的值为多少;
(3)求在统计图中,B类所对应扇形圆心角的度数.
(1)30,20%;
(2)150,45,36;
(3)72°
.
(1)观察图表体育类型即可解决问题;
(2)根据“总数=B类型的人数÷
B所占百分比”可得总数;
用总数减去其他类型的人数,可得m的值;
根据百分比=所占人数/总人数可得n的值;
(3)根据圆心角度数=360°
所占百分比,计算即可;
(1)最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
故答案为30,20%.
(2)总人数=30÷
20%=150人,
m=150-12-30-54-9=45,
n%=
×
100%=36%,即n=36,
故答案为150,45,36.
(3)B类所对应扇形圆心角的度数为360°
.
故答案为72°
本题考查统计表、扇形统计图、等知识没解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
58.百日长跑为我校的传统项目,为了解九年级学生的体能状况,从我校九年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
求本次测试共调查了多少名学生?
求本次测试结果为B等级的学生数,并补全条形统计图;
我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少人?
本次测试共调查了50名学生;
本次测试结果为B等级的学生18人,补图见解析;
人.
(1)设本次测试共调查了x名学生,根据总体、个体、百分比之间的关系列出方程即可解决.
(2)用总数减去A、C、D中的人数,即可解决,画出条形图即可.(3)用样本估计总体的思想解决问题.
设本次测试共调查了x名学生.
由题意
,
本次测试共调查了50名学生.
(2)则测试结果为B等级的学生数
(人).
条形统计图如图所示,
本次测试等级为D所占的百分比为
该中学八年级共有900名学生中测试结果为D等级的学生有
人.
本题考查条形图、样本估计总体的思想、扇形统计图等知识,解题的关键是灵活运用这些知识解决问题.
59.某校课外兴趣小组从某市七年级学生中抽取2000人做了如下问卷调查,并将调查结果绘制成如图所示的两幅统计图.
问卷
你平时喝饮料吗?
( )
A.不喝 B.喝
请选择B选项的同学回答下面问题:
请您减少喝饮料的数量,将节省下来的钱捐给希望工程,您愿意平均每月少喝( )
A.0瓶 B.1瓶
C.2瓶 D.2瓶以上
根据上述信息,解答下列问题:
(1)求条形图中n的值.
(2)如果每瓶饮料平均3元钱,“少喝2瓶以上”按少喝3瓶计算:
①这2000名学生一个月少喝饮料能节省多少钱捐给希望工程?
②按上述统计结果估计,该市七年级6万名学生一个月少喝饮料大约能节省多少钱捐给希望工程?
(1)100;
(2)①3420元,②102600元.
(1)根据喝饮料的占60%得出2000×
60%-(445+470+185)=100,即可得出n的值;
(2)①根据(470×
1+185×
2+100×
3)×
3求出节省3420元钱捐给希望工程;
②利用60000×
即可得出七年级6万名学生一个月少喝饮料大约能节省的钱数.
(1)2000×
60%-(445+470+185)=100.
所以条形图中n=100.
(2)①(470×
1+185×
2+100×
3=3420(元).
所以这2000名学生一个月少喝饮料能节省3420元钱捐给希望工程.
②60000×
=102600(元).
所以该市七年级6万名学生一个月少喝饮料大约能节省102600元钱捐给希望工程.
故答案为:
本题主要考查了条形图与扇形图的综合应用,根据已知图形得出正确信息是解题关键.
60.学校开展“阳光体育”活动,学生会为了解学生最喜欢哪一种球类运动项目,
:
足球、
乒乓球、
篮球、
羽毛球,随机抽取了一部分学生进行调查(要求每位同学只能选择一种喜欢的球类),并将调查结果绘制成如下两个不完整的统计图,如图1,图2,请你根据图中提供的信息解答下列问题.
(1)在这次调查中,一共调查了_____名学生;
(2)在图1扇形统计图中,求出“
”部分所对应的圆心角等于_____度;
(3)求喜欢篮球的同学占被抽查人数的百分比,并补全频数分布折线统计图.
(1)100
(2)36(3)20%图略
(1)根据A组有30人,对应的百分比是30%,据此即可求得总人数;
(2)利用总人数减去其它组的人数即可求得D组的人数,然后利用360°
乘以对应的比例即可求得D组对应的扇形的圆心角度数;
(3)把各组的人数在图2中表示出来即可.
(1)调查的总人数是30÷
30%=100(名),
故答案是:
100;
(2)“D”部分的人数是100-30-20-40=10(人),
则所对应的圆心角等于360°
=36°
36;
(3)C项人数为:
100-30-40-10=20人.
补图如下:
本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°