结构动力学例题复习题Word文档格式.docx
《结构动力学例题复习题Word文档格式.docx》由会员分享,可在线阅读,更多相关《结构动力学例题复习题Word文档格式.docx(22页珍藏版)》请在冰豆网上搜索。
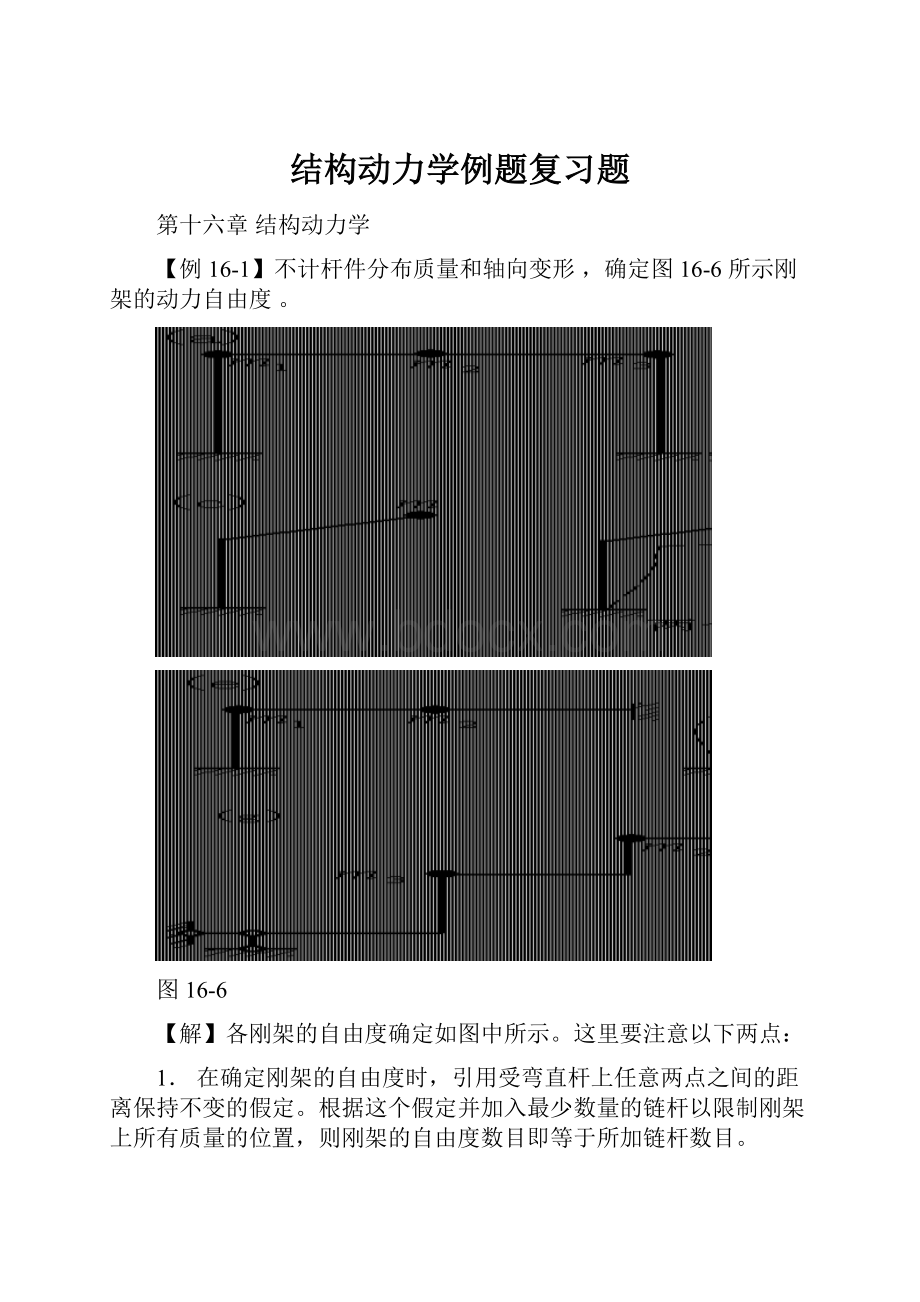
图16-8
3(t);
D点有位移(t)和(t)以顺时针向为正。
则A点有位移(t)和加速度222
33(t)及速度(t);
C点约束反力为Rck(t)。
加速度22
由MB0,有
I13333I2RRCq(t)022224
将惯性力、阻尼力及约束反力代入上式,得
3m333332
(t)][(t)][c(t)][k(t)]q(t)[m0222322224
经整理,运动方程为(t)m99(t)k(t)q(t)c48
小结:
例16-2及例16-3讨论的是单自由度的一般情况下的运动方程的建立。
建立方程的思路是通过分析动力平衡或考虑变形协调。
一般来说,对于单自由度体系,求11和k11的难易程度是相同的,因为它们互为倒数,都可用同一方法求得。
对于多自由度体系,若是静定结构,一般情况下求柔度系数容易些,但对超静定结构就要根据情况而定。
刚度法和柔度法。
它们都是根据达朗贝尔原理和所采用的阻尼理论在体系上加惯性力和阻尼力。
刚度法是考虑质量自由度方向的平衡;
柔度法是建立沿自由度方向位移的协调条件。
所谓结构振动自由度是指:
确定体系全部质点位置所需的独立位移分量的个数。
在例16-3中我们选取(t)为独立位移分量,由此得两质点处的位移、加速度及惯性力的表达式。
体系的振动自由度数目既和体系的质点数目有关,又不完全取决于质点数目,自由度还和体系的可能位移状态有关(如例题16-3),因此要根据具体问题,按自由度定义分析确定。
另一方面,自由度是确定质点空间位置的独立坐标(位移分量)个数,它和结构超静定次数或独立位移个数没有关系。
任何单自由度的振动问题,本质上都可抽象为质点、弹簧、阻尼器体系。
从实际结构到抽象模型的关键是求m和k(或)。
【例16-4】试写出图16-9a质点m的运动微分方程,并计算各系数。
图16-9
【解】
)1PP(t)1QQ(t)y
(1)列位移方程,y11(m
1124a3
(2)计算系数项(图b),11a2aa2EI233EI
(3)计算自由项(图c,d)
1P1112113a11Pa3Pa2aa2Pa2aa/2EI223226a12EI
同理,1Q11Qa312EI
4a3
(4)将系数代入位移方程,3EIymy11a3
12EIP(t)11a3
12EIQ(t)y或m3EI
4a3y11
16P(t)11
16Q(t)
【例16-5】试按刚度法列出图16-10a所示刚架在给定荷载作用下的动力平衡方程。
图16-10
(1)考虑质点m平衡(图b)有
ySI,Im
(2)确定弹性力恢复力S,
弹性力恢复力S可以认为由两部分叠加而成。
第一部分为使m产生位移施加的力R11;
第二部分为m不动在荷载作用下产生的反力R1P,即SR11R1P,
ql3sint3EIR11k11y2y,R1Pala8ala(3)代回动力平衡方程得,
3EIql3sint2myy8alaala【例16-6】图16-11a所示梁不计自重,求自振频率。
图16-11【解】由M图(图b),求得柔度为:
5l/192EI。
所以,31g9EIg2/5Wl3mmg
【例16-7】图16-12a所示单跨梁不计自重,杆无弯曲变形,弹性支座刚度为k,求自振频率。
图16-12
【解】在W处加P1,1/(2k),111/(4k)1gm11mg114kg/W。
42【例16-8】图16-13a所示梁不计自重,W200kN,EI210kNm,求自
振圆频率。
【解】由于对称跨中无转角,求刚度k。
k1
412EI12EI33EI/2,则l32kkg
kg6104kN/m。
k2k1610kN/m54.2s1mmgW200
图16-13
【例16-9】试求图16-14a所示结构的自振频率。
略去杆件自重及阻尼影响。
图16-14
【解】图a为一次超静定结构,用力矩分配法作出单位弯矩图(图b)。
计算质点处的柔度系数11(即位移计算),由图b(或图c)与图d(虚拟状态),得
1l31l12ll31323l3l3
11l0.EI48EI24232EI485121536EIEI
则,
【例16-10】作图16-15a所示结构的动力弯矩幅值图。
已知质点重W=11536EIEI。
8.m1123l3ml3m
2.1kN,扰力幅值P=0.75kN,扰力频率177s-1,梁的抗弯刚度EI=4490kN·
m。
2
图16-15
【解】由图b列幅方程,即
A11m2A1PP,A(111m2)1PP,因为1
m11
A1PP(111m2)12
121PP1PP,1212
由图c求柔度系数11,即114m30.000279m/kN,3EI
11m3
0.000408m/kN,6EI由图d求柔度系数1P,即1P
217856s1,m11
188.63s1,2,,3
1A0.0004080.750.000102m,3
m2A1.37kN
将动荷载P和惯性力mA加于结构上,得动力弯矩幅值图如图e所示。
【例16-11】图16-16a所示体系中,电机重W10kN置于刚性横梁上,电机转速n500r/min,水平方向强迫力为P(t)2kNsin(t),已知柱顶侧移刚度k1.0210kN/m,自振频率100s。
求稳态振动的振幅及最大动力弯矩图。
84-12
图16-16
【解】只有水平振动。
干扰力频率52.36s,动力系数1.378,
静位移yst-1P2kN41.9610m4k1.0210kN/m
4振幅Ayst1.3871.9610m0.27mm
动力弯矩图(图c)MDPM1.37822.756M。
【例16-12】图16-17a所示体系各柱EI=常数,柱高均为l,(18EI/(ml3))。
求最大动力弯矩。
图16-17
【解】由图b可知,k312EI36EI3,则自振频率3llk36EI。
3mml
动力系数12,最大动力弯矩MD(max)P(见图c、d)。
212
【例16-13】求图16-18a所示体系的自振频率和主振型,并作出振型图。
已知:
m12m,m2m,EI=常数。
图16-18
【解】用柔度法作。
1.为求柔度系数,首先绘出单位弯矩图(图b和c)。
由位移计算公式,
111.EI,12210.EI,220.EI
2.求频率
将它们代入频率方程,即
11m1
1212m2
021m11
22m22
展开上式并令1
2得
22
11m122m2112212m1m20
得10
1,211m122m2111m122m2211221221m1m224
两个根为12.883EI,20.366EI从而可得两个自振频率为1110.EIm,21.EIm12
3.求主振型
下面确定相应的两个主振型。
求第一振型时,将1代入上式,由于系数行列式为零,所以两个方程线性相关,只有一个是独立的,可由其中任何一式求得A1值,比如由第一式可得
(1)与A2
(1)的比A12
(1)A1
(1)1m21.3333m11m12210.433812m2
EI
同理可求得第二振型为
(2)A22
(2)A1
两振型的规准化矩阵表达式为111m1224.601212m2
A
(1)111m1m11
(2)1111112,A210.433824.601212m212m2
如图d、e所示。
【例16-14】求图16-19a所示体系的频率方程。
图16-19
【解】本题为两个动力自由度(图b)。
另外注意的是,水平向的振动的质点是2m。
于是由图b列幅值方程:
22112m2x12m2yx2m11112m02,2m2,22m2111212mx22myy
由图c、d求柔度系数,其结果如下。
11l3l34l3,1221,223EI2EI3EI
12EI。
l3【例16-15】求图16-20a所示两个自由度体系的自振频率,k
图16-20
【解】用柔度法解。
首先根据图c、d计算柔度系数,其位移计算公式为
ijijdxc,这里c支座反力为弹支座处位移。
EIk
1112121l3149l3
11llll2llEI23232kEI4k48EI
l319l3l3113l3
22,12216EI4k48EI6EI4k48EI。
1M2E0,解得将它们代入频率方程,
10.EIEI3.,2。
ml3ml3
【例16-16】求图16-21a所示体系的自振频率、振型及广义质量。
图16-21
【解】由图b幅值方程为:
m2l3kA2A10
mA1kA2A1kA102
整理后得,m22kA1kA20kA1m2kA2
令上的系数行列为零,得频率方程,由该方程的两频率如下
2k3k
135
2m,2
22m
振型1:
A1A1(A1,振型2:
1)
22A,见图c。
22
广义质量为:
1
11m01
2
0m21.38m,
1
1m051
2
20m23.62m
1
【例16-17】求图16-22a示桁架的自振频率。
各杆EA为常数。
图16-22
【解】将振动分为竖向、水平分量,求1,2
1127/2EA,224/EA,128/3EA,;
1/2m14197.3.303T/EA,;
11/10.(EA/m),21/20550.(EA/m),
【例16-18】试求图16-23a所示刚架的自振频率和主振型。
EI=常数。
图16-23
【解】图a在不计轴向变形情况下,则与图b的振动是相同的。
因此图a可分成反对称(图c)和正对称(图d)的振动。
第一频率由单自由度频率计算公式
移计算公式,得柔度系数为k可知,则为反对称情况。
由单跨梁的位m
7l3
11768EI
则第一频率为
11768EIEI10.33m117mlml
同理第二频率为
21
m22192EIEI13.33mlml
振型:
第一振为反对称振动,如图e所示;
第二振为对称振动,如图f所示;
【例16-19】图16-24所示梁的质量重G20kN,振动力最大值P4.8kN,干扰频44率30,已知梁的E210GPa,I1.610m。
试求两质点处的最大竖向位移。
梁自重不计。
由图b、c、d计算系数及自由项如下:
112261451P175P,12,1P,2P。
EI3EI8EI24EI
11P并乘以EIMEA30代入,稳态振动位移幅值方程22
有
25.1009A19.514A20.0340
9.514A125.1009A20.038890
解得A12.268103m,A22.409103m
图16-24
【例16-20】图16-25a所示刚架各横梁刚度无穷大,试求各横梁处的位移幅值和柱端
52弯矩幅值。
已知m100t,EI510kN.m。
l5m;
简谐荷载幅值P30kN,每
分钟振动240次。
图16-25
【解】用刚度法解。
稳态振动位移幅值方程K2MAP
有K24EI620
l3231,24EI245105
3396103kN/m。
11
0l5
2
2240
608,2642。
M1001.5(单位t,即103kg)
1
代入稳态振动位移幅值方程,有
449.6691920y10
103192193.25296
y
09632.8352
y330
0
解得
y3
10.0756103m,y20.177110m,y30.5178103m
惯性力幅值为IoM2y,即
I1o2000.07561039.55o6420.177110316.78kNI1502Io0.517810332.711003
本题横梁刚度为无穷大,每层只有两根柱且截面及高度相等,故每根柱的弯矩为MiQih4
Qi为该层的总剪力,等于该层以上水平外力(包括惯性力)的代数和;
h为该层柱高。
于是各层柱端弯矩为32.71540.8875kN.m4
(32.7116.7830)524.3625kN.m中层:
M24
(32.7116.78309.55)536.3kN.m。
如图b所示。
对于横梁的杆端第层:
M14顶层:
M3
弯矩可由刚结点力矩平衡推求。
【例16-21】用振型分解法重作例16-20。
【解】已知频率为:
119.40,241.27,360.67振型为:
A
(1)12.6084.290,A
(2)11.2261.584,TT
TA(3)10.8340.294。
Mm1.5,P1
得广义质量02240Psint8,600
T~M1A
(1)MA
(1)30.607m
~
(2)TM2AMA
(2)6.7637m
T~M3A(3)MA(3)3.1298m
广义荷载
~
(1)TP2.608PsintPA1
~
(2)TP2AP1.226Psint
T~P3A(3)P0.834Psint
因系简谐荷载,又不计阻尼,由下式比较可得
2yyPPsint,则其解为ysintmm(22)
~PT~j2
jjj,这里PjA(j)Psint而Mj
所以
~P2.608P31212sint0.1001310m22M1
(1)30.607m(19.4064)
~P21.266P32sint0.05074710m2222M2
(2)6.763m(41.2764)
~P30.834P33sint0.02621710m2222m(60.6764)M3(3)3.1298
,计算几何坐标yA
110.10013y113即y22.6081.2261.5840.05074710my4.2900.8340.2940.0262173
以下计算同例题16-18,略。
【例16-22】试用能量法求图16-26a所示梁具有均布质量mqg的最低频率,设以梁在自重下的弹性曲线为其振动形式。
图16-26
【解】均布自重(图b)下的弯矩方程(图c)为
ql25qlxqx2
Mx882
有图乘法(图c、d)求挠度曲线方程:
1ql2x2xql25qlxqx2xx2qx2xyxEI82388223382Lq3l2x25lx32x448EI25q2l53523ql3lx5lx2xdx48EI3453.12510EI02234
2q2qydx48EI0llmq222234mydx3lx5lx2xdx2(48EI)00l
mq2
(48EI)2
lmq2l99lx25lx4x30lx20lx12lxdx1.30910(EI)2044268357265l
2qydx0
l
2mydx
0238.7EI15.45EIg,ml4l2q