第五章运筹学 线性规划在管理中的应用案例文档格式.docx
《第五章运筹学 线性规划在管理中的应用案例文档格式.docx》由会员分享,可在线阅读,更多相关《第五章运筹学 线性规划在管理中的应用案例文档格式.docx(32页珍藏版)》请在冰豆网上搜索。
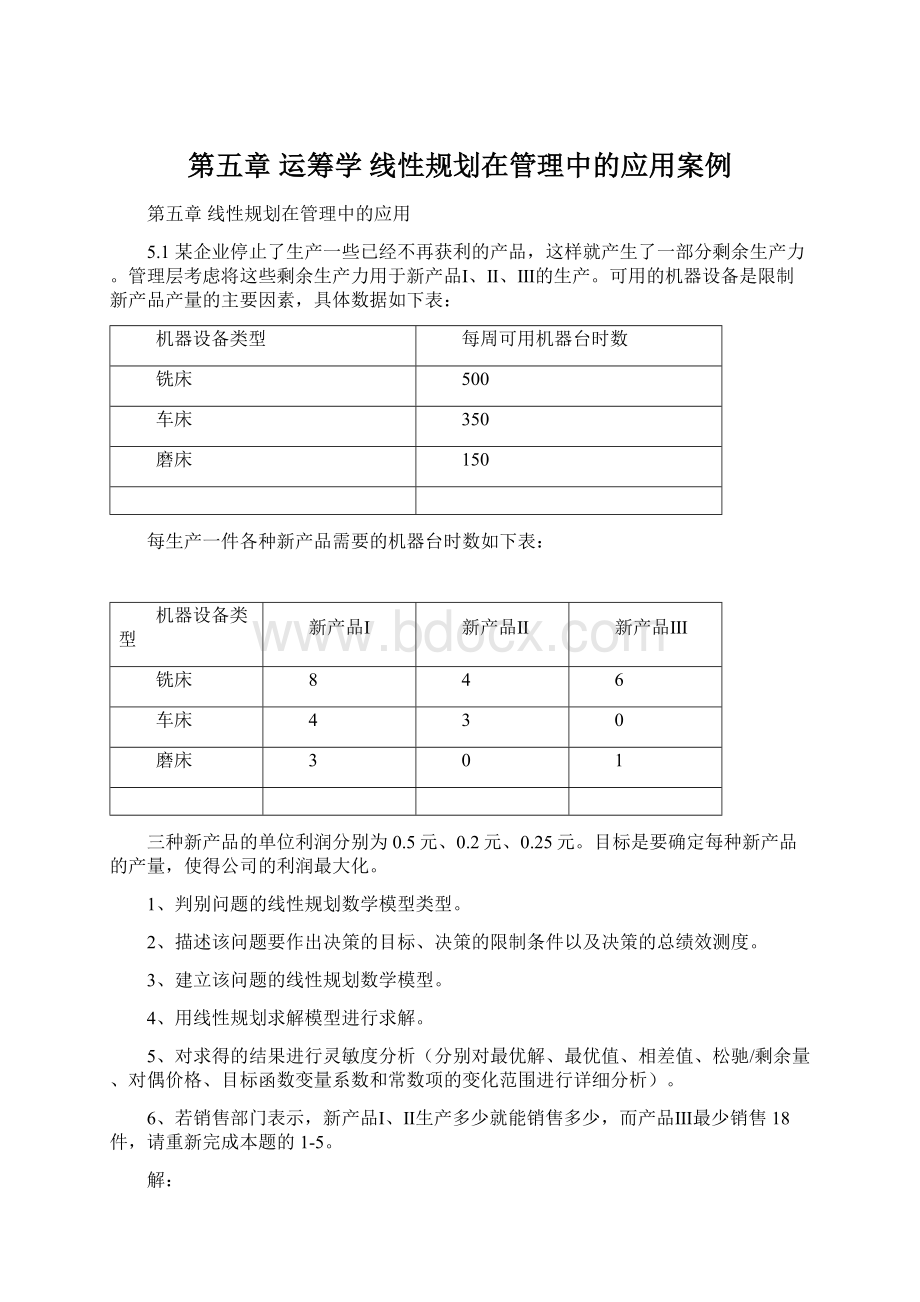
3x1+x3≤150
x1≥0、x2≥0、x3≥0
4、用Excel线性规划求解模板求解结果:
最优解(50,25,0),最优值:
30元。
5、灵敏度分析
目标函数最优值为:
30
变量最优解相差值
x1500
x2250
x30.083
约束松弛/剩余变量对偶价格
10.05
2750
30.033
目标函数系数范围:
变量下限当前值上限
x1.4.5无上限
x2.1.2.25
x3无下限.25.333
常数项数范围:
约束下限当前值上限
1400500600
2275350无上限
337.5150187.5
(1)最优生产方案:
新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。
最大利润值为30元。
(2)x3的相差值是0.083意味着,目前新产品Ⅲ不安排生产,是因为新产品Ⅲ的利润太低,若要使新产品Ⅲ值得生产,需要将当前新产品Ⅲ利润0.25元/件,提高到0.333元/件。
(3)三个约束的松弛/剩余变量0,75,0,表明铣床和磨床的可用工时已经用完,而车床的可用工时还剩余75个工时;
三个对偶价格0.05,0,0.033表明三种机床每增加一个工时可使公司增加的总利润额。
(4)目标函数系数范围
表明新产品Ⅰ的利润在0.4元/件以上,新产品Ⅱ的利润在0.1到0.25之间,新产品Ⅲ的利润在0.333以下,上述的最佳方案不变。
(5)常数项范围
表明铣床的可用条件在400到600工时之间、车铣床的可用条件在275工时以上、磨铣床的可用条件在37.5到187.5工时之间。
各自每增加一个工时对总利润的贡献0.05元,0元,0.033元不变。
6、若产品Ⅲ最少销售18件,修改后的的数学模型是:
maxz=0.5x1+0.2x2+0.25x3
3x1+x3≤150
x3≥18
这是一个混合型的线性规划问题。
代入求解模板得结果如下:
最优解(44,10,18),最优值:
28.5元。
灵敏度报告:
28.5
x1440
x2100
x3180
21440
40-.083
1460500692
2206350无上限
318150165
401830
新产品Ⅰ生产44件、新产品Ⅱ生产10件、新产品Ⅲ生产18件。
最大利润值为28.5元。
(2)因为最优解的三个变量都不为0,所以三个相关值都为0。
(3)四个约束的松弛/剩余变量0,144,0,0,表明铣床和磨床的可用工时已经用完,新产品Ⅲ的产量也刚好达到最低限制18件,而车床的可用工时还剩余144个工时;
四个对偶价格0.05,0,0.033,-0.083表明三种机床每增加一个工时可使公司增加的总利润额,第四个对偶价格-0.083表明新产品Ⅲ的产量最低限再多规定一件,总的利润将减少0.083元。
表明新产品Ⅰ的利润在0.4元/件以上,新产品Ⅱ的利润在0.1到0.25之间,新产品Ⅲ的利润在0.333以下,上述的最佳方案不变。
表明铣床的可用条件在460到692工时之间、车铣床的可用条件在206工时以上、磨铣床的可用条件在18到165工时之间、新产品Ⅲ产量限制在30件以内。
各自每增加一个工时对总利润的贡献0.05元,0元,0.033元,-.083元不变。
5.2某铜厂轧制的薄铜板每卷宽度为100cm,现在要在宽度上进行切割以完成以下订货任务:
32cm的75卷,28cm的50卷,22cm的110卷,其长度都是一样的。
问应如何切割可使所用的原铜板为最少?
本问题是一个套材下料问题,用穷举法找到所有可能切割的方式并建立数学模型:
minf=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10
S.T.3x1+2x2+2x3+x4+x5+x6≥75
x2+2x4+x6+3x7+2x8+x9≥50
x3+3x5+x6+2x8+3x9+4x10≥110
xi≥0(i=1,2…..10)
用Excel线性规划求解模型板求解:
最优解:
(18.33,0,0,0,20,0,0.25,0,0,0),最优值:
63.3333
因为铜板切割时必须整卷切割所以需要做整数近似。
即其结果为:
即最优解:
(19,0,0,0,20,0,0.25,0,0,0),最优值:
64
灵敏度分析报告:
63.333
x118.3330
x20.056
x30.111
x40.111
x5200
x60.167
x70.167
x8250
x90.056
x100.111
10-.333
20-.278
30-.222
x1.7511.071
x2.9441无上限
x3.8891无上限
x4.8891无上限
x5.83311.083
x6.8331无上限
x7.8331无上限
x8.44411.111
x9.9441无上限
x10.8891无上限
12075无上限
2050110
350110275
这是一个统计型的线性规划问题,所以分析价值系数的取值范围和相差都没有意义。
松弛/剩余变量都为0,表示最优方案已达到三种规格薄铜板数量的最低限。
三个约束条件的对偶价格-.333、-.278、-.222分别表示三种规格薄铜板数量的最低限再增加一个,将增加原铜板.333cm、.278cm、.222cm。
这个数字实际跟薄铜板长度规格相一致。
常数项数范围表示三种规格薄铜板数量的最低限在这些范围内,每增一个限额所原原铜板.333cm、.278cm、.222cm不变。
这里需要特别指出的是,第一种规格的薄铜板32cm宽,已使三块组合就能比较恰当地用完原铜板,所以这种规格的薄铜板无论增加多少,都不改变用原铜板的比例。
5.3某医院对医生工作的安排为4小时一个工作班次,每人要连续工作二个班次。
各班次需要医生人数如下表:
班次
时间
人数
0:
00-4:
00
2
4:
00-8:
7
8:
00-12:
9
12:
00-16:
12
5
16:
00-20:
20:
00-24:
其中,第6班报到的医生要连续上班到第二天的第1班。
问在各班开始时应该分别有几位医生报到。
若参加1、2、6班的医生需要支付夜班津贴,为了使支付总的夜班津贴为最少,应如何安排各班开始时医生的报到人数。
第一步:
不考虑夜班津贴。
线性规划数学模型为:
minf=x1+x2+x3+x4+x5+x6
S.T.x6+x1≥4
x1+x2≥7
x2+x3≥9
x3+x4≥12
x4+x5≥8
x5+x6≥6
xi≥0(i=1,2,3,4,5,6)
用Excel线性规划求解模板求解得:
第一班安排7人,第三班安排10人,第四班安排2人,第五班安排6人,第二、第六班不安排人。
总人数为25人。
25
x170
x200
x3100
x420
x560
x600
13.0
20-1
31.0
40--1
50.0
60--1
x10.11
x211无上限.
x30.11
x41.12
x5011
x611无上限
1无下限47
247无上限
3无下限910
41112无上限
5689
6568
这是一统计型线性规划规划问题,所以相差值的价值系数的变化范围没有必要分析。
所需人数
本段安排人数
上段安排人数
本段实际人数
多余人数
10
合计
46
25
50
松弛/剩余变量一栏就是上表的“多余人数”一列是各时间段安排所剩余的人数。
“对偶价格”一栏。
第一个常数项由4增加到5,因为还剩下2人,所以不会改变最优值;
第二个常数项由7增加到8,因为再没有剩余的人,所以本班必须再多安排一个人最优值解也必须增加1,因为是求最小化问题,所以对偶价格为-1;
第三个常数项由9增加到10,刚好将原来剩余的人用上,所以不会改变最优值;
第四个、第六个常数项与第二个常数项一样;
第五个常数项由2增加到3,因为再没有剩余的人,所以本班必须再多安排一个人,但下个班就可以再少安排一个人,所以不会改变最优值;
本题的这种情况是每一个变量都会影响到两个时段的结果,所以在进行灵敏度分析时也必定要考虑这个因素,这里第一个时段是特殊情况(有资源剩余),其余的时段分析时相邻两个是相互影响的。
因此,第2时段为-1,第3时段为0,后面的依次相反。
若第2时段为0,则第3时段就为-1。
第二步:
考虑夜班津贴。
minf=x1+x2+x3+x5+x6
即:
总人数还是25人,但每班安排人数有所调整:
第一班不安排人,第二班安排7人,第三班安排2人,第四班安排10人,第五班安排0人,第六班安排6人。
15
x101
x270
x320
x4100
x500
x660
120
200
30-1
400
520
60-1
x101无上限
x2112
x3011
x4001
x511无上限
x6011
1无下限46
2579
37911
41012无上限
5无下限810
646无上限
这是一统计型线性规划规划问题,所以相差值的价值系数的变化范围没有必要分析。
第二个常数项由7增加到8,由于上段时间已增一个人,这个人本班还上班,所以本也不需要增加人。
第三个常数项由9增加到10,前面安排的人都已下班,本班刚好只朋9人,若需求再增加一人,就需要新安排一人所以对偶价格-1;
第四个、第五个、第六个常数项与前三个常数项一样;
5.4某塑料厂要用四种化学配料生产一种塑料产品,这四种配料分别由A、B、C三种化学原料配制,三种化学原料的配方及原料价格如下表:
配料
价格(元/公斤)
含原料A(%)
30
40
20
15
11
含原料B(%)
60
13
含原料C(%)
要配制的塑料产品中,要求含有20%的原料A,不少于30%的材料B和不少于20%的原料C。
由于技术原因,配料1的用量不能超过30%,配料2的用量不能少于40%。
第一次配制的塑料产品不能少于5公斤。
请设计一套配料方案,使总的成本为最低。
线性规划数学模型:
minf=10.7x1+11.3x2+11.8x3+9.45x4
S.T.0.1x1+0.2x2-0.05x4=0
-0.1x1+0.3x3+0.1x4≥0
0.2x1+0.05x2-0.05x3+0.1x4≥0
0.7x1-0.3x2-0.3x3-0.3x4≥0
-0.4x1+0.6x2-0.4x3-0.4x4≤0
x1+x2+x3+x4≥5
xi≥0(i=1,2,3,4,)
将模型代入到线性规划求解模板,得结果:
用配料1,1.5公斤;
用配料2,0.1公斤;
用配料3,0公斤;
用配料4,3.4公斤;
花费总的最低成本49.31元。
49.31
x11.50
x2.10
x301.98
x43.40
10-7.4
2.190
3.6450
40-.14
51.90
60-9.862
x110.5610.7无上限
x2-481.811.311.533
x39.8211.8无上限
x4-5.0539.459.8
1-.0250.475
2无下限0.19
3无下限0.645
4-1.50.167
5-1.90无上限
605无上限
本问题的相差值栏,x3的相差值为1.98,表示目前配料3的成本11.8太高,无法选用,若该配料的成本再降低1.98元就可以选取用。
松弛/剩余变量栏:
前五个给条件都表示的是配料或原料的配比关系。
松弛/剩余变量为0关系表示已完全按要求配比,不为0的表示没有达到配比要求。
第五个约束是总产品的产量最低限,松弛/剩余变量为0表示已达到产量要求。
关五个约束的对偶价格表示配料或者说原料不匹配时,对总费用的影响。
不为0的对偶价格表示配比每差一个单位都会使总费用的增加量。
第五个对偶价格是每增加一公斤的产品,需要增加的费用值。
在学数项取值范围栏:
前五个约束在常数项在这个范围内,保持上述的对偶价格,而此时的上限都不高,说明这个最优方案中的匹配关系失衡并不严重,若比例失衡将会导致费用的增加比例更大。
对五个对偶价格实际上说明了该产品的绝对成本,在这个方案下,生产多少的产品都是这个成本构成。
5.5某工厂生产Ⅰ、Ⅱ、Ⅲ、Ⅳ四种产品,产品Ⅰ需经过A、B两种机器加工,产品Ⅱ需经过A、C两种机器加工,产品Ⅲ需经过B、C两种机器加工,产品Ⅳ需经过A、B两种机器加工。
有关数据见下表所示:
产品
机器生产率(件/小时)
原料成本(元/件)
产品价格(元/件)
A
B
C
Ⅰ
16
65
Ⅱ
80
Ⅲ
Ⅳ
18
70
机器成本(元/小时)
200
225
每周可用机时数
120
请为该厂制定一个最优生产计划。
maxZ=21.5x1+22.5x2+8x3+27x4
S.T.2x1+x2+x4≤3000
x1+2x3+2x4≤2400
3x2+4x3≤4200
xi≥0(i=1,2,......4)
最优生产方案:
产品Ⅰ生产267件;
产品Ⅱ生产1400件;
产品Ⅲ不安排生产;
产品Ⅳ生产1067件。
可获得的最高利润:
66033.3元。
66033.3495
-----------------------
x1266.6670
x214000
x3030.8333
x41066.6670
----------------------------
105.333
2010.833
305.722
-------------------------------
x113.521.545
x25.33322.5无上限
x3无下限838.333
x410.752743
1260030006200
280024003200
3042005400
此模型的最优解中,四个变量有三个变量不为0,即需要安排生产,另一个为0的变量表示产品Ⅲ由于成本高或价格低,使所获的利润太低,不值得生产。
从相差值栏可见,该产品的单位利润需要再增加30.8333元才值得生产。
松弛/剩余变量栏中三个数据都为0,表示该决策中所提供三种设备的机时都已全部利用,没有剩余;
从对偶价格栏还可以看到三种设备的机时虽然都已用尽,但此时对三种设备增加机时,则设备B所带来的总利润为最多。
因此设备B是瓶径。
从约束条件的取值范围也可以看到这一点,因为设备B的机时取值范围最小,因此该设备是关键。
5.6某企业生产Ⅰ、Ⅱ两种产品,市场两种产品的需求量为:
产品Ⅰ在1-4月份每月需1万件,5-9月份每月需3万件,10-12月份每月需10万件;
产品Ⅱ在3-9月份每月需1.5万件,其他月份每月需5万件。
该企业生产这两种产品的成本为:
产品Ⅰ在1-5月份生产时每件5元,6-12月份生产时每件4.5元;
产品Ⅱ在1-5月份生产时每件8元,6-12月份生产时每件7元;
该企业每月生产两种产品的能力总和不超过12万件。
产品Ⅰ容积为每件0.2立方米,产品Ⅱ容积为每件0.4立方米。
该企业仓库容积为1.5万立方米。
要求:
1、问该企业应如何安排生产,使总的生产加工储存费用为最少,建立线性规划数学模型并求解,若无解请说明原因。
2、若该企业的仓库容积不足时,可从外厂租借。
若占用本企业的仓库每月每立方米需1万元的储存费,而租用外厂仓库时其储存费用为每月每立方米1.5万元,试问在满足市场需求情况下,该企业又应如何安排生产,使总的生产加储存费用为最少。
1、这是一个72个变量、60个约束条件的线性规划问题,若不考虑外厂租借仓库,则无法求解(无解),只有考虑外厂租借仓库才能解决本问题。
分析及解决过程和结果可见下表:
月份
仓容
外存
产
品
销售量(千件)
100
15000(m3)
1元/m3
容量
不限
1.5元/m3
成本(元、件)
4.5
产量(件)
x1=10
x2=10
x3=10
x4=10
x5=30
x6=30
x7=30
x8=45
x9=105
x10=70
x11=70
x12=70
总容积(千m3)
0.2x1
0.2x2