高考数学人教版一轮复习练习第二章 第9节 函数与数学模型Word文件下载.docx

高考数学人教版一轮复习练习第二章 第9节 函数与数学模型Word文件下载.docx

《高考数学人教版一轮复习练习第二章 第9节 函数与数学模型Word文件下载.docx》由会员分享，可在线阅读，更多相关《高考数学人教版一轮复习练习第二章 第9节 函数与数学模型Word文件下载.docx（11页珍藏版）》请在冰豆网上搜索。

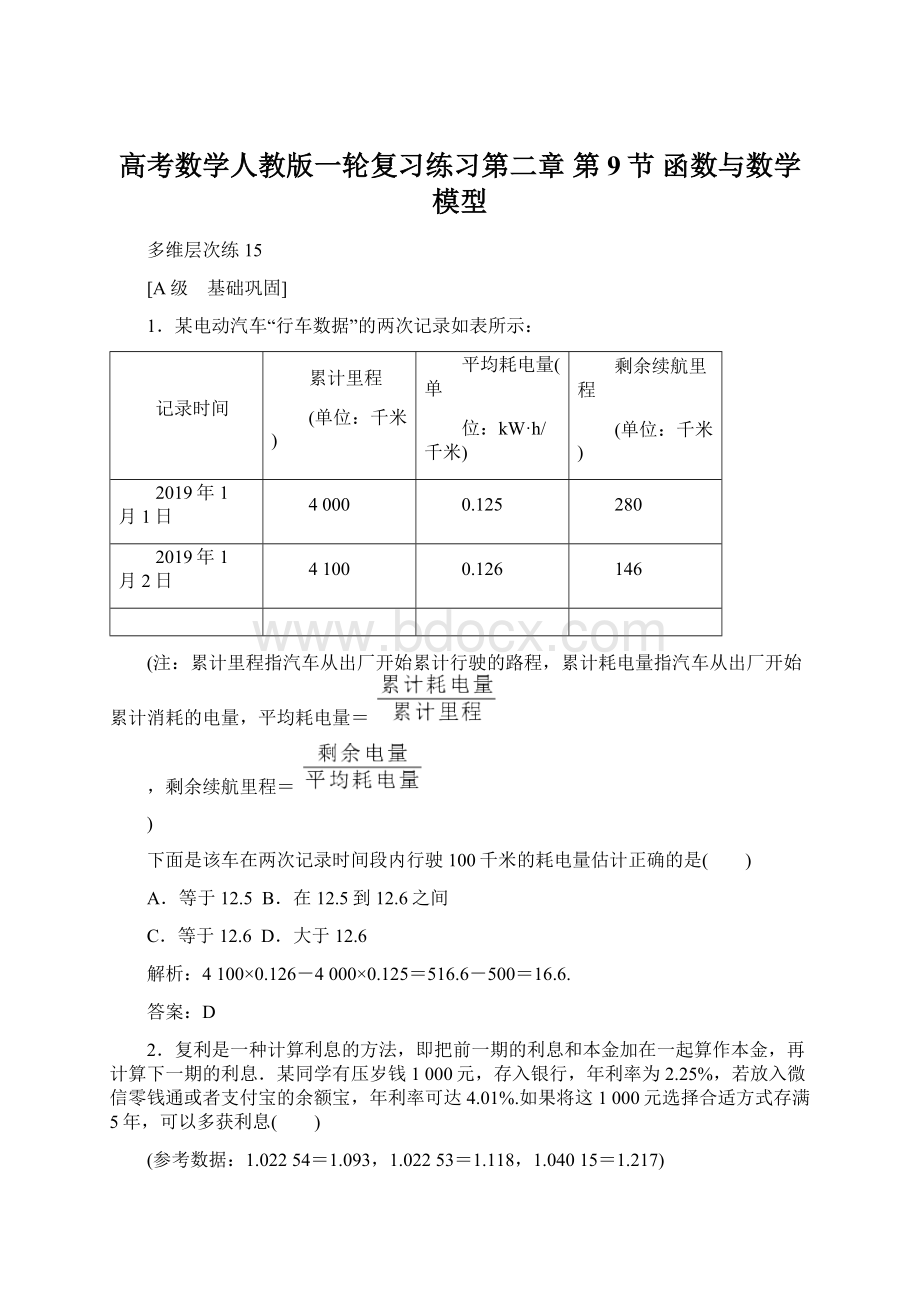
（注：

累计里程指汽车从出厂开始累计行驶的路程，累计耗电量指汽车从出厂开始累计消耗的电量，平均耗电量＝

，剩余续航里程＝

）

下面是该车在两次记录时间段内行驶100千米的耗电量估计正确的是（　　）

A．等于12.5B．在12.5到12.6之间

C．等于12.6D．大于12.6

解析：

4100×

0.126－4000×

0.125＝516.6－500＝16.6.

答案：

D

2．复利是一种计算利息的方法，即把前一期的利息和本金加在一起算作本金，再计算下一期的利息．某同学有压岁钱1000元，存入银行，年利率为2.25%，若放入微信零钱通或者支付宝的余额宝，年利率可达4.01%.如果将这1000元选择合适方式存满5年，可以多获利息（　　）

（参考数据：

1.02254＝1.093，1.02253＝1.118，1.04015＝1.217）

A．176元B．104.5元C．77元D．88元

将1000元钱存入微信零钱通或者支付宝的余额宝，选择复利的计算方法，则存满5年后的本息和为1000×

1.04015＝1217元，故共得利息1217－1000＝217元．将1000元存入银行，不选择复利的计算方法，则存满5年后的利息为1000×

0.0225×

5＝112.5元，故可以多获利息217－112.5＝104.5（元）．

B

3．汽车的“燃油效率”是指汽车每消耗1L汽油行驶的里程．下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是（　　）

A．消耗1L汽油，乙车最多可行驶5km

B．以相同速度行驶相同路程，三辆车中，甲车消耗汽油量最多

C．甲车以80千米/小时的速度行驶1小时，消耗10升汽油

D．某城市机动车最高限速80千米/小时，相同条件下，在该市用丙车比用乙车更省油

根据图象知消耗1L汽油，乙车最多行驶里程大于5km，故选项A错；

以相同速度行驶时，甲车燃油效率最高，因此以相同速度行驶相同路程时，甲车消耗汽油最少，故选项B错；

甲车以80km/h的速度行驶时燃油效率为10km/L，行驶1h，里程为80km，消耗8L汽油，故选项C错；

最高限速80km/h，丙车的燃油效率比乙车高，因此相同条件下，在该市用丙车比用乙车更省油，选项D正确．

4．（2017·

北京卷）根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080，则下列各数中与

最接近的是（参考数据：

lg3≈0.48）（　　）

A．1033B．1053C．1073D．1093

M≈3361，N≈1080，

≈

，

则lg

≈lg

＝lg3361－lg1080＝361lg3－80lg10≈93.

所以

≈1093.

5．某位股民购进某支股票，在接下来的交易时间内，他的这支股票先经历了n次涨停（每次上涨10%），又经历了n次跌停（每次下跌10%），则该股民这支股票的盈亏情况（不考虑其他费用）为（　　）

A．略有盈利

B．略有亏损

C．没有盈利也没有亏损

D．无法判断盈亏情况

设该股民购进这支股票的价格为a元，则经历n次涨停后的价格为a（1＋10%）n＝a×

1.1n元，经历n次跌停后的价格为a×

1.1n×

（1－10%）n＝a×

0.9n＝a×

（1.1×

0.9）n＝0.99n·

a<

a，故该股民这支股票略有亏损．

6．我们处在一个有声世界里，不同场合，人们对声音的音量会有不同要求．衡量音量大小的单位是分贝（dB），对于一个强度为I的声波，其音量的大小η可由如下公式计算：

η＝10lg

（其中I0是人耳能听到声音的最低声波强度），则70dB的声音的声波强度I1是60dB的声音的声波强度I2的（　　）

A.

倍B．10

倍

C．10倍D．ln

由η＝10lg

得I＝I010

，所以I1＝I0107，I2＝I0106，所以

＝10，所以70dB的声音的声波强度I1是60dB的声音的声波强度I2的10倍．

C

7．“好酒也怕巷子深”，许多著名品牌是通过广告宣传进入消费者视线的．已知某品牌商品广告销售的收入R与广告费A之间满足关系R＝a

（a为常数），广告效应为D＝a

－A.那么精明的商人为了取得最大广告效应，投入的广告费应为________（用常数a表示）．

令t＝

（t≥0），则A＝t2，所以D＝at－t2＝－

＋

a2.所以当t＝

a，即A＝

a2时，D取得最大值．

a2

8．（2018·

浙江卷）我国古代数学著作《张邱建算经》中记载百鸡问题：

“今有鸡翁一，值钱五；

鸡母一，值钱三；

鸡雏三，值钱一．凡百钱，买鸡百只，问鸡翁、母、雏各几何？

”设鸡翁，鸡母，鸡雏个数分别为x，y，z，则

当z＝81时，x＝____________，y＝____________．

法一　由题意，得

即

解得

法二　100－81＝19（只），

81÷

3＝27（元），

100－27＝73（元）．

假设剩余的19只鸡全是鸡翁，则5×

19＝95（元）．

因为95－73＝22（元），

所以鸡母：

22÷

（5－3）＝11（只），

鸡翁：

19－11＝8（只）．

8　11

9．某种病毒经30分钟繁殖为原来的2倍，且知病毒的繁殖规律为y＝ekt（其中k为常数，t表示时间，单位：

小时，y表示病毒个数），则k＝________，经过5小时，1个病毒能繁殖为________个．

当t＝0.5时，y＝2，所以2＝e

k，

所以k＝2ln2，所以y＝e2tln2，

当t＝5时，y＝e10ln2＝210＝1024.

2ln2　1024

10．候鸟每年都要随季节的变化而进行大规模的迁徙，研究某种鸟类的专家发现，该种鸟类的飞行速度v（单位：

m/s）与其耗氧量Q之间的关系为v＝a＋blog3

（其中a，b是实数）．据统计，该种鸟类在静止时其耗氧量为30个单位，而飞行速度为1m/s时其耗氧量为90个单位．

（1）求出a，b的值；

（2）若这种鸟类为赶路程，飞行的速度不能低于2m/s，则其耗氧量至少要多少个单位？

解：

（1）由题意可知，当这种鸟类静止时，它的速度为0m/s，此时耗氧量为30个单位，故有a＋blog3

＝0，

即a＋b＝0；

当耗氧量为90个单位时，速度为1m/s，故有a＋blog3

＝1，

整理得a＋2b＝1.

解方程组

得

（2）由

（1）知，v＝－1＋log3

.

所以要使飞行速度不低于2m/s，则有v≥2，

即－1＋log3

≥2，即log3

≥3，解得Q≥270.

所以若这种鸟类为赶路程，飞行的速度不能低于2m/s，

则其耗氧量至少要270个单位．

[B级　能力提升]

11.（多选题）如图，某湖泊的蓝藻的面积y（单位：

m2）与时间t（单位：

月）的关系满足y＝at，则下列说法正确的是（　　）

A．蓝藻面积每个月的增长率为100%

B．蓝藻每个月增加的面积都相等

C．第6个月时，蓝藻面积就会超过60m2

D．若蓝藻面积蔓延到2m2，3m2，6m2所经过的时间分别是t1，t2，t3，则一定有t1＋t2＝t3

由点（1，2）在y＝at图象上，

所以a＝2，则y＝2t，

因此蓝藻每个月增长面积Δy＝2t＋1－2t＝2t，B错误．

所以蓝藻面积每个月增长率是

＝1＝100%，A正确．

当t＝6时，y＝26＝64>

60，C正确．

又2t1＝2，2t2＝3，2t3＝6，

所以2t1·

2t2＝2t3，则t1＋t2＝t3，D项正确．

ACD

12．物体在常温下的温度变化可以用牛顿冷却规律来描述：

设物体的初始温度是T0，经过一定时间t（单位：

min）后的温度是T，则T－Ta＝（T0－Ta）

，其中Ta称为环境温度，h称为半衰期．现有一杯用85℃热水冲的速溶咖啡，放在21℃的房间中，如果咖啡降到37℃需要16min，那么这杯咖啡要从37℃降到29℃，还需要________min.

由题意知Ta＝21℃.

令T0＝85℃，T＝37℃，

得37－21＝（85－21）·

，所以h＝8.

令T0＝37℃，T＝29℃，

则29－21＝（37－21）·

，所以t＝8.

8

13.某禁毒机构测定，某种毒品服用后每毫升血液中的含毒量y（微克）与时间t（小时）之间近似满足如图所示的曲线．

（1）写出服用毒品后y与t之间的函数解析式；

（2）据进一步测定，每毫升血液中含毒量不少于0.50微克时会有重度躁动状态，求服用毒品后重度躁动状态的持续时间．

（1）由题中图象，设y＝

当t＝1时，由y＝4，得k＝4；

由

＝4，得a＝3.所以y＝

（2）由y≥0.50，得

或

≤t≤4，因此服用毒品后重度躁动状态持续4－

＝

（小时）．

[C级　素养升华]

14．甲、乙、丙、丁四个物体同时从某一点出发向同一方向运动，它们的路程fi（x）（i＝1，2，3，4）关于时间x（x≥0）的函数解析式分别为f1（x）＝2x－1，f2（x）＝x2，f3（x）＝x，f4（x）＝log2（x＋1），有以下结论：

①当x>

1时，甲走在最前面；

②当x>

1时，乙走在最前面；

③当0<

x<

1时，丁走在最前面，当x>

1时，丁走在最后面；

④如果它们一直运动下去，最终走在最前面的是甲．

其中正确结论的序号为________．

甲、乙、丙、丁的路程fi（x）（i＝1，2，3，4）关于时间x（x≥0）的函数解析式分别为f1（x）＝2x－1，f2（x）＝x2，f3（x）＝x，f4（x）＝log2（x＋1）．它们对应的函数模型分别为指数型函数模型、二次函数模型的、一次函数模型、对数型函数模型．

当x＝2时，f1

（2）＝3，f2

（2）＝4，所以①不正确．

当x＝5时，f1（5）＝31，f2（5）＝25，所以②不正确．

根据四种函数的变化特点，对数型函数的增长速度是先快后慢，又当x＝1时，甲、乙、丙、丁四个物体走过的路程相等，从而可知．当0<

1时，丁走在最后面，所以③正确．

指数型函数的增长速度是先慢后快，当运动的时间足够长时，最前面的物体一定是按照指数型函数模型运动的物体，即一定是甲物体，所以④正确．

③④