八年级数学竞赛例题专题讲解22关于中点的联想Word格式文档下载.docx

八年级数学竞赛例题专题讲解22关于中点的联想Word格式文档下载.docx

《八年级数学竞赛例题专题讲解22关于中点的联想Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《八年级数学竞赛例题专题讲解22关于中点的联想Word格式文档下载.docx（13页珍藏版）》请在冰豆网上搜索。

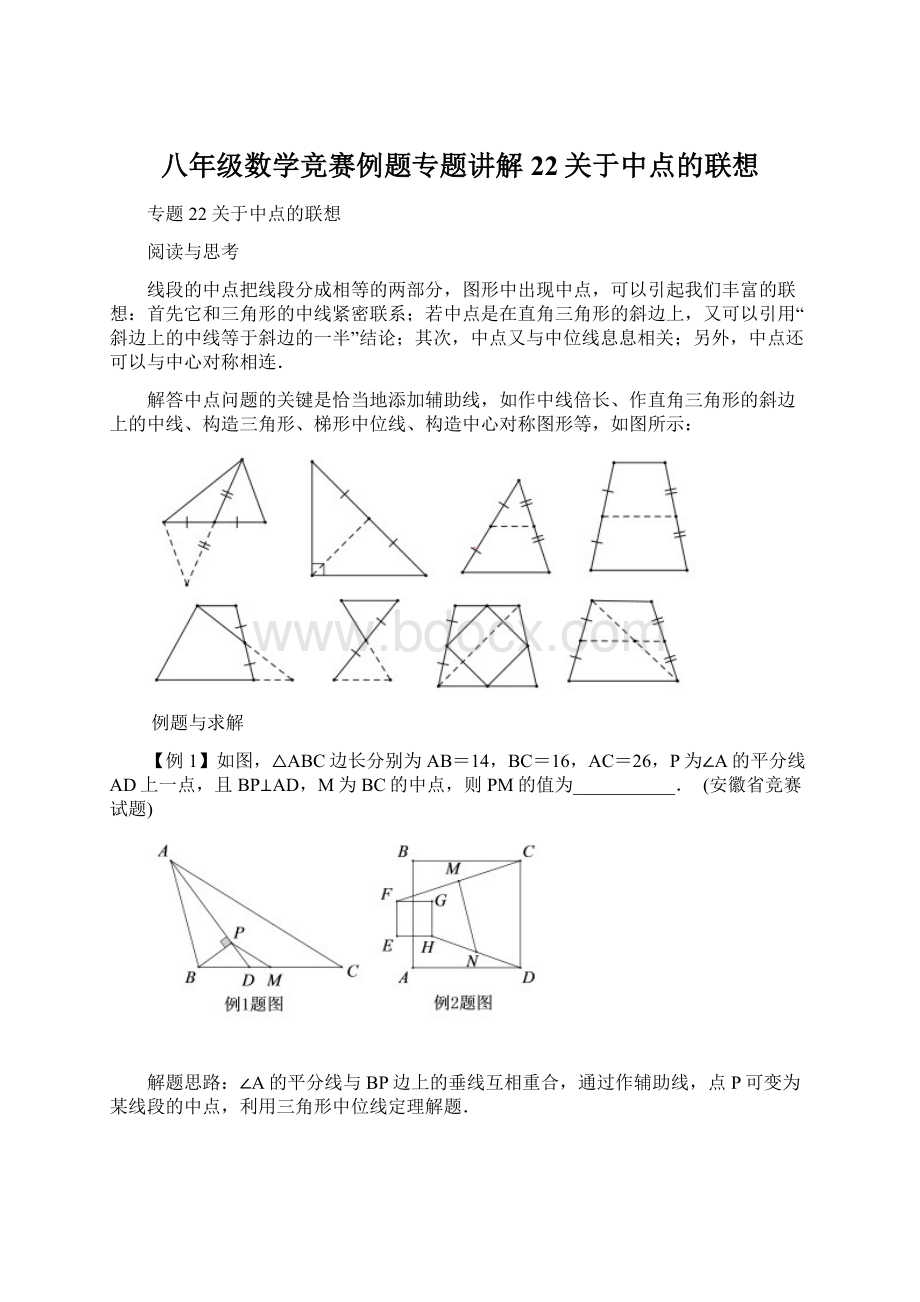
∠A的平分线与BP边上的垂线互相重合，通过作辅助线，点P可变为某线段的中点，利用三角形中位线定理解题．

【例2】如图，边长为1的正方形EFGH在边长为3的正方形ABCD所在的平面上移动，始终保持EF∥AB，线段CF，DH的中点分别为M，N，则线段MN的长度为（）（北京市竞赛试题）

A．

B．

C．

D．

连接CG，取CG的中点T，构造三角形中位线、梯形中位线．

【例3】如图，在△ABC中，AB＝AC，延长AB到D，使BD＝AB，E为AB中点，连接CE，CD，

求证：

CD＝2EC．（宁波市竞赛试题）

图形中有两个中点E，B，联想到与中点相关的丰富知识，将线段倍分关系的证明转化为线段相等关系的证明，关键是恰当添加辅助线．

【例4】如图1，P是线段AB上一点，在AB的同侧作△APC和△BPD，使∠APC＝∠BPD，PC＝PA，PD＝PB，连接CD，点E，F，G，H分别是AC，AB，BD，CD的中点，顺次连接E，F，G，H．

（1）猜想四边形EFGH的形状，直接回答，不必说明理由；

（2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，

（1）中的结论还成立吗？

说明理由；

（3）如果

（2）中，∠APC＝∠BPD＝90°

，其他条件不变，先补全图3，再判断四边形EFGH的形状，并说明理由．（营口市中考试题）

图①图②图③

结论随着条件的改变也许发生变化，但解决问题的方法是一致的，即通过连线，为三角形中位线定理的应用创造条件．

【例5】如图，以△ABC的AB，AC边为斜边向形外作直角三角形ABD和ACE，且使∠ABD＝∠ACE，M是BC的中点，求证：

DM＝EM．（“祖冲之杯”邀请赛试题）

显然△DBM不全等于△ECM，必须通过作辅助线，构造全等三角形证明DM＝EM．

【例6】如图，已知△ABC中，∠ACB＝90°

，AB边上的高CH与△ABC的两条内角平分线AM，BN分别交于P，Q两点，PM，QN的中点分别为E，F，求证：

EF∥AB．（全国初中数学联赛题）

从图形的形成过程，逐步探索相应结论．将原问题分解为多个小问题．

A级

1．如图，若E，F，G，H分别是四边形ABCD各边的中点，则四边形EFGH是____________．

（1）如果把条件中的四边形ABCD依次改为矩形、菱形、正方形或等腰梯形，其他条件不变，那么所得的四边形EFGH分别为_______________________；

（2）如果把结论中的平行四边形EFGH依次改为矩形、菱形、正方形，那么原四边形ABCD应具备的条件是_______________________．（湖北省黄冈市中考试题）

2．如图，已知AG⊥BD，AF⊥CE，BD，CE分别是∠ABC和∠ACB的角平分线，若BF＝2，ED＝3，GC＝4，则△ABC的周长为_______________．（重庆市竞赛试题）

3．如图，在△ABC中，AB＝AC，AD⊥BC于点D，E是AC的中点，若BC＝16，DE＝5，则AD＝______________．（南京市中考试题）

4．如图，在△ABC中，AB＝AC，M，N分别是AB，AC的中点，D，E为BC上的点，连接DN，EM，若AB＝13cm，BC＝10cm，DE＝5cm，则图中阴影部分的面积为________________．

（北京市中考试题）

5．A′，B′，C′，D′顺次为四边形ABCD的各边的中点，下面条件中使四边形A′B′C′D′为正方形的条件是（）

A．四边形ABCD是矩形B．四边形ABCD是菱形

C．四边形ABCD是等腰梯形D．四边形ABCD中，AC⊥BD且AC＝BD

6．若等腰梯形的两条对角线互相垂直，中位线长为8cm，则该等腰梯形的面积为（）

A．16cm2B．32cm2C．64cm2D．112cm2

7．如图，梯形ABCD中，AD∥BC，E，F分别是BD，AC的中点，若AD＝6cm，BC＝18cm，则EF的长为（）

A．8cmB．7cmC．6cmD．5cm

8．如图，在梯形ABCD中，AD∥EF∥GH∥BC，AE＝EG＝GB，AD＝18，BC＝32，则EF＋GH＝（）

A．40B．48C．50D．56（泰州市中考试题）

第8题图第9题图

9．如图，在△ABC中，∠B＝2∠C，AD⊥BC于点D，M是BC的中点，求证：

DM＝

AB．

10．如图，在△ABC中，BD＝CE，BE，CD的中点分别是M，N，直线MN分别交AB，AC于点P，Q，求证：

AP＝AQ．

11．在图1至图3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．

（1）如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：

FM=MH，FM⊥MH；

（2）将图1中的CE绕点C顺时针旋转一个锐角，得到图2，求证：

△FMH是等腰直角三角形；

（3）将图2中的CE缩短到图3的情况，△FMH还是等腰直角三角形吗？

（不必说明理由）

（2009年河北省中考试题）

12．在六边形ABCDEF中，AB∥DE，BC∥EF，CD∥FA，AB＋DE＝BC＋EF，A1，B1，D1，E1分别是边AB，BC，DE，EF的中点，A1D1＝B1E1．求证：

∠CDE＝∠AFE．

B级

1．如图，正方形ABCD两条对角线相交于点E，∠CAD的平分线AF交DE于点G，交DC于点F，若GE＝24，则FC＝_________________．

2．如图，四边形ABCD的对角线AC，BD相交于点F，M，N分别是AB，CD的中点，MN分别交BD，AC于点P，Q，且∠FPQ＝∠FQP，BD＝10，则AC＝_________．（重庆市竞赛试题）

3．如图，在△ABC中，∠BAC＝120°

，以AB，AC为边分别向形外作正三角形ABD和正三角形ACE，M为AD的中点，N为AE的中点，P为BC的中点，则∠MPN＝_________．（北京市竞赛试题）

4．如图，已知A为DE的中点，设△DBC，△ABC，△EBC的面积分别为S1，S2，S3，则S1，S2，S3之间的关系是（）

A．S2＝

（S1＋S3）B．S2＝

（S3―S1）C．S2＝

（S1＋S3）D．S2＝

（S3―S1）

5．如图，在图形ABCD中，AB∥DC，M为DC的中点，N为AB的中点，则（）

A．MN＞

（AD＋BC）B．MN＜

（AD＋BC）

C．MN＝

（AD＋BC）D．无法确定MN与

（AD＋BC）的关系

6．如图，凸四边形ABCD的面积是a，E，F，G，H分别是AB，BC，CD，DA的中点，那么图中的阴影部分的面积为（）

A．

aB．

aC．

aD．

a

（江苏省竞赛试题）

7．如图，在△ABC中，D为AB的中点，分别延长CA，CB到点E，F，使DE＝DF，过E，F分别作CA，CB的垂线，相交于点P．求证：

∠PAE＝∠PBF．（全国初中数学联赛试题）

8．如图，锐角△ABC中，作高BD和CE，过顶点B，C分别作DE的垂线BF和CG，求证：

EF＝DG．

（全俄奥林匹克数学竞赛试题）

9．如图，在△ABC中，AD是BC边上的中线，点M在AB边上，点N在AC边上，并且∠MDN＝90°

，如果BM2＋CN2＝DM2＋DN2．求证：

AD2＝

（AB2＋AC2）．（北京市竞赛试题）

10．已知：

△ABD和△ACE都是直角三角形，且∠ABD＝∠ACE＝90°

．如图1，连接DE，设M为DE的中点．

（1）求证：

MB＝MC；

（2）设∠BAD＝∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图2的位置，试问：

MB＝MC是否还成立?

请说明理由．（江苏省竞赛试题）

11．已知△OAB，△OCD都是等腰直角三角形，∠AOB＝∠COD＝90°

．

（1）如图1，点C在OA边上，点D在OB边上，连接AD，BC，M为线段AD的中点，求证：

OM⊥BC．

（2）如图2，在图1的基础上，将△OCD绕点O逆时针旋转α（α为锐角），M为线段AD的中点．

①求证：

OM＝

BC；

②OM⊥BC是否还成立?

若成立，请证明；

若不成立，请说明理由．

12．如图1，在△ABC中，点P为BC边的中点，直线a绕顶点A旋转，若点B，P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM，PN．

（1）延长MP交CN于点E（如图2）．

△BPM≌△CPE；

②求证：

PM＝PN．

（2）若直线a绕点A旋转到如图3的位置时，点B，P在直线a的同侧，其他条件不变，此时PM＝PN还成立吗？

（3））若直线a绕点A旋转到与BC边平行的位置时，其他条件不变．请直接判断四边形MBCN的形状及此时PM＝PN是否成立．不必说明理由．（沈阳市中考试题）