七年级下册复习Word文件下载.docx

七年级下册复习Word文件下载.docx

《七年级下册复习Word文件下载.docx》由会员分享，可在线阅读，更多相关《七年级下册复习Word文件下载.docx（15页珍藏版）》请在冰豆网上搜索。

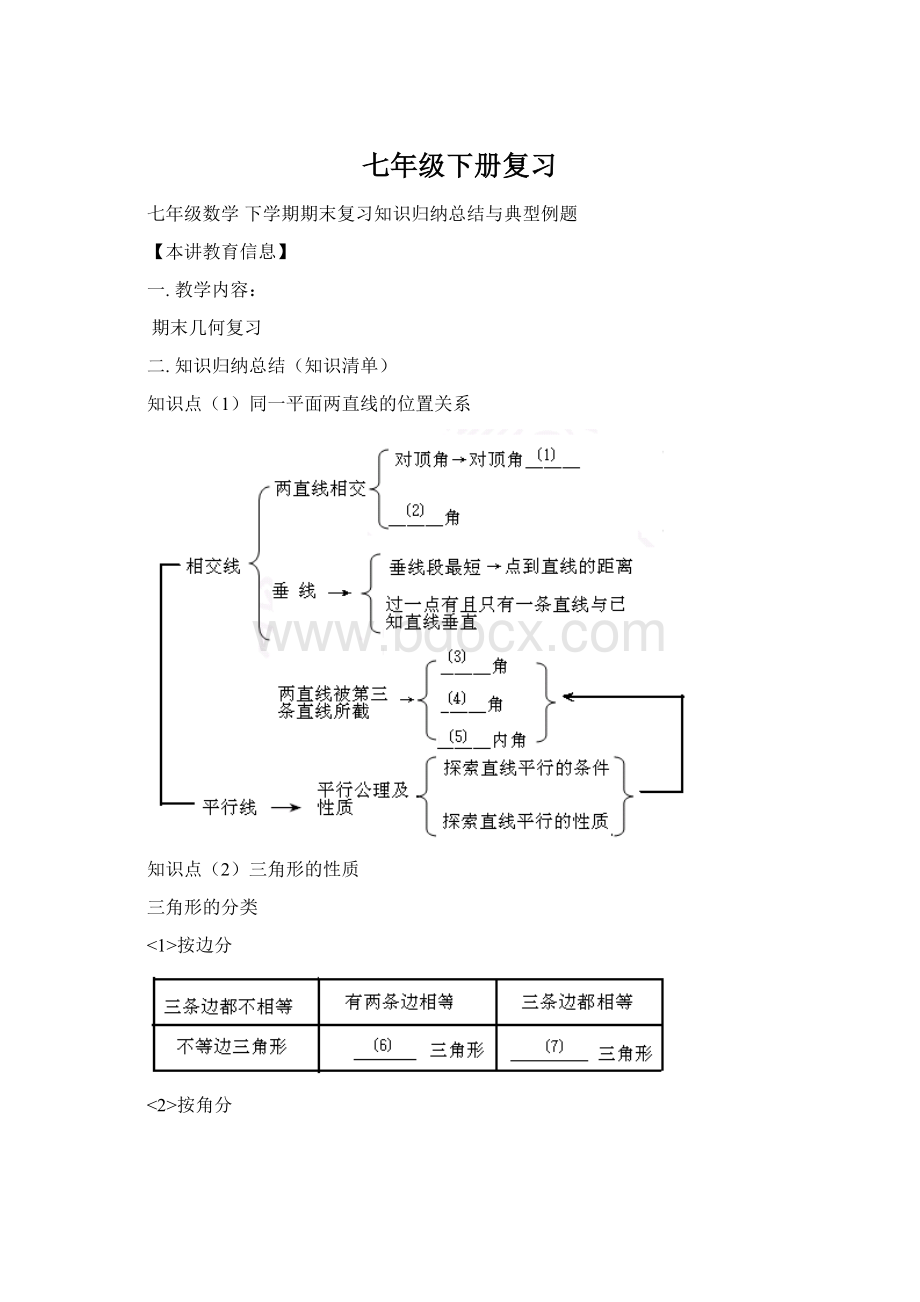
则∠3＝＿＿＿

解析：

∵a∥b（已知）

∴∠2＝∠DBC＝65°

（两直线平行，内错角相等）

∵∠DBC＝∠1＋∠3（三角形的一个外角等于与它不相邻的两个内角之和）

∴∠3＝∠DBC－∠1

＝65°

－20°

＝45°

本题考查平行线性质和三角形的外角性质的应用

例二．将一副三角板如图放置，已知AE∥BC，则∠AFD的度数是【】

A．45°

B．50°

C．60°

D．75°

∵AE∥BC（已知）

∴∠C＝∠CAE＝30°

∵∠AFD＝∠E＋∠CAE（三角形的一个外角等于与它不相邻的两个内角之和）

＋30°

=75°

故选D

本题解答时应抓住一副三角板各个角的度数

例三．如图，∠1＋∠3＝180°

，CD⊥AD，CM平分∠DCE，求∠4的度数

∵∠3＝∠5（对顶角相等）∠1＋∠3＝180°

（已知）

∴∠1＋∠5＝180°

（等量代换）

∴AD∥BE（同旁内角互补，两直线平行）

∵CD⊥AD（已知）

∴∠6＝90°

（垂直定义）

又∵AD∥BE（已证）

∴∠6＋∠DCE＝180°

（两直线平行，同旁内角互补）

∴∠DCE＝90°

又∵CM平分∠DCE（已知）

∴∠4＝∠MCE＝45°

（角平分线定义）

例四．如图，已知AB∥CD，∠1＝110°

，∠2＝125°

，求∠x的大小

【分析】因为∠x＋∠AEC＝180°

，要求∠x，需求∠AEC．观察图形，∠1、∠2、∠AEC没有直接联系，由已知AB∥CD，可以联想到平行线的性质，所以添加EF∥AB，则∠1、∠2、∠3、∠4、∠x之间的关于就比较明显了

解：

过E点作EF∥AB

∴∠1＋∠3＝180°

∴∠3＝180°

－∠1

＝180°

－110°

＝70°

∵AB∥CD（已知），AB∥EF（作图）

∴CD∥EF（两直线都平行于第三条直线，那么这两条直线也平行）

∴∠4＋∠2＝180°

∴∠4＝180°

－∠2

－125°

＝55°

∴∠x＝180－∠3－∠4

－70°

－55°

例五、在平面直角坐标系中，到x轴的距离等于2，到y轴的距离等于3的点的坐标是__________。

到x轴的距离等于2的点的纵坐标有－2、＋2；

到y轴的距离等于3的点的横坐标有＋3、－3，因此，满足条件的点的坐标有（3，2）、（3，－2）、（－3，2）、（－3，－2）

例六、如图所示，在平面直角坐标系中，平行四边形ABCD的顶点A、B、D的坐标分别是（1，1）、（3，3）、（－4，1），则顶点C的坐标是＿＿＿

∵A点纵坐标和D点的纵坐标相等

∴AD∥x轴

又∵AD∥BC

∴BC∥x轴

∴B点和C点的纵坐标相等

∴C点纵坐标是3

又∵A点与D点的距离为5〖｜1－（－4）｜横坐标差的绝对值〗

∴B、C两点距离也为5（AD＝BC）

∴C点的横坐标是－2

∴C点的坐标是（－2，3）

例七、在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A′的坐标是（－2，2），现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点

（1）请画出平移后的图像△A′B′C′（不写画法），并直接写出点B′、C′的坐标：

B′（＿＿＿＿＿）、C′（＿＿＿＿＿＿）

（2）若△ABC内部一点P的坐标是（a，b），则点P的对应点P′的坐标是（＿＿＿＿＿）

（1）图略由A和A′的坐标可知：

A点向左平移5个单位，再向下平移2个单位得到

A′，所以B′坐标是（－4，1）；

C′坐标是（－1，－1）

（2）．P′坐标是（a－5，b－2）

例八、若点（9－a，a－3），在一、三象限角平分线上，求a的值

因为点（9－a，a－3）在一、三象限角平分线上，所以9－a＝a－3，解得a＝6

【点评】抓住一、三象限角平分线上的点的坐标特征：

横、纵坐标相等，可将问题转化为a的一元一次方程

三角形

例九、如图，在△ABC中，∠A：

∠B：

∠C＝3：

4：

5，BD、CE分别是边AC、AB上的高，BD、CE相交于H，求∠BHC的度数

设∠A＝3x°

，则∠B＝4x°

，∠C＝5x°

∵∠A＋∠ABC＋∠ACB＝180°

（三角形三内角和为180°

）

∴3x°

＋4x°

＋5x°

＝180°

即12x°

∴x°

＝15°

∴∠A＝45°

∴∠ABD＝90°

－45°

＝45°

又∵∠BHC＝∠BEC＋∠ABD（三角形的一个外角等于与它不相邻的两个内角之和）

＋90°

＝135°

【点评】数学计算中经常涉及比的问题，用设比例系数的方法来解决，如本题中的比例系数为x

例十、下列各组中的数分别表示三条线段的长度，试判断以这些线段为边能否组成三角形

①3、5、2；

②a、b、a＋b（a＞0，b＞0）；

③3、4、5；

④m＋1、2m、m＋1（m＞0）；

⑤a＋1、2、a＋5（a＞0）

①∵3＋2＝5，∴以这三条线段为边不能组成三角形

②∵a＋b＝a＋b∴以a、b、a＋b为边的三条线段不能组成三角形

③∵3＋4＞5∴以3、4、5为边的三条线段能组成三角形

④∵（m＋1）＋（m＋1）＝2m＋2＞2m，

且（m＋1）＋2m＝3m＋1＞m＋1

∴以m＋1、2m、m＋1为边的三条线段能组成三角形

⑤∵（a＋1）＋2＝a＋3＜a＋5∴以a＋1、2、a＋5为边的三条线段不能组成三角形

【点评】三角形三边关系可以用来判定已知三条线段的长，它们是否可以组成三角形，若能判断出最长的一条时，就只要将较小两边的和与最长的这一边比较；

若不能判断哪一条最长，必须任意两边之和都大于第三边才可以

例十一、多边形的一个外角与其内角和的度数总和为600°

，求此多边形的边数。

设多边形的边数为n，一个外角为x°

依题意得（n－2）180°

＋x°

＝600°

即（n－2）180°

－x°

∵（n－2）180°

是180°

的倍数

∴600°

－x也是180°

∴x°

＝60°

，n＝5

∴此多边形的边数为5

例十二、如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G的度数

【观察图形可知，此图形是由一个△ACE和一个四边形BDFG构成】

∵∠A＋∠C＋∠E＝180°

又∵∠B＋∠D＋∠F＋∠G＝360°

（四边形内角和为360°

∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝180°

＋360°

＝540°

【点评】若直接求出每一个角的度数再求其和显然是做不到的，因此，设法整体求值是解题的关键

【模拟试题】

（答题时间：

60分钟）

一、选择题

1．给出下列说法：

①两条直线被第三条直线所截，同位角相等

②平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交

③相等的两个角是对顶角

④从直线外一点到这条直线的垂线段，叫做这点到直线的距离

其中正确的有【】

A．0个B．1个C．2个D．3个

2．如图，AB⊥BC，BD⊥AC，能表示点到直线（或线段）的距离的线段有【】

A．1条B．2条C．4条D．5条

3．过A（4，－2）和B（－2，－2）两点的直线一定【】

A．垂直于x轴B．与y轴相交但不平行于x轴

C．平行于x轴D．与x轴、y轴都平行

4．已知三角形的三个顶点坐标分别是（－1，4），（1，1），（－4，－1），现将这三个点先向右平移2个单位长度，再向上平移3个单位长度，则平移后这三个顶点的坐标是【】

A．（－2，2），（3，4），（1，7）B．（－2，2），（4，3），（1，7）

C．（2，2），（3，4），（1，7）D．（2，－2），（3，3），（1，7）

5．以7和3为两边的长，另一边长为整数的三角形一共有【】

A．3个B．4个C．5个D．6个

6．三角形一个外角小于与它相邻的内角，这个三角形是【】

A．直角三角形B．锐角三角形C．钝角三角形D．不能确定

7．4根火柴棒形成如图所示的“口”字，平移火柴棒后，原图形能变成的象形汉字是【】

8．点P（x＋1，x－1）一定不在【】

A．第一象限B．第二象限C．第三象限D．第四象限

9．如果一个多边形除了一个内角外，其余各角的和为2030°

，则这个多边形的边数是【】

A．12条B．13条C．14条D．15条

10．如果∠A和∠B的两边分别平行，那么∠A和∠B的关系【】

A．相等B．互余或互补C．互补D．相等或互补

二、填空题

1．如图所示，由点A测得点B的方向为＿＿＿＿＿＿＿

2．如图所示，BE是AB的延长线，量得∠CBE＝∠A＝∠C

（1）．由∠CBE＝∠A可以判断＿＿＿＿＿∥＿＿＿＿＿＿，根据是＿＿＿＿＿＿＿＿，

（2）．由∠CBE＝∠C可以判断＿＿＿＿＿∥＿＿＿＿＿＿，根据是＿＿＿＿＿＿＿＿，

3．如图所示，直线L1∥L2，AB⊥L1，垂足为点O，BC与L2相交于点E，若∠1＝43°

，则∠2＝＿＿＿＿

4．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝55°

，则∠2＝＿＿＿＿＿

5．把一副三角板按如图所示的方式摆放，则两条斜边所成的钝角x为＿＿＿＿＿＿＿

6．在多边形的内角中，锐角的个数不能多于＿＿＿＿＿

7．若一个正多边形的每一个外角都是30°

，则这个正多边形的内角和等于＿＿＿＿＿

8．已知点A（a，0）和点B（0，5）两点，且直线AB与坐标轴围成的三角形的面积等于10，则a的值是＿＿＿＿＿

9．等腰三角形ABC的边长分别为4cm，3cm，则其周长为＿＿＿＿＿

10．如图，AB＝A1B，A1C＝A1A2，A2D＝A2A3，A3E＝A3A4，∠B＝20°

，则∠EA3A4的度数是＿＿＿＿

三、解答题

1．如图，当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，在图中，∠1＝43°

，∠2＝27°

，试问光的传播方向改变了多少度？

2．如图，已知∠1＋∠2＝180°

，∠3＝∠B，试判断∠AED与∠C的关系

3．解答下列各题

（1）．已知点P（a－1，3a＋6）在y轴上，求点P的坐标

（2）．已知两点A（－3，m），B（n，4），若AB∥x轴，求m的值，并确定n的范围

4．在如图所示的直角坐标系中，三角形ABC的顶点坐标分别是A（0，0）、B（6，0）、C（5，5）

（1）．求三角形ABC的面积

（2）．如果将△ABC向上平移3个单位长度，得到△A1B1C1，再向右平移2个单位长度，得到△A2B2C2，分别画出△A1B1C1和△A2B2C2，并求出A2、B2、C2的坐标

5．一个多边形的内角和是它的外角和的4倍，求

（1）．这个多边形是几边形

（2）．这个多边形共有多少条对角线

6．在△ABC中，∠A：

5，BD、CE分别是AC、AB边上的高，BD、CE相交于点H，求∠BHC的度数

【试题答案】

一．选择题

1．B2．D3．C4．A5．C6．C7．B8．B

9．C10．D

二．填空题

1．南偏东60°

2．

（1）．AD∥BC同位角相等，两直线平行

（2）．CD∥AE内错角相等，两直线平行3．133°

4．35°

5．165°

6．3个7．1800°

8．4或－49．10cm或11cm10．160°

三．解答题

1．解析：

若光路不发生改变，则∠BFD＝∠1＝43°

，光路改变后，∠2＝27°

则∠DFE＝∠BFD－∠2＝43°

－27°

＝16°

，所以光的传播方向改变了16°

2．解析：

∵∠2＋∠ADF＝180°

（邻补角）

又∵∠1＋∠2＝180°

∴∠1＝∠ADF（同角的补角相等）

∴AB∥EG（同位角相等，两直线平行）

∴∠3＝∠ADE（两直线平行，内错角相等）

又∵∠3＝∠B（已知）

∴∠B＝∠ADE（等量代换）

∴BC∥DE（同位角相等，两直线平行）

∴∠AED＝∠C（两直线平行，同位角相等）

3．解析：

（1）．∵点P在y轴上，∴a－1＝0，∴a＝1，∴点P坐标为（0，9）

（2）．∵AB∥x轴∴m＝4，n≠3

4．解析：

（1）．由图可知△ABC的底AB为6，高为C点的纵坐标等于5，

所以△ABC的面积＝0．5×

6×

5＝15

（2）△A1B1C1与△A2B2C2如下图所示，A2（2，3）、B2（8，3）、C2（7，8）

5．解析：

（1）．设这个多边形是n边形，则（n－2）

180°

＝4×

360°

，

∴n＝10

（2）．10

（10－3）÷

2＝35（条）

6．解析：

设∠A＝3x，∠B＝4x，∠C＝5x

∵∠A＋∠B＋∠C＝180°

（三角形三内角和等于180°

∴3x＋4x＋5x＝180°

∴x＝15°

，∠B＝60°

，∠C＝75°

∵四边形AEHD内角和等于360°

∴∠A＋∠AEH＋∠ADH＋∠EHD＝360°

∵CE⊥AB；

BD⊥AC

∴∠AEH＝90°

，∠ADH＝90°

∴45°

＋∠EHD＝360°

∴∠EHD＝135°

∵∠BHC＝∠EHD＝135°

（对顶角相等）