数模校赛送货线路设计问题原创Word文件下载.docx
《数模校赛送货线路设计问题原创Word文件下载.docx》由会员分享,可在线阅读,更多相关《数模校赛送货线路设计问题原创Word文件下载.docx(21页珍藏版)》请在冰豆网上搜索。
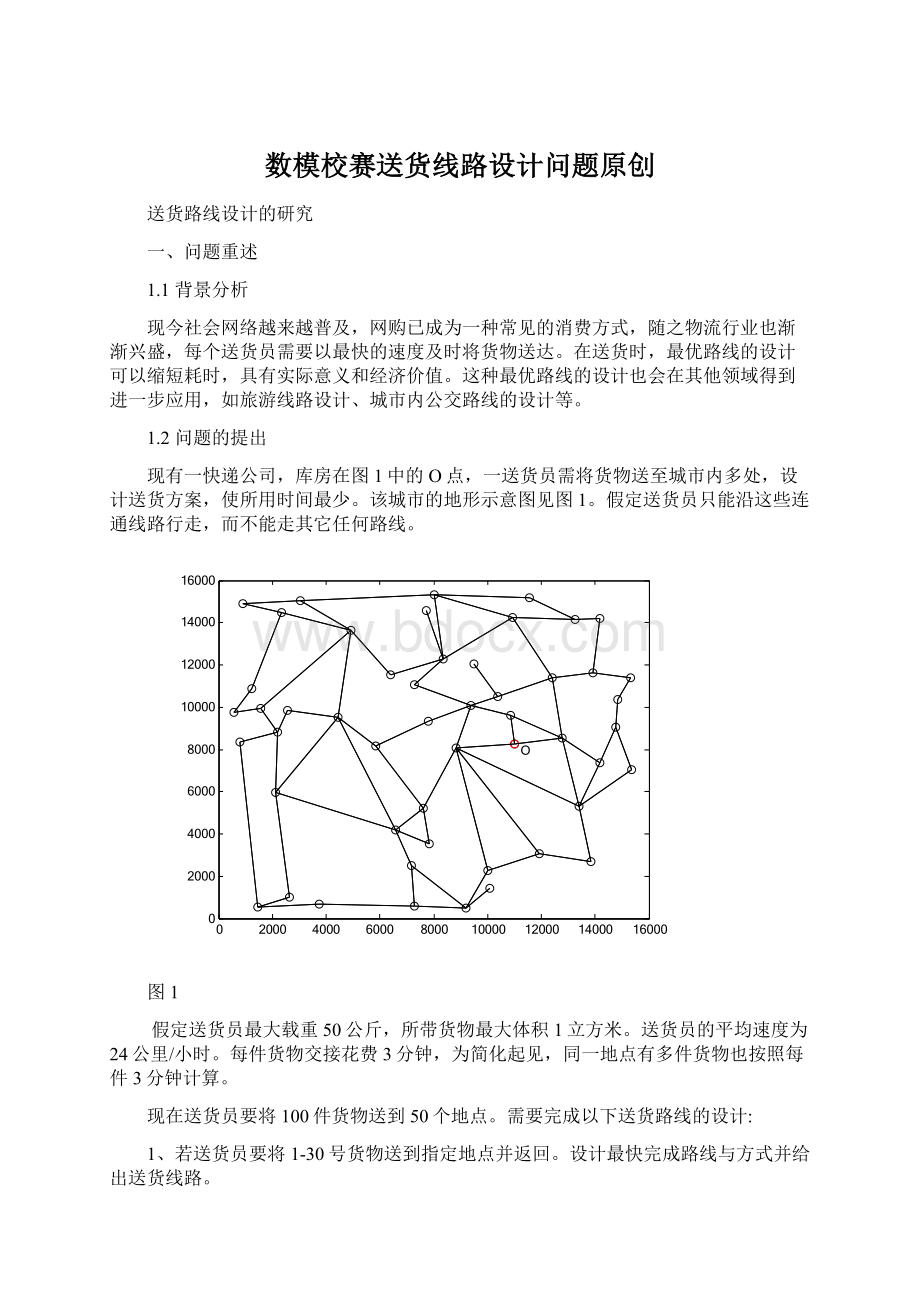
,
为节点个数,这样将导致随着
的增大,复杂度成指数形式增长,当
时该方法几乎不可能实现,目前已经证明TSP问题是NP-难的。
目前的解法主要有遗传算法、最小生成树、模拟退火、蚁群法、局部搜索、神经网络等。
3.2算法一的建立
我们采用近似算法——二边逐次修正法来求该问题的近似最优解。
并由矩阵翻转法(见附录2)实现。
任意给定一个图G,求最优H圈的具体算法如下:
(1)由
构造出完备图
(2)用随机排列生成
的若干个H圈,例如200个;
(3)在所得到的每个H圈中,用二边逐次修正法进行优化,得到近似最佳H圈;
(4)在得到的所有H圈中找出权最小的一个,此即要找的最佳近似H圈。
3.3问题一
首先,由初始数据构造初始带权图D(其邻接矩阵D(51,51)见附录1)。
用floyd算法(见附录3)求出51个顶点的完备图Y(其邻接矩阵Y(51,51)见附录1)及其路由矩阵R。
(为了方便,我们设O为51号点)
前30号货物要送到21个送货点并返回,由于前30号货物总重、总体积分别为48、0.88,故只需一次就可以送完。
故问题转化为求解由O点出发,经过21个送货点仅一次并回到O点的最佳H圈。
基于这种想法,通过遍历完备图Y的邻接矩阵得到O点及21个送货点生成的连通子图A(其邻接矩阵A(22,22),见附录1)。
通过算法一可以求出最优的H圈,由于设定不同的初始H圈得到的最优H圈不同,我们用200个随机产生的初始H圈分别求解,在所得的200组解中选择总路程最小的一组,结果为:
O-18-13-24-31-27-39-34-40-45-42-49-43-36-38
-32-23-16-14-17-21-26-O(矩阵翻转法的具体求解过程见附录1)
总路程为:
54708(m).
最后,我们通过完备图Y的路由矩阵R,求出每两个送货点间经过的不必停留的点,得到最佳送货路线:
O-18-13-19-24-31-27-39-27-31-34-40-45-42-49
-42-43-38-36-38-35-32-23-16-14-17-21-26-O
(其中加删除线的点包括不必送货的点及已经经过一次的点。
)
在城市地形图上标记出最佳送货路线,见图2。
图2
3.4问题二
第二问是一个有约束条件的最优H圈问题,在第一问的基础加入了时间的限制。
同样由于货物总重量、体积均未超过上限,因此只运送一次即可。
我们采用两种方法来求解第二问。
方法一:
先不考虑时间限制,用第一问的方法,给定200个初始H圈,分别求出对应的最优H圈。
然后从所有的200个最优H圈中选择总距离最小的若干种最佳路线,再挑选出其中满足限制条件且总距离最小的一种路线。
求解过程可列表表示如下:
最优路线一
初始H圈
O,16,18,27,39,21,42,34,23,24,38,13,31,26,17,45,49,43,14,40,32,36,O
最优路线
O,18,13,24,27,39,36,21,17,14,16,23,32,38,43,49,42,45,40,34,31,26,O
最短路程
54994
送货到各点耗时(h)
0,0.05,0.29,0.41,0.55,0.72,0.85,0.99,1.15,1.29,1.39,1.55,1.70,1.79,1.92,2.15,2.34,2.46,2.60,2.73,3.02,3.20,3.34
表1
最优路线二
O,24,34,14,27,13,26,16,38,39,45,21,31,43,17,32,23,40,49,42,36,18,O
0,18,13,24,31,27,39,34,40,45,42,49,43,38,36,32,23,16,14,17,21,26,O
54708
0,0.09,0.27,0.56,0.68,0.78,0.90,1.17,1.28,1.47,1.61,1.74,1.92,2.08,2.19,2.41,2.51,2.65,2.81,2.95,3.08,3.22,3.33
表2
最优路线三
O,13,40,14,39,42,43,24,27,34,49,26,31,21,17,16,18,36,23,32,45,38,O
O,26,21,17,14,16,23,32,38,43,49,42,45,40,34,31,36,39,27,24,13,18,O
56041
0,0.05,0.19,0.32,0.46,0.62,0.76,0.86,1.02,1.18,1.35,1.48,1.63,1.81,1.93,2.08,2.26,2.48,2.60,2.77,3.06,3.24,3.39
表3
最优路线四
O,32,40,39,45,27,34,38,21,43,17,26,24,49,31,16,23,18,14,42,13,36,O
O,13,18,31,24,27,39,34,40,45,49,42,43,36,38,32,23,16,14,17,21,26,O
55991
0,0.22,0.40,0.53,0.66,0.83,0.95,1.22,1.33,1.52,1.75,1.88,1.97,2.19,2.31,2.46,2.57,2.70,2.86,3.00,3.13,3.27,3.38
表4
比较可知:
最优路线二的总路程最短,且完全符合时间的要求。
即最佳路线(同第一问的最佳路线)为:
0-18-13-24-31-27-39-34-40-45-42-49-43-38-36
-32-23-16-14-17-21-26-O。
送完所有货物的时间为11:
16。
在城市地形图上标记出最佳送货路线,见图3。
图3
方法二:
由于各送货点的时间限制只有9:
00,9:
30,10:
15,12:
00四种,我们可以把21个送货点按时限顺序分成四组。
先送第一组(时限为9:
00),再送第二组,以此类推。
我们可以通过求解最优H圈的方法求出运送每一批货物选择的最佳路线。
我们只需要判断每组的最后一个运送点是否满足时间限制即可。
具体方法如下:
(1)送货员先通过第一组送货点,用O点和18,13,24(时限为9:
00)共四个点生成连通子图。
利用二边逐次修正TSP算法求出最佳H圈,去掉最后一条边,得到最佳路径及送完第一组送货点的时间。
设该路径的最后一个点为V。
(2)以V为起点通过第二组送货点,用V点和31,34,40,45共五个点生成连通子图。
利用二边逐次修正TSP算法求出最佳H圈,去掉最后一条边,得到最佳路径送完第二组送货点的时间。
(3)重复上述的步骤,得到送第三组、第四组货物的最佳路径。
批次
截止时间
最佳货物运送路线
该批运送完的时间
第一批
9:
00
O-18-13-24
8:
36
第二批
30
31-34-40-45
11
第三批
10:
15
42-49-43-38
48
第四批
12:
36-27-39-26-21-17-14-16-23-32
11:
13
表5
在城市地形图上标记出最佳送货路线,见图4。
图4
比较方法一和方法二所得的最优解:
方法一送完所有货物的时间为11:
16,送完货物回到O点的时间为11:
20;
方法二送完所有货物的时间为11:
13,送完货物回到O点的时间为11:
29。
可见两种运送路线各有优劣:
如果要求完成送货最快,可选用方法二所得最优路线;
如果要求完成送货并回到O点所用时间最少,可选用方法二所得最优路线。
3.5问题三
由于100件货物的总重量为148,总体积为2.8,送货员须至少往返3次才能将货物送完。
因此可以考虑将1-50号送货点分为三组,每次运送其中的一组。
分组应满足以下原则:
(1)每组送货点应当尽量接近,实现尽可能少的重复路径。
(2)要保证送到每一组的货物总重量、总体积均满足限制条件。
将顶点分组后,将原问题转化为三个独立的有限制的TSP组合优化问题。
首先我们进行初步分组:
从O点出发到其他点,要使总路程最小应尽量走O点到该点的最短路,故用用Dijkstra算法(见附录二)求出O点到其余顶点的最短路,并构成一棵一O为根的最小生成树。
(尽管我们已经用floyd算法求出了各点间的最短距离,但Dijkstra算法产生的路由矩阵更便于我们画出最小生成树。
得到的最小生成树如图5:
图5
将50个点按所在干枝分为三组,记为
、
,如图所示。
分别计算各干枝上的点的要送货物的重量和体积:
①
②
③
总质量
61.97
57.63
28.4
总体积
1.0988
1.0868
0.6144
表6
我们可以看出对于重量的限制较为严格,对于体积的限制相对宽松。
因此根据重量的限制进行进一步调整,调整的规则是:
(1)在
中各选出一个点,使这三个点中两两之间的最短路长度是这样的所有的三点组中最大的,作为各组的基点。
通俗地说,就是找到图中“分的最开”的三个点作为基点。
(2)选出
三组中重量最大和最小的点。
(3)在上述重量最大的组中找到与重量最小的组的基点最近的点,并把它转移到现在重量最小的组,构成一个新的分组。
重新求三组的总重量。
(4)重复上述步骤
(2)和步骤(3),直到三组的重量均符合要求(小于50)。
如果此时体积也符合要求,则得到最佳的分组方式。
具体求解过程见表7:
调整次数
调整前三组送货点的送货总重量
调整前三组送货点的送货总体积
要调整的点
调整方法
1
1.098
0.614
1.086
20
①→②
2
59.75
30.62
1.017
0.695
22
3
59.36
31.01
19
4
54.37
0.966
0.747
9
③→②
5
38.14
55.49
0.755
1.078
14
6
41.52
52.11
0.814
1.019
29
7
53.03
42.86
0.929
0.852
8
52.97
42.92
0.888
0.892
25
48.48
47.41
0.877
0.903
45
③→①
10
53.52
47.07
1.016
0.880
26
①→③
49.13
51.46
0.954
0.942
49
12
51.49
49.1
1.025
0.871
28
49.77
0.967
0.961
停止调整
表7
在求得的最小生成树上标记出分组情况,见图6。
图6
(图中“o”表示分到
组的点,“x”表示分到
组的点,“*”表示分到
组的点。
然后,将O点分别归入三个分组中,求出每个分组的点构造的三个连通子图,用算法一求出每次运送的最佳路线,结果见表8:
次别
总路程
第一次
O-27-39-45-49-50-44-48-46-33-41-37-47-40-34-31-24-O
59520
第二次
O-14-9-10-7-1-6-8-3-4-2-5-15-20-22-28-30-29-25-19-12-11-13-18-O
61960
第三次
O-26-36-38-43-42-35-32-23-16-17-21-O
28237
表8
在图上标出三条最优路线,见图7
图7
三次送货总路程为:
149717(m),由此求出运送完所有货物的时间为:
16:
44。
四、模型的评价与推广
4.1、模型的评价
1、目前已经证明TSP问题是NP-难的,不存在多项式的精确算法,而TSP近似算法包括构造性算法和改进型算法。
构造性算法是按一定规则一次性的构造出一个解,而改进型算法则是逐步迭代改进解。
本文利用的是改进型算法-二边逐次修正法来近似得到TSP问题的最优解。
该算法算法都有成熟的理论基础,又有相应的软件支持,可信度高。
2、二边逐次修正法传统的实现过程比较麻烦,而且当顶点数较多的时候,甚至没办法求解。
本文算法一用矩阵翻转方法来实现二边逐次修正法过程,编程容易,程序简洁、独立,计算速度非常快,而且适用顶点数目较多的情况。
3、在利用算法一进行计算时,随机生成大量初始H圈,能够以极高的概率找到最优解。
4、第二问中我们采用两种方法分别得到两组最优路线,比对其进行了比较。
5、第三问中利用最小生成树对50个点分组,然后进一步调整,调整的原则明确,人为干预性较小。
6、图形图像结合,输出结果更加直观。
模型求解时,采用分析-假设-建模-编程-验证的步骤,整个过程科学严谨,结果详细明确。
4.2模型的推广
该送货线路问题的模型具有广泛的适用性,由对该问题的理解将其进行推广到信件邮递、公交线路设计以及仓库选址等领域,
五、参考文献
[1]赵静等,数学建模与数学实验,北京:
高等教育出版社,2006
[2]武波,离散数学,陕西:
西安电子科技大学出版社,2007
[3]杨秀文等,利用矩阵翻转法求最佳H圈,后勤工程学院学报,VoL.24No.1Jan.2008
六、附录
6.1附录一
初始带权图D的邻接矩阵D(51,51):
(只摘录前8行8列)
Inf
1916.3
1294.3
1968.2
2863.8
2292.6
1252.9
3536.4
1958.1
表9
51个顶点的完备图Y的邻接矩阵Y(51,51):
7745.3
5452.7
8998.3
5829.1
9039.6
9713.6
7787.1
7082
3210.6
3884.5
3545.6
6747
7420.9
5494.5
10293
10967
9040.1
3262.6
4158.1
4832
表10
由O点及21个送货点生成的连通子图A的邻接矩阵A(22,22):
3996.8
1796.9
11722
5395.4
5776.8
4677.1
5093.7
4796.5
9248.8
7576.9
1779.9
2203.9
8093.3
9925.1
3598.4
6576.4
2880.2
3296.7
9343.1
11029
7044.9
13222
9356.9
5373
3970.2
3983.8
9873.2
6176.9
表11
6.2附录二
6.2.1矩阵翻转法的引入
首先以一个六顶点的图为例(见图8),用二边逐次修正法在完备加权图中寻求最佳哈密尔顿圈。
如选取初始圈
其总权为237。
由于
(见图9),所以去掉边
,添加边
,得到较优的H圈为:
,其总权为210,如图10。
图8完备图图9对初始圈改进图10较优H圈
可用“矩阵翻转”来实现上述过程:
将完备加权图8用距离矩阵表示,使所选的初始圈为矩阵的主对角线的上方元素对应的顶点:
对角线上方元素对应的顶点就组成初始圈的路线:
,其经过的权为237.如果所选初始H圈不是
,可通过交换距离矩阵A的行和列,使矩阵的主对角线的上方元素对应的顶点为所选的初始H圈。
为了能看到翻转效果和更直观确定优化后H圈所走的路线,在第一行和最后一行给距离矩阵加上了一个点的排列顺序的框,与此同时为了使矩阵仍然保持为方阵,在第一列和最后一列加上2个0列(或者在距离矩阵第一行、列和最后一行、列同时加上一个点的排列顺序的框):
矩阵变化后,相应的顶点顺序也在变化,但对角线上方元素仍组成H圈的路线。
。
在A中,存在A(2,5)+A(3,6)<
A(2,3)+A(5,6),所以把矩阵A第3至5列翻转、第3至5行也翻转,得到:
除边框元素外,对角线上方元素或矩阵的第一行点序列组成新的H圈为
总权为210,是较优H圈。
依据上面的分析,用矩阵翻转在完备加权图中寻求最佳日圈的整个实现过程如下:
(1)一个完备加权图中,任取初始H圈,按其点顺序可组成一个距
离矩阵A
(2)给A在第一行和最后一行加一个点的排列顺序框,同时在第一列和最后一列加上2个0列。
(3)在加点序框的距离矩阵A中,对所有的i,j,2<
i+1<
j<
n-2,当A(i,j)+A(i+1,j+1)<
A(i,i+1)+A(j,j+1)成立时,把第i+1至j列翻转过来,第i+1至j行也翻转,形成新的距离矩阵.
(4)对A重复执行步骤3,直到条件不满足为止,最后得到的C即为近似最佳H圈。
Matlab源程序如下:
function[e,s]=h(E)%E为按照初始H圈点的顺序组成的含点序边框的距离矩阵.e为最优H圈对应的矩阵,s为最小路程
n=size(E);
fori=2:
n-2
forj=i+1:
n-2;
ifE(i,j)+E(i+1,j+1)<
E(i,i+1)+E(j,j+1)
a=horzcat(E(:
1:
i),E(:
j:
-1:
i+1),E(:
j+1:
n));
%翻转e中的第i+1至j列
b=vertcat(a(1:
i,:
),a(j:
i+1,:
),a(j+1:
n,:
));
%翻转a中的第i+1至j行
E=b;
end
end
s=0;
s=s+E(i,i+1);