高考数学大一轮复习第十二章概率随机变量及其分布124离散型随机变量及其分布列教师用书理新人教Word文档格式.docx
《高考数学大一轮复习第十二章概率随机变量及其分布124离散型随机变量及其分布列教师用书理新人教Word文档格式.docx》由会员分享,可在线阅读,更多相关《高考数学大一轮复习第十二章概率随机变量及其分布124离散型随机变量及其分布列教师用书理新人教Word文档格式.docx(15页珍藏版)》请在冰豆网上搜索。
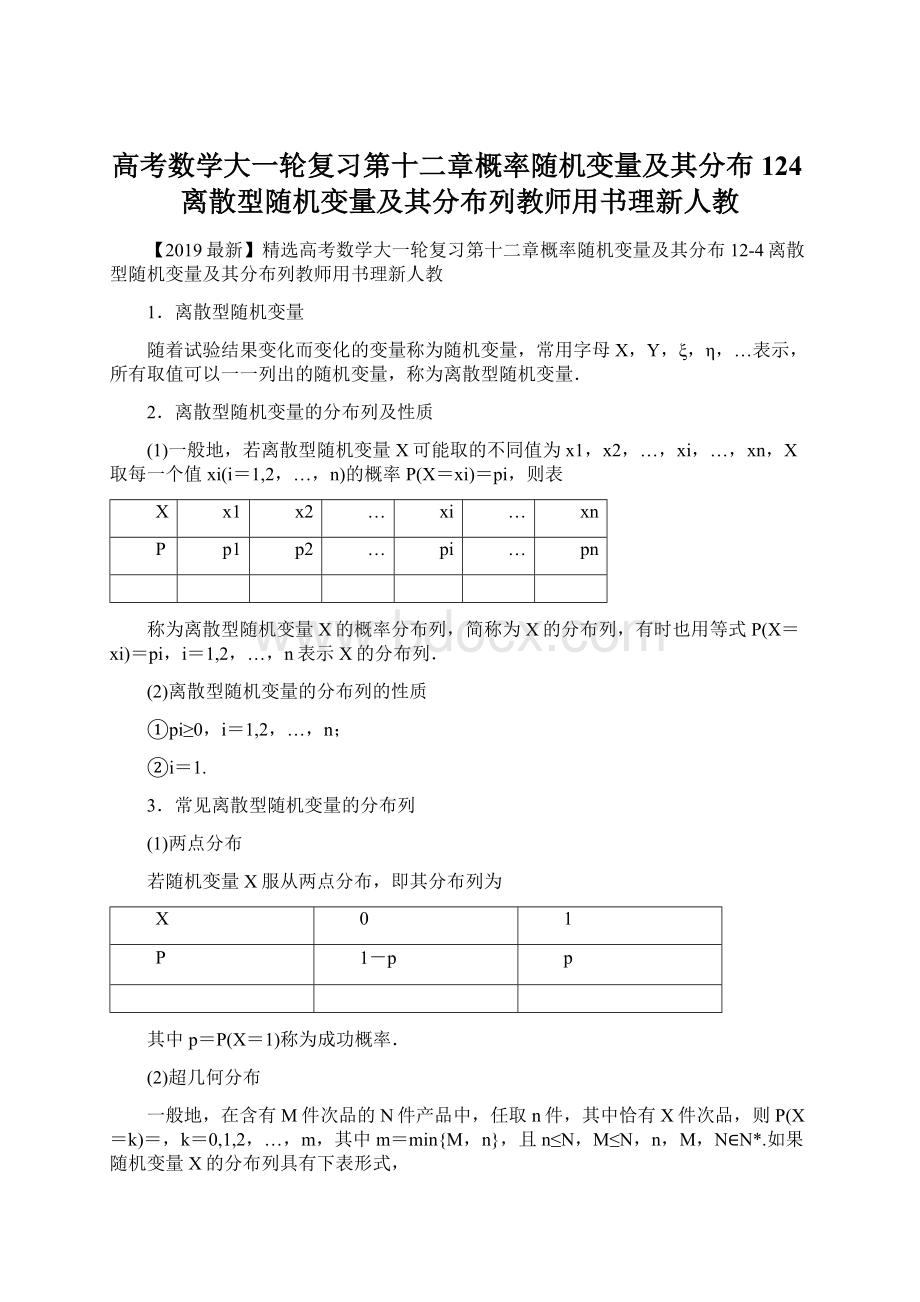
(2)离散型随机变量的分布列描述了由这个随机变量所刻画的随机现象.( √ )
(3)某人射击时命中的概率为0.5,此人射击三次命中的次数X服从两点分布.( ×
)
(4)从4名男演员和3名女演员中选出4名演员,其中女演员的人数X服从超几何分布.( √ )
(5)离散型随机变量的分布列中,随机变量取各个值的概率之和可以小于1.( ×
(6)离散型随机变量的各个可能值表示的事件是彼此互斥的.( √ )
1.(教材改编)抛掷甲、乙两颗骰子,所得点数之和为X,那么X=4表示的事件是( )
A.一颗是3点,一颗是1点
B.两颗都是2点
C.甲是3点,乙是1点或甲是1点,乙是3点或两颗都是2点
D.以上答案都不对
答案 C
解析 根据抛掷两颗骰子的试验结果可知,C正确.
2.设某项试验的成功率是失败率的2倍,用随机变量X去描述1次试验的成功次数,则P(X=0)等于( )
A.0B.C.D.
解析 设X的分布列为
2p
即“X=0”表示试验失败,“X=1”表示试验成功,由p+2p=1,得p=,故选C.
3.从标有1~10的10支竹签中任取2支,设所得2支竹签上的数字之和为X,那么随机变量X可能取得的值有( )
A.17个B.18个C.19个D.20个
答案 A
解析 X可能取得的值有3,4,5,…,19,共17个.
4.从装有3个红球、2个白球的袋中随机取出2个球,设其中有X个红球,则随机变量X的分布列为
2
答案 0.1 0.6 0.3
解析 ∵X的所有可能取值为0,1,2,
∴P(X=0)==0.1,
P(X=1)===0.6,P(X=2)==0.3.
∴X的分布列为
0.1
0.6
0.3
5.(教材改编)一盒中有12个乒乓球,其中9个新的、3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,则P(X=4)的值为______.
答案
解析 由题意知取出的3个球必为2个旧球、1个新球,
故P(X=4)==.
题型一 离散型随机变量的分布列的性质
例1
(1)设X是一个离散型随机变量,其分布列为
-1
2-3q
q2
则q等于( )
A.1B.±
C.-D.+
解析 ∵+2-3q+q2=1,∴q2-3q+=0,解得q=±
.又由题意知0<
q2<
,∴q=-.
(2)设离散型随机变量X的分布列为
3
4
0.2
求2X+1的分布列.
解 由分布列的性质知
0.2+0.1+0.1+0.3+m=1,得m=0.3.
首先列表为
2X+1
5
7
9
从而2X+1的分布列为
引申探究
1.在本例
(2)的条件下,求随机变量η=|X-1|的分布列.
解 由
(2)知m=0.3,列表
|X-1|
∴P(η=1)=P(X=0)+P(X=2)=0.2+0.1=0.3,
P(η=0)=P(X=1)=0.1,P(η=2)=P(X=3)=0.3,
P(η=3)=P(X=4)=0.3.
故η=|X-1|的分布列为
η
2.若本例
(2)中条件不变,求随机变量η=X2的分布列.
解 依题意知η的值为0,1,4,9,16.
P(η=0)=P(X2=0)=P(X=0)=0.2,
P(η=1)=P(X2=1)=P(X=1)=0.1,
p(η=4)=P(X2=4)=P(X=2)=0.1,
P(η=9)=P(X2=9)=P(X=3)=0.3,
P(η=16)=P(X2=16)=P(X=4)=0.3,
16
思维升华
(1)利用分布列中各概率之和为1可求参数的值,此时要注意检验,以保证每个概率值均为非负数.
(2)求随机变量在某个范围内的概率时,根据分布列,将所求范围内各随机变量对应的概率相加即可,其依据是互斥事件的概率加法公式.
设随机变量X的分布列为P(X=)=ak(k=1,2,3,4,5).
(1)求a;
(2)求P(X≥);
(3)求P(<
X≤).
解
(1)由分布列的性质,得P(X=)+P(X=)+P(X=)+P(X=)+P(X=1)=a+2a+3a+4a+5a=1,所以a=.
(2)P(X≥)=P(X=)+P(X=)+P(X=1)=3×
+4×
+5×
=.
(3)P(<
X≤)=P(X=)+P(X=)+P(X=)=++==.
题型二 离散型随机变量的分布列的求法
命题点1 与排列组合有关的分布列的求法
例2 (2015·
重庆改编)端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列.
解
(1)令A表示事件“三种粽子各取到1个”,则由古典概型的概率计算公式有P(A)==.
(2)X的所有可能值为0,1,2,且
P(X=0)==,P(X=1)==,
P(X=2)==.
综上知,X的分布列为
命题点2 与互斥事件有关的分布列的求法
例3 (2015·
安徽改编)已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:
元),求X的分布列.
解
(1)记“第一次检测出的是次品且第二次检测出的是正品”为事件A,
P(A)==.
(2)X的可能取值为200,300,400.
P(X=200)==,
P(X=300)==,
P(X=400)=1-P(X=200)-P(X=300)
=1--=.
故X的分布列为
200
300
400
命题点3 与独立事件(或独立重复试验)有关的分布列的求法
例4 (2016·
蚌埠模拟)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列.
解 用A表示“甲在4局以内(含4局)赢得比赛”,Ak表示“第k局甲获胜”,Bk表示“第k局乙获胜”.
则P(Ak)=,P(Bk)=,k=1,2,3,4,5.
(1)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)
=P(A1)P(A2)+P(B1)P(A2)P(A3)+P(A1)P(B2)·
P(A3)P(A4)
=2+×
2+×
×
2=.
(2)X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)
=P(A1)P(A2)+P(B1)P(B2)=,
P(X=3)=P(B1A2A3)+P(A1B2B3)
=P(B1)P(A2)P(A3)+P(A1)P(B2)P(B3)=,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)
=P(A1)P(B2)P(A3)P(A4)+P(B1)P(A2)P(B3)·
P(B4)=,
P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=.
思维升华 求离散型随机变量X的分布列的步骤:
(1)理解X的意义,写出X可能取的全部值;
(2)求X取每个值的概率;
(3)写出X的分布列.
求离散型随机变量的分布列的关键是求随机变量所取值对应的概率,在求解时,要注意应用计数原理、古典概型等知识.
(2016·
湖北部分重点中学第一次联考)连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为6分;
若k=2,则你的得分为4分;
若k=3,则你的得分为2分;
若抛掷三次还没找到你的幸运数字,则记0分,求得分ξ的分布列.
解
(1)设“连续抛掷3次骰子,和为6”为事件A,则它包含事件A1,A2,A3,其中A1:
三次恰好均为2;
A2:
三次中恰好1,2,3各一次;
A3:
三次中有两次均为1,一次为4.
A1,A2,A3为互斥事件,则
P(A)=P(A1)+P(A2)+P(A3)=C()3+C·
·
C·
+C()2·
(2)由已知得ξ的可能取值为6,4,2,0,
P(ξ=6)=,P(ξ=4)=()2+2×
C×
=,
P(ξ=2)=,P(ξ=0)=1---=.
故ξ的分布列为
ξ
6
题型三 超几何分布
例5 (2017·
济南质检)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;
在35微克/立方米~75微克/立方米之间空气质量为二级;
在75微克/立方米以上空气质量为超标.
从某自然保护区2016年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
PM2.5日均值(微克/立方米)
[25,35]
(35,45]
(45,55]
(55,65]
(65,75]
(75,85]
频数
(1)从这10天的PM2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列.
解
(1)记“从10天的PM2.5日均值监测数据中,随机抽出3天,恰有一天空气质量达到一级”为事件A,
则P(A)==.
(2)依据条件,ξ服从超几何分布,其中N=10,M=3,n=3,且随机变量ξ的可能取值为0,1,2,3.
P(ξ=k)=(k=0,1,2,3).
∴P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==,
P(ξ=3)==.
思维升华
(1)超几何分布的两个特点
①超几何分布是不放回抽样问题;
②随机变量为抽到的某类个体的个数.
(2)超几何分布的应用条件
①两类不同的物品(或人、事);
②已知各类对象的个数;
③从中抽取若干个个体.
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动.(每位同学被选到的可能性相同)
(1)求选出的3名同学来自互不相同学院的概率;
(2)设X为选出的3名同学中女同学的人数,求随机变量X的分布列.
解
(1)设“选出的3名同学来自互不相同的学院”为事件A,
故选出的3名同学来自互不相同学院的概率为.
(2)随机变量X的所有可能取值为0,1,2,3.
P(X=k)=(k=0,1,2,3).
∴P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
故随机变量X的分布列是
17.离散型随机变量的分布列
典例 某射手有5发子弹,射击一次命中概率为0.9.如果命中就停止射击,否则一直到子弹用尽,求耗用子弹数ξ的分布列.
错解展示
现场纠错
解 P(ξ=1)=0.9,
P(ξ=2)=0.1×
0.9=0.09,
P(ξ=3)=0.1×
0.1×
0.9=0.009,
P(ξ=4)=0.13×
0.9=0.0009,
P(ξ=5)=0.14=0.0001.
∴ξ的分布列为
0.9
0.09
0.009
0.0009
0.0001
纠错心得
(1)随机变量的分布列,要弄清变量的取值,还要清楚变量的每个取值对应的事件及其概率.
(2)验证随机变量的概率和是否为1.
1.(2016·
太原模拟)某射手射击所得环数X的分布列为
8
10
0.02
0.04
0.06
0.28
0.29
0.22
则此射手“射击一次命中环数大于7”的概率为( )
A.0.28B.0.88C.0.79D.0.51
解析 根据X的分布列知,所求概率为0.28+0.29+0.22=0.79.
2.(2016·
岳阳模拟)设X是一个离散型随机变量,其分布列为
1-2q
A.1B.1±
C.1-D.1+
解析 由题意知
即解得q=1-.
3.(2016·
郑州模拟)已知随机变量X的分布列为P(X=i)=(i=1,2,3,4),则P(2<
X≤4)等于( )
A.B.C.D.
答案 B
解析 由分布列的性质知,
+++=1,
则a=5,
∴P(2<
X≤4)=P(X=3)+P(X=4)=+=.
4.(2016·
湖北孝感汉川期末)设随机变量ξ的分布列为P(ξ=i)=a()i,i=1,2,3,则实数a的值为( )
A.1B.C.D.
答案 D
解析 ∵随机变量ξ的分布列为P(ξ=i)=a()i,i=1,2,3,
∴a[+()2+()3]=1,
解得a=.故选D.
5.(2017·
武汉调研)从装有3个白球,4个红球的箱子中,随机取出3个球,则恰好是2个白球,1个红球的概率是( )
解析 如果将白球视为合格品,红球视为不合格品,则这是一个超几何分布问题,故所求概率为P==.
6.(2017·
长沙月考)一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取出了X个白球,下列概率等于的是( )
A.P(X=3)B.P(X≥2)
C.P(X≤3)D.P(X=2)
解析 由超几何分布知P(X=2)=.
7.甲、乙两队在一次对抗赛的某一轮中有3个抢答题,比赛规定:
对于每一个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分);
若X是甲队在该轮比赛获胜时的得分(分数高者胜),则X的所有可能取值是________.
答案 -1,0,1,2,3
解析 X=-1,甲抢到一题但答错了,而乙抢到了两个题目都答错了,
X=0,甲没抢到题,乙抢到题目答错至少2个题或甲抢到2题,但答时一对一错,而乙答错一个题目,
X=1,甲抢到1题且答对,乙抢到2题且至少答错1题或甲抢到3题,且1错2对,
X=2,甲抢到2题均答对,
X=3,甲抢到3题均答对.
8.随机变量X的分布列如下:
a
b
c
其中a,b,c成等差数列,则P(|X|=1)=________,公差d的取值范围是________.
答案 [-,]
解析 ∵a,b,c成等差数列,∴2b=a+c.
又a+b+c=1,∴b=,
∴P(|X|=1)=a+c=.
又a=-d,c=+d,
根据分布列的性质,得0≤-d≤,0≤+d≤,
∴-≤d≤.
9.设离散型随机变量X的分布列为
若随机变量Y=|X-2|,则P(Y=2)=________.
答案 0.5
解析 由分布列的性质,知
0.2+0.1+0.1+0.3+m=1,∴m=0.3.
由Y=2,即|X-2|=2,得X=4或X=0,
∴P(Y=2)=P(X=4或X=0)
=P(X=4)+P(X=0)
=0.3+0.2=0.5.
10.袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量ξ,则P(ξ≤6)=________.
解析 P(ξ≤6)=P(取到3只红球1只黑球)+P(取到4只红球)=+=.
11.(2015·
山东改编)若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:
若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;
若能被5整除,但不能被10整除,得-1分;
若能被10整除,得1分.
(1)写出所有个位数字是5的“三位递增数”;
(2)若甲参加活动,求甲得分X的分布列.
解
(1)个位数是5的“三位递增数”有125,135,145,235,245,345.
(2)由题意知,全部“三位递增数”的个数为C=84,
随机变量X的取值为0,-1,1,因此
P(X=0)==,
P(X=-1)==,
P(X=1)=1--=.
所以X的分布列为