光学工程课后答案复习过程Word下载.docx
《光学工程课后答案复习过程Word下载.docx》由会员分享,可在线阅读,更多相关《光学工程课后答案复习过程Word下载.docx(53页珍藏版)》请在冰豆网上搜索。
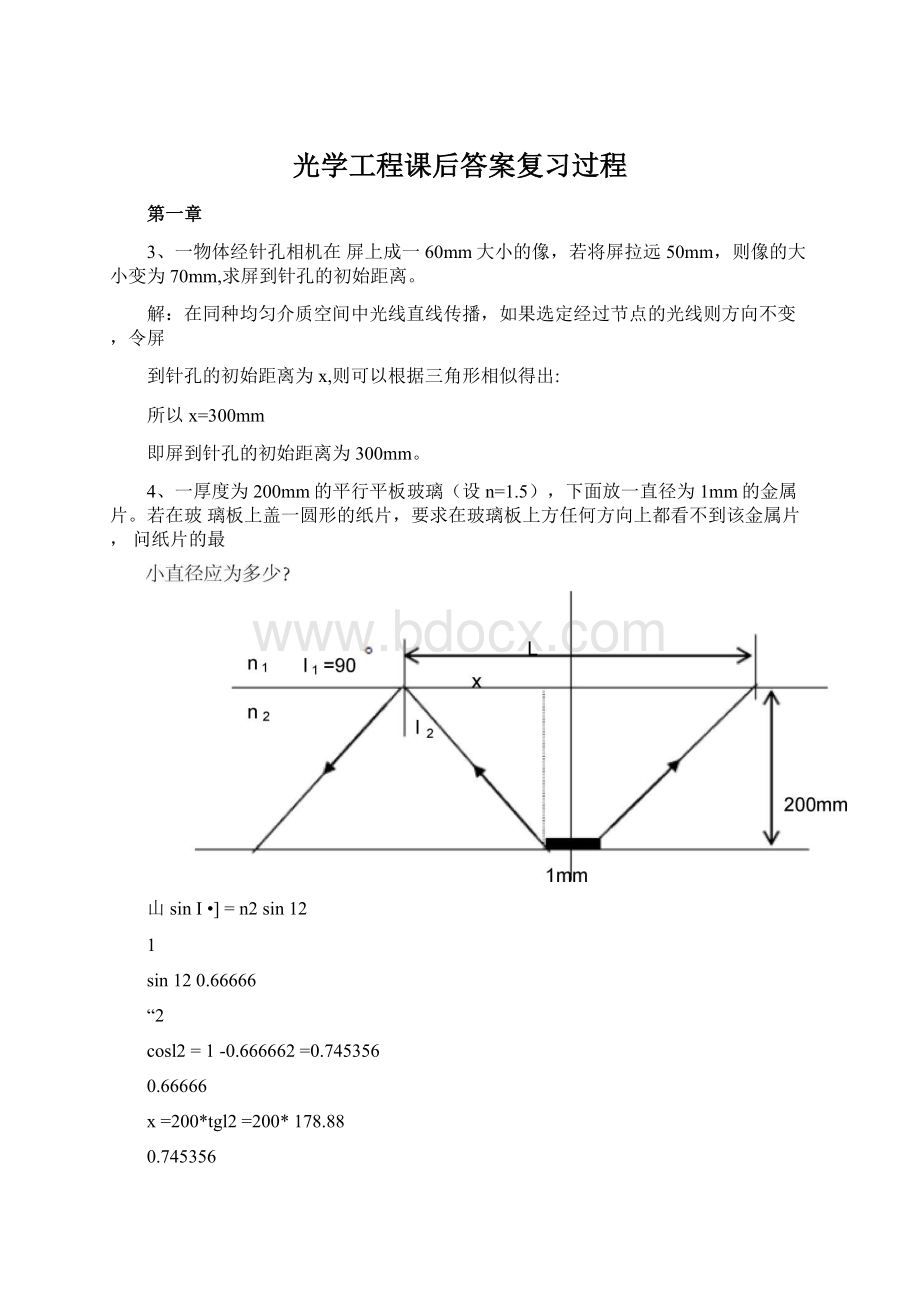
于看
1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?
如果在水中观察,
到的气泡又在何处?
设一个气泡在中心处,另一个在第二面和中心之间。
(1)从第一面向第二面看
1门半就气泡:
y-y"
得到!
r=8o
r=200
中心气泡,---=
r1
r
11.51-15
得至!
1:
r=-200
r-200
-200
1/2半径处气泡*
I5
-—
1-1,5得到,^--400
>
*«
11丄严亠1U«
]]
-300
-200倚王*
(2)从第二面向第面看
(3)在水中
19、
0=10得到:
⑴1H平行光先经第一面成像,以・2=业
I'
1r
口-丄得到;
4300
I1a100
即物经第一面成傢于平面处.
对于平面,=0得到厂=D,即像沟其本身.
即焦面处发出的光经第一面成像于无穷远处,为平行光出射,
(3)当入射高度为Mmin时;
M
sinZ'
=—sinJ
W^U+J-V
L=29?
398
Z*=r(l+
sinU*
20、一球面镜半径r=-100mm,求=0,-0.1,-0.2,-1,1,5,10时的
物距和象距。
21、
物体位于半径为r的凹面镜前什么位置时,可分别得到:
放大
4倍的实像,当大4
倍的虚像、缩小4倍的实像和缩小4倍的虚像?
(2)同理,
r=-10D
咋5。
/=450
(1)放大4倍的实像
5-Y
8
(2)放大四倍虚像
同理,得到:
3-T
2
(3)缩小四倍实|像
第二章
(4)缩小
四倍虚像
作图法分别对以下物距
一:
:
,_2f,_f,_f/2,0,f/2,f,二,求像平面的位置。
1.f'
0
el=0
A
<
A'
TF
B
B'
fI=f/2=-f'
/2
(g)l二f—f'
(h)l=2f
(i)l-二
2.f'
:
(e)l=0
(g)i=f
2、已知照相物镜的焦距f'
=75mm被摄景物位于(以F点为坐标原点)
x二-二,_10m,-8m,-6m,_4m,-2m,处,试求照相底片应分别放在离物镜的像方焦面多远
的地方。
(1)x=-X,xx'
=ff'
得到:
x'
=0
(2)x'
=0.5625
(3)x'
=0.703
(4)x
'
=0.937
(5)x'
=1.4
(6)x'
=2.81
解:
F
H
上
-f>
x
弋f'
>
、
-1丄
上|
w干
r
系统位于空气中,f'
=-f
--10
由已知条件:
f'
(-f)x=1140
「(-1)x=7200
解得:
f=600mm-60mm
4、已知一个透镜把物体放大-3冃投影到屏幕上,当透镜向物体移近18mm时,物体将被放
大-4*,试求透镜的焦距,并用图解法校核之。
11
方法
1—
l1
—
I2/
2一一
l2
-h-」2:
18=•
1/11—1/h=1/f'
1/12-1/12=1/f'
--311--3I2-18]①
12--412②
11=12-18③
1/1;
—1/14=1/12-1/12④
将①②③代入④中得12二―270mml2=-1080mm
=216mm
方法二:
-一L=_3
1-2二-丄=-4=f--216mm
X2
x2-x1=18
II
方法三:
亍=—=n】j=(-3)(-4)=12
lxn
-x1x2
f
4=1
f=x=216mm
.:
=1218--216
1-20
由3Lr解得:
=SO=/Lf!
、=604l2
p-p=y-•解得;
Z=240
fI1i(
=y-=-1»
=-80,—-—-—r*解得:
-40
6、有一正薄透镜对某一物成倒立的实像,
则所得像与物同大小,求该正透镜组的焦距。
l'
1
由已知得:
「二丄二-丄
112
I2
-h“2100
/
-I1曉>
、
宀
由高斯公式:
丄—丄1丄
l1l1I2|2
解得:
=100mm
00mm
€-l2鼻
乂I2了
J丿
7、希望得到一个对无限远成像的长焦距物镜,焦距=1200mm由物镜顶点到像面的距离L=700
mm由系统最后一面到像平面的距离(工作距)为丿山、®
,按最简单结构的薄透镜
系统考虑,求系统结构,并画出光路图。
③d=
=L-l\-700-400
④T.
=Al-yr)=f.=400
由①②③④得^'
-430,/'
--240,d=300
9、已知一透镜口-工00mm,r2--300mm,d=50mm,n=1.5,求其焦距,光焦度,基点位置。
已知「1-_200mm,r2--300mm,d=50mm,n=1.5
求:
\基点位置。
=1/f'
=(n_1)(二i_(n一1)d—-0.69m,n
-_1440mm
If=f'
(1—匸1d:
t)--1560mm
n
n—1s
If--f'
(1证)=1360mm
n-1
lH=-f'
()盯--120mm
lH=f'
(-1)d--80mm
叱
-rx)+
-■1440mm
10、一薄透镜组焦距为100mm和另一焦距为50mm的薄透镜组合,其组合焦距仍为100mm问两薄透镜的相对位置。
JX=50又r一半
/=100
得Id=100ffLni
:
、A=^50=(if^^1+//=d^lOO^SO
第三章
1•人照镜子时,要想看到自己的全身,问镜子要多长?
人离镜子的距离有没有关系?
镜子的高度为1/2人身高,和前后距离无关。
2、有一双面镜系统,光线平行于其中一个平面镜入射,经两次反射后,出射光线与另一平面镜平行,问两平面镜的夹角为多少?
M2M3//OA.MiNi_M2M3又l;
=Ti:
=|2-丨2
同理:
二=l;
—liM1M2M3中(I;
一丨2)(I;
-丨1)=180
■•-60
答:
a角等于60。
3、如图3-4所示,设平行光管物镜L的焦距f'
=1000mm顶杆离光轴的距离a=10mm如
果推动顶杆使平面镜倾斜,物镜焦点F的自准直象相对于F产生了y=2mm勺位移,问平
面镜的倾角为多少?
顶杆的移动量为多少?
-==―—1■
———――__==二二-
y=2fL
2x0.001rad
21000:
x二a)-100.001=0.01mm
图3-4
4、一光学系统由一透镜和平面镜组成,如图3-29所示。
平面镜MM与透镜光轴垂直交于D点,
透镜前方离平面镜600mn有一物体AB经透镜和平面镜后,所成虚像A'
B'
至平面
的距离为150mm且像高为物高的一半,试分析透镜焦距的正负,确定透镜的位置和
焦距,并画出光路图。
B」
I
i
D
SI
-L
L1
Br
150■
600
图3-29习题4图
由于平面镜性质可得A'
B'
及其位置在平面镜前150mn处
AB为虚像,AB为实像
AIA
贝=—L-L=600-150=450
2L2
解得L=-300L^150
111
又-—=f=150mm
L'
Lf'
透镜焦距为100mm
5、如图3-30所示,焦距为f'
=120mnt勺透镜后有一厚度为d=60mrm勺平行平板,其折射
率n=1.5。
当平行平板绕O点旋转时,像点在像平面内上下移动,试求移动量△y'
与
旋转角$的关系,并画出关系曲线。
如果像点移动允许有0.02mm勺非线形度,试求$
允许的最大值。
图3-3@°
习题5图
120解:
cosI1
d二DE
d
sin(l1-IJrsin(h-IJ
cos11
由图可知|1
sinI1二
sin11
cos11=
1sin2
d(sinI1COSI1'
cosI1
sin
n2_sin2'
■
-cos11sin11)
dcoshsinI1
cosli
cos11、
dsinl,1—)
ncos11
d'
'
d'
OB1「d1=OB1sin(■-IJ:
sin(■-11)
cosI1cos11
sin二nsin11
d1
cos■
-sin2■
当平行板转过0角时
OD1
sin(90-I-i)cosI-i
dsin(|--sin|;
)
cos11
cos(、亠:
;
))
n2_sin2(:
、亠匚)
(sin11cosIcos11sinIJcosl1
cos11,
dsinIJi「)=dsin(、亠•)(i
ncosl1
,'
'
、…,几、cos®
+°
)sin(⑷+°
)sin豹cose
d討-d2=d[sin(,)sin,
Jn2—sin2(⑷十$)Jn2—sin2⑷
13、.如图3-33所示,光线以45角入射到平面镜上反射后通过折射率n=1.5163,顶角为4
的光楔。
若使入射光线与最后的出射光线成90,试确定平面镜所应转动的方向和角度值。
图3-33习题13图
在.:
O,NO2中O1NO2=180「-176
nsin./o1O2N二sin:
-
o
sin40
O1O2N=arcsin2636787
1.5163
NOQ2=1.3632
sinv-nsin1.3632
.v-2.067
60
1.0336
平面镜顺时针旋转1.0336即可使入射光线与出射光线成90
第四章
1、设照相物镜的焦距等于75mm底片尺寸为55*55卿炖,求该照相物镜的最大视场角等于多少?
55^+55a
~2x75
第六章
7、.设计一双胶合消色差望远物镜,-一…宀,采用冕牌玻璃K9(;
*丨’丨「,
)和火石玻璃F2(.-I;
I:
,亡-‘丿),若正透镜半径「-■"
求:
正负透镜的焦距及三个球面的曲率半径。
企十色■(]
0L|轨
MJ36V
a
E=-44rx=44
池=(%-1耳--”
=>
©
=1425
叭=0.023566
=
A=424
化=0.013566
/'
i=73
第七章
1、•一个人近视程度是-2D(屈光度),调节范围是8D,求:
(1)远点距离;
(2)其近点距离;
(3)配戴100度近视镜,求该镜的焦距;
(4)戴上该近视镜后,求看清的远点距离;
5)戴上该近视镜后,求看清的近点距离。
①R2
lr
(1/m)
lr--0.5m
2A=R-PA=8DR=—2D
•••P=R-A=-2-8=-10D
11
lp0.1m
pP10
3D=—•-f--1m
厂
4R=R-D=-1D
l^-1m
5
R=-1D
A二R-PA=8D
P^R-A=-9D
lP0.11m
9
2、一放大镜焦距/=25mm,通光孔径°
=1滋切,眼睛距放大镜为50mm像距离眼
睛在明视距离250mm渐晕系数K=50%试求:
(1)视觉放大率;
(2)线视场;
(3)物体的位置。
(1)r=
O)
(3)
250
500力
500x9
5x50
200
50mm,像距离眼
eye
f--200
2、一放大镜焦距f'
=25mm,通光孔径D=18mm,眼睛距放大镜为
睛在明视距离250mm,渐晕系数为k=50%,试求
(1)视觉放大率;
物体的位置。
K=50%
①r②2y③I
PJD解:
①】可
25
50
=101-2=9
②由K=50%可得:
tg・H
2p・
I80.18
2*50
tg■
0.18
--tg0.02
ytg■
yD
•y=Dtg=250*0.02=5mm
2y=10mm
方法二:
tg•=0.18
y=250*tg•=45mm
I=-200mmfe=250mm
二:
.I=-22.2mm
-9X
=y_
y
③D=P-1
111
F"
T"
T
I—P-D=50-250--200mm
2y=10mm
——=
-200I25
I=-22.22mm
5、有一生物显微镜,物镜数值孔径
NA=0.5,物体大小2y=0.4mm,照明灯丝面积
12x1灯丝到物面的距离100mm采用临界照明,求聚光镜焦距和通
光孔径。
灯丝战像干物面友卜
视场光阑决定了物面大小,而物面又决定了照明的大小
二0.4
NA二料sm汎=0.5sin«
•0.5=
Di2
san嚣二tana——:
r-j=toor04』
1^=25
11.2P
/=-75
7、一开普勒望远镜,五经焦距f°
200mm,目镜的焦距为f©
=25mm,物方视场角2■=8,
渐晕系数K=50%,为了使目镜通光孔径D=23.7mm,在物镜后焦平面上放一场镜,试:
(1)求场镜焦距;
(2)若该场镜是平面在前的平凸薄透镜,折射率n=1.5,求其球面的曲率半径。
hZ0.5*Ds
l=164.1mm
孔阑
o*tg4=200*
丨丨f
=+
f场164.1200
f场=9.14mm
②丨冷「20.011
其中I-:
n=1.5
90.14
2=0.011
”•]=0
nnn'
llr
代入求得:
11.51-1.5
90.14:
r--45mm
第九章
2、在玻璃中传播的一个线偏振光可以表示Ev=0,Ez=0,Ex=10cos論015(——t),
y0.65c
试求
(1)光的频率和波长;
(2)玻璃的折射率。
(1d=50,由折射定律02=sin~*(niSin®
)=30.7e
n2
sin(羽_v2)sin(t•v2)
--0.335,「p
tg(“1^2)
tg(“e)
=0.057
由反射系数有AJ^rsA=「0.335人=「0.335代ApJrpAp=0.057A
■,合振幅与入射面的夹角tga=A/=a=—80.33。
⑵同理r
s--0.421心--0.042
宀arctg(丄)=84.3ap'
11、一个光学系统由两片分离透镜组成,两透镜的折射率分别为1.5和1.7,求此系统的
反射光能损失。
如透镜表面镀上曾透膜,使表面反射比降为0.01,问此系统的光能损失又
为多少?
设光束以接近正入射通过各反射面。
解
此系统有4个反射面,设光束正入射条件下,各面反射率为
1.5
R3=R4=0.067
.光能损失为(初始为I0)
.=1-R11-R21-R31-R4二0.802,损失20%
若反射比降为0.01,贝y=(1—0.01$=0.96,损失4%
13、线偏振光在玻璃-空气界面上发生全反射,线偏振光的方位角:
=45度,问线偏振光
以多大角度入射才能使反射光的s波和p波的相位差等于45度,设玻璃折射率n=1.5。
sin2冃
2「cos2^(sin21-n2)
tgr
全反射时,s波与P波相位差为■:
.,且dcos^Jsin2色
tg厂'
sin4
20i4222
1tg—sin-1nsin冇n=0
将n,:
=45代入有sin2冃=0.6483或0.5842
哥=53.63或49.85,而化=arcsin41.81
.上述答案均可
第十章
2、在杨氏实验中,两小孔距离为1mm观察屏离小孔的距离为50cm,当用一片折射率为
1.58的透明薄片贴住其中一个小孔时(见图11-17),发现屏上的条纹系统移动了0.5
场面,试决定试件厚度。
图11-47习题2图
设厚度为h,则前后光程差为=n-1h
h=1.7210^mm
7、在等倾干涉实验中,若照明光波的波长园=600nm,平板的厚度h=2mm,折射
率门=1.5,其下表面涂上某种高折射率介质(nh>
1.5),问
(1)在反射光方向观
到的圆条纹中心是暗还是亮?
(2)由中心向外计算,第10个亮纹的半径是多少?
(观
望远镜物镜的焦距为20cm)(3)第10个亮环处的条纹间距是多少?
(1):
no:
n:
nH,二光在两板反射时均产生半波损失,对应的光程差为
.■■:
=2nh=21.50.002=0.006m
•••中心条纹的干涉级数为
△6"
06
-10
为整数,所以中心为一亮纹
(2)由中心向外,第N个亮纹的角半径为g
半径为r10=fv10=0.067200mm=13.4mm
(3)第十个亮纹处的条纹角间距为
•Ton3.358103rad
102%h
•间距为.计10=f厶弓0=0.67mm
9、在等倾干涉实验中,若平板的厚度和折射率分别是h=3mm和n=1.5,望远镜的视场角
为60,光的波长卑450nm,问通过望远镜能够看到几个亮纹?
设有N个亮纹,中心级次
2nh—
21.5310;
N<
12.68
•可看到12条亮纹
第一章习题
1、已知真空中的光速c=3m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石