四边形复习导学案.doc
《四边形复习导学案.doc》由会员分享,可在线阅读,更多相关《四边形复习导学案.doc(6页珍藏版)》请在冰豆网上搜索。
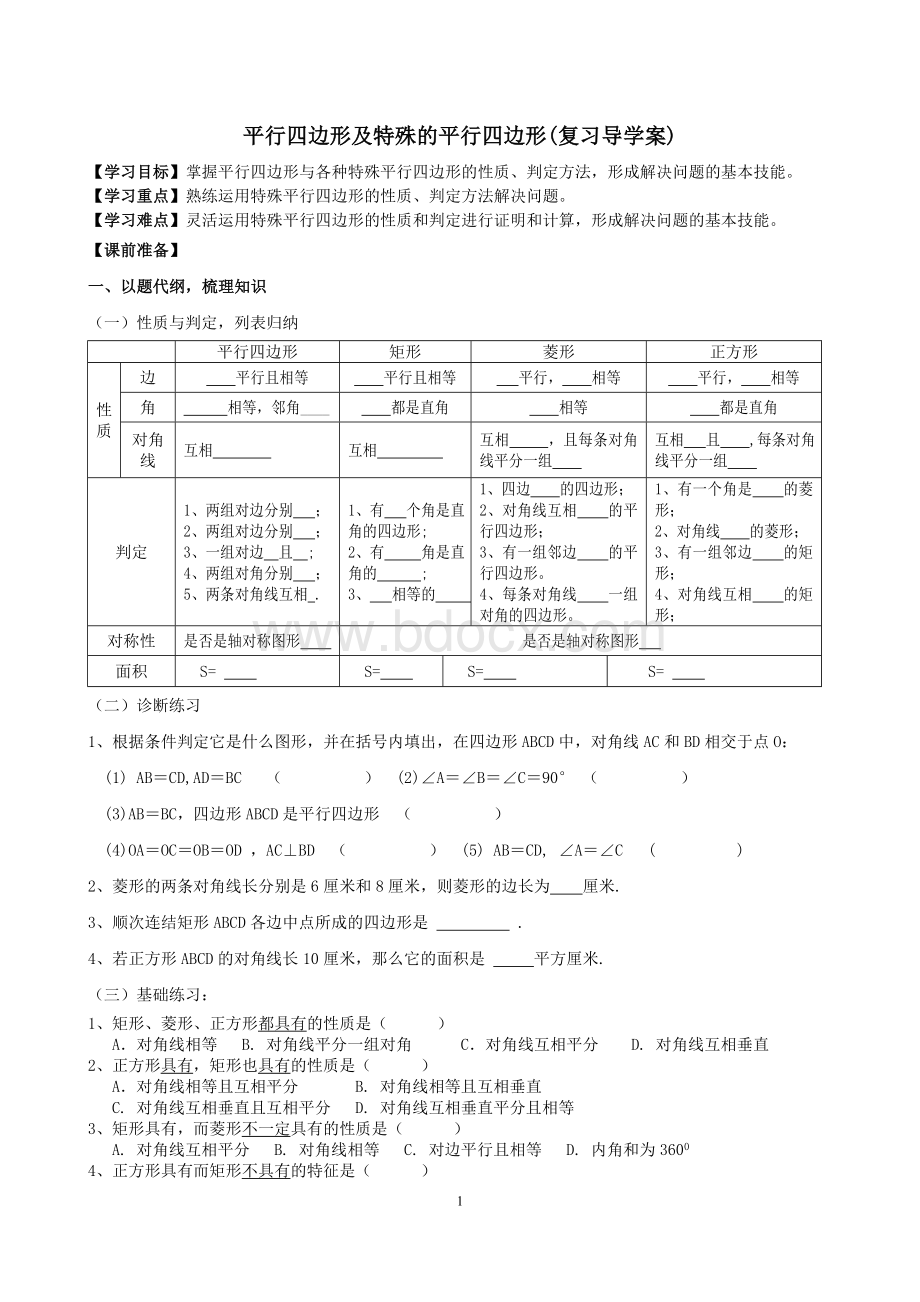
平行四边形及特殊的平行四边形(复习导学案)
【学习目标】掌握平行四边形与各种特殊平行四边形的性质、判定方法,形成解决问题的基本技能。
【学习重点】熟练运用特殊平行四边形的性质、判定方法解决问题。
【学习难点】灵活运用特殊平行四边形的性质和判定进行证明和计算,形成解决问题的基本技能。
【课前准备】
一、以题代纲,梳理知识
(一)性质与判定,列表归纳
平行四边形
矩形
菱形
正方形
性
质
边
平行且相等
平行且相等
平行,相等
平行,相等
角
相等,邻角____
都是直角
相等
都是直角
对角线
互相
互相
互相,且每条对角线平分一组
互相且,每条对角线平分一组
判定
1、两组对边分别;
2、两组对边分别;
3、一组对边且;
4、两组对角分别;
5、两条对角线互相.
1、有个角是直角的四边形;
2、有角是直角的;
3、相等的.
1、四边的四边形;
2、对角线互相的平行四边形;
3、有一组邻边的平行四边形。
4、每条对角线一组对角的四边形。
1、有一个角是的菱形;
2、对角线的菱形;
3、有一组邻边的矩形;
4、对角线互相的矩形;
对称性
是否是轴对称图形
是否是轴对称图形
面积
S=
S=
S=
S=
(二)诊断练习
1、根据条件判定它是什么图形,并在括号内填出,在四边形ABCD中,对角线AC和BD相交于点O:
(1)AB=CD,AD=BC()
(2)∠A=∠B=∠C=90°()
(3)AB=BC,四边形ABCD是平行四边形()
(4)OA=OC=OB=OD,AC⊥BD()(5)AB=CD,∠A=∠C()
2、菱形的两条对角线长分别是6厘米和8厘米,则菱形的边长为厘米.
3、顺次连结矩形ABCD各边中点所成的四边形是.
4、若正方形ABCD的对角线长10厘米,那么它的面积是平方厘米.
(三)基础练习:
1、矩形、菱形、正方形都具有的性质是( )
A.对角线相等B.对角线平分一组对角C.对角线互相平分 D.对角线互相垂直
2、正方形具有,矩形也具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直
C.对角线互相垂直且互相平分 D.对角线互相垂直平分且相等
3、矩形具有,而菱形不一定具有的性质是( )
A.对角线互相平分B.对角线相等C.对边平行且相等 D.内角和为3600
4、正方形具有而矩形不具有的特征是( )
A.内角和为3600 B.四个角都是直角C.两组对边分别相等D.对角线平分对角
二、典例精析,查漏补缺
A
B
C
D
O
E
F
【例题1】已知如图:
□ABCD的对角线AC、BD交于点O,EF过点O与
AB、CD分别交于点E、F.求证:
OE=OF.
A
B
D
C
O
H
G
变式1
变式1.在例1中,若改为过A作AH⊥BC,垂足为H,连结HO并延长交AD于G,连结GC,则四边形AHCG是什么四边形?
请证明,
A
B
C
D
O
G
H
变式2
变式2.在例1中,若作GH⊥BD,GH分别交AD、BC于G、H,则四边形BGDH是什么四边形?
为什么?
O
B
H
C
A
G
D
变式3
变式3.在例1中,若将“□ABCD”改为“矩形ABCD”,GH分别交AD、BC于G、H,则四边形BGDH是什么四边形?
若AB=6,BC=8,你能求出GH的长吗?
B
A
D
C
F
E
【例题2】已知:
如图,在正方形ABCD,E是BC边上一点,F是CD的中点,
且AE=DC+CE.求证:
AF平分∠DAE.
二、中考题选编
1.如图1,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 _______
2.如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为___________.
3.如图2,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是.
4.如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
5.如图所示,已知E为□ABCD中DC延长线上的一点,且CE=DC,连接AE,分别交BC和BD于点F和点G,连接AC交BD于点O,连接OF,试说明:
AB=2OF.
6.如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:
BE=DF.
7.如图,在□ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF
(1)求证:
四边形CEDF是平行四边形.
(2)①当AE=___________cm时,四边形CEDF是矩形.
②当AE=___________cm时,四边形CEDF是菱形.
8.如图,四边形ABCD、四边形BEFG均为正方形,连接AG,CE.
求证:
(1)AG=CE.
(2)AG⊥CE.
9.已知:
如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:
△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:
AB=_________时,四边形MENF是正方形(只写结论,不需证明)
三.课堂小结:
集合表示,突出关系()
()
()
()
()
四边形
平行四边形
矩形
菱形
正方形
(在横线上写出满足条件)
四.课后作业(试卷)
A
E
B
C
D
A
E
B
C
D
1.如图,在□ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=_______________.
A
B
C
D
E
(例1)(变式1)(变式2)
变式1如图,在□ABCD中,是边上的中点,若则平行四边形的周长是_________.
变式2如图,在平行四边形ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数是.
2.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,
PE⊥AC,PF⊥BD于F,则PE+PF的值为________.
B
E
F
C
A
D
B
E
F
C
A
D
3.如图,在□ABCD中,E、F分别是对角线BD上两点,且BE=DF,要判别四边形AECF是平行四边形,你能找出几种方法?
D
C
A
B
E
F
(变式一)(变式二)
变式一:
如图,在□ABCD中,E、F分别是对角线BD上两点,且AE∥CF,求证:
(1)△ABE≌△CDF;
(2)∠EAF=∠ECF
变式二:
如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:
BE与DF有怎样的位置关系和数量关系?
并对你的猜想加以证明.
4.如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:
ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,
连接DM,试判断四边形BMDF的形状,并说明理由.
5.如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:
EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?
并证明你的结论.
6.已知正方形ABCD,ME⊥AC,MF⊥BD,垂足分别为E、F
(1)M是AB上的点,若对角线AC=12cm,求ME+MF的长。
(2)当M点运动到何处时,四边形MFOE的面积最大?
7.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:
四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
8.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:
∠ADB=∠CDB;
(2)若∠ADC=90°,求证:
四边形MPND是正方形.
6