北师大版七年级几何习题经典测试提文档格式.docx

北师大版七年级几何习题经典测试提文档格式.docx

《北师大版七年级几何习题经典测试提文档格式.docx》由会员分享，可在线阅读，更多相关《北师大版七年级几何习题经典测试提文档格式.docx（14页珍藏版）》请在冰豆网上搜索。

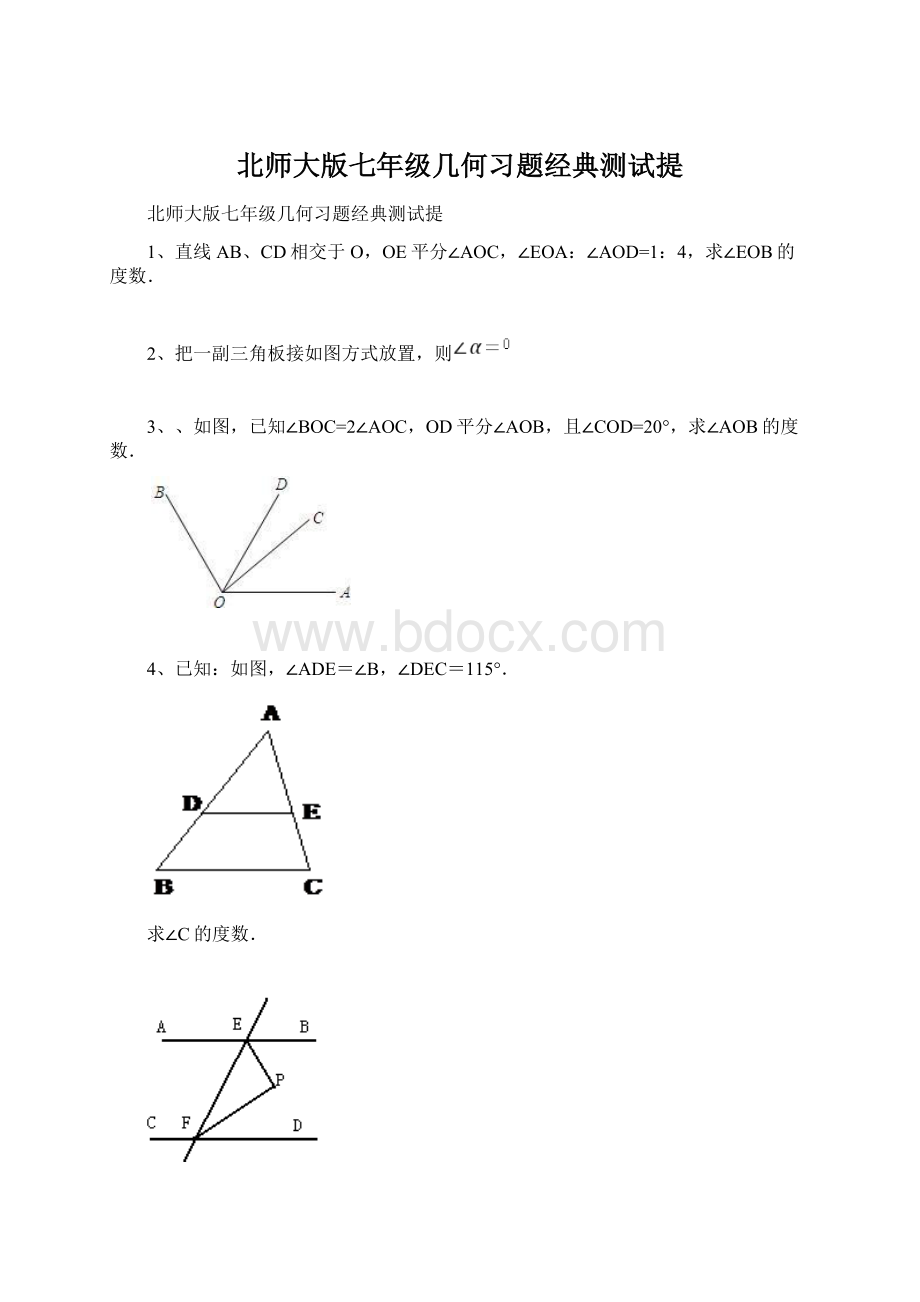
8、如图△ABC中，AD,AE分别是△ABC的高和角平分线，∠B=42°

∠DAE=14°

.求∠CAD和∠C的度数。

9、如图，已知：

DE∥BC，CD是∠ACB的平分线，∠B＝70°

，∠ACB＝50°

，求∠EDC和∠BDC的度数．

10、如图AB∥CD，∠NCM＝90°

，∠NCB＝30°

，CM平分∠BCE，求∠B的大小．

11、如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=500,求∠DEG的度数.

12、如图，OA=OB，OC=OD，∠O=50°

，∠D=35°

，求∠AEC的度数。

13、如图，在△ABC中，∠C=90°

，∠BAC的平分线AD交BC于点D，且AB=7，CD=2．求△ABD的面积。

14、如图，△ABC中，AB=ACD在BC上,∠BAD=30°

在AC上取点E，使AE=AD,

求∠EDC的度数

15、现有等腰三角形纸片,如果能从一个角的顶点出发,将原纸片一次剪开成两块等腰三角形纸片,问此时的等腰三角形的顶角的度数?

16、P为等边△ABC所在平面上一点,且△PAB,△PBC,△PCA都是等腰三角形,这样的点P有_______个.

17、如图，已知：

E、F分别是AB和CD上的点，DE、AF分别交BC于G、H，

A=

D，

1=

2，求证：

B=

C．

18、如图，已知：

AB//CD，求证：

B+

D+

BED=

19、如图，在△ABC中，AB=AC，D是BC的中点，E在AD上，BE=CE吗？

说明你的理由.（8分）

20、如图，已知AB∥CD，EF交AB,CD于G,H,GM,HN分别平分

，试说明GM∥HN.

21、 

已知：

如图，AD∥BC，∠BAD=∠BCD，求证：

AB∥CD。

22、、已知，如图，AC∥BD，∠C=90°

，BC=BD，AC=BE．那么AB、DE有何关系？

为什么？

23、以直角三角形ABC的两直角边AB、BC为一边，分别向外作等边三角形△ABE和等边△BCF，连接EF、EC。

试说明：

（1）EF＝EC；

（2）EB⊥CF.

24、如图，AB=AC,AD⊥BC于点D,AD=AE,AB平分

DAE交DE于点F.

请你写出图中五对全等三角形，并选取其中一对加以证明．

25、如图：

在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截CG=AB，连结AD、AG。

求证：

（1）AD=AG，

（2）AD⊥AG。

26、AB∥CD，直线a交AB、CD分别于点E、F，点M在EF上，P是直线CD上的一个动点，（点P不与F重合）

（1）当点P在射线FC上移动时，

∠FMP+∠FPM=∠AEF成立吗？

请说明理由。

（2）当点P在射线FD上移动时，

∠FMP+∠FPM与∠AEF有什么关系？

并说明你的理由。

27、如图△ABC中，∠ACB＝90°

，AC＝BC，AE是BC边上的中线，过点C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．

　　求证：

①AE＝CD．②若AC＝12cm，求BD的长．

28、两个大小不同的等腰三角

形三角板如图如示放置，图2是由它抽象

出的几何图形，点B、C、E在同一条直

线上，连接DC．

⑴请找出图2中的全等三角形，并给予证

明（说明：

结论中不得含有未标识的字母）；

⑵证明：

DC⊥BE．

29、如图，已知在△ABC中，∠ABC＝45°

，H是高AD和BE的交点．

①求证：

BH＝AC

②现将原图中的∠BAC改为钝角，题设条件不变，请你

按题设要求在钝角三角形ABC中画出该题的图形．

③在②的条件下，结论BH＝AC还成立吗？

请证明，

若不成立，请说明理由．

30、如图：

AD是△ABC中∠BAC的平分线，过AD的中点E作EF⊥AD交BC的延长线于F，连结AF。

∠B=∠CAF。

31、如图：

AD是△ABC的中线，DE⊥AC于E，DF⊥AB于F，且BF=CE，点P是AD上一点，PM⊥AC于M，PN⊥AB于N。

求证：

（1）DE=DF，

（2）PM=PN。

32、如图，已知△ACB、△FCD都是等腰直角三角形，且C在AD上，AF的延长线与BD交于E，请你在图中找出一对全等三角形，并写出它们全等的过程.

33、如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．

（1）求证：

△FGC≌△EBC；

（2）若AB=8，AD=4，求四边形ECGF（阴影部分）的面积．

34、如图，已知：

在

中，

，AC=BC，BD平分

CBA，

于E，求证：

AD+DE=BE．

35、如图，已知BE⊥AC，CF⊥AB，垂足分别为E，F，BE，CF相交于点D，若BD=CD．

AD平分∠BAC。

36、如图

（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点；

研究

（1）：

若沿直线DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；

研究

（2）：

若折成图2的形状，猜想∠BDA′，∠CEA′和∠A关系，并说明理由；

研究（3）：

若折成图3的形状，猜想∠BDA′，∠CEA′和∠A的关系，并说明理由．

图1图2图3

37、已知：

如图，AB＝DC，AC＝BD，AC、BD相交于点E，过E点作EF∥BC，交CD于F，

（1）根据给出的条件，请找出与△ABC全等的三角形？

并说明理由；

（2）EF平分∠DEC吗？

38、如图，在△ABC中，

90°

，AB＝AC，D是BC边上一点，EC⊥BC，且EC＝BD，F是DE的中点，请判断AF与DE是否垂直，为什么？

39、如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE，BD和CE相交于点F，若△ABC不动，将△ADE绕点A任意旋转一个角度．

（1）如图

（1），若∠BAC=∠DAE=90°

，判断线段BD与CE的关系，并说明理由；

（2）如图

（2），若∠BAC=∠DAE=60°

，求∠BFC的度数；

（3）如图（3），若∠BAC=∠DAE=α，直接写出∠BFC的度数．（不需说明理由）

40、如图1，已知：

△ABC中，AB=AC，∠BAC=90°

，AE是过A的一条直线，且B、C在AE的两侧，BD⊥AE于D，CE⊥AE于E．

（1）△ABD与△CAE全等吗？

BD与AE、AD与CE相等吗？

（2）BD、DE、CE之间有什么样的等量关系（写出关系式即可）

（3）若直线AE绕A点旋转，如图2，其它条件不变，那么BD与DE、CE的关系如何？

说明理由。

41、如图①，△ABC是等边三角形，过点C作CD//AB，且CD＝AB，连接AD。

（1）判断△ACD的形状，并说明理由；

（2）若再延长BC到点E，作等边△AEF，连接DF，即得图②，试说明CE与DF相等的理由并求

的度数。

42、如图，△ABC与△ADE都是等边三角形，连结BD、CE交点记为点F．

（1）BD与CE相等吗？

请说明理由．

（2）你能求出BD与CE的夹角∠BFC的度数吗？

43、已知：

△ABC为等边三角形，M是BC延长线上一点，直角三角尺的一条直角边经过点A，且60º

角的顶点E在BC上滑动，（点E不与点B、C重合），斜边与∠ACM的平分线CF交于点F

（1）如图

（1）当点E在BC边的中点位置时

猜想AE与EF满足的数量关系是。

（提示：

过E作EN//AC交AB于N）

猜想BE和CF满足的数量关系是　　　　　

请证明你的上述猜想（4分）

（2）如图

（2）当点E在BC边的任意位置时：

　此时AE和EF有怎样的数量关系，并说明你的理由？

44、如图，已知△ABC三边长相等，和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．在图

（1）中，点P是边BC的中点，由S△ABP+S△ACP=S△ABC得，

可得

又因为h3=0，所以：

图

（2）~（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．

（1）请探究：

图

（2）~（5）中，h1、h2、h3、h之间的关系；

（直接写出结论）

⑵⑶⑷⑸

（2）说明图

（2）所得结论为什么是正确的；

（3）说明图（5）所得结论为什么是正确的．