数学实验报告赛车跑道Word下载.docx
《数学实验报告赛车跑道Word下载.docx》由会员分享,可在线阅读,更多相关《数学实验报告赛车跑道Word下载.docx(14页珍藏版)》请在冰豆网上搜索。
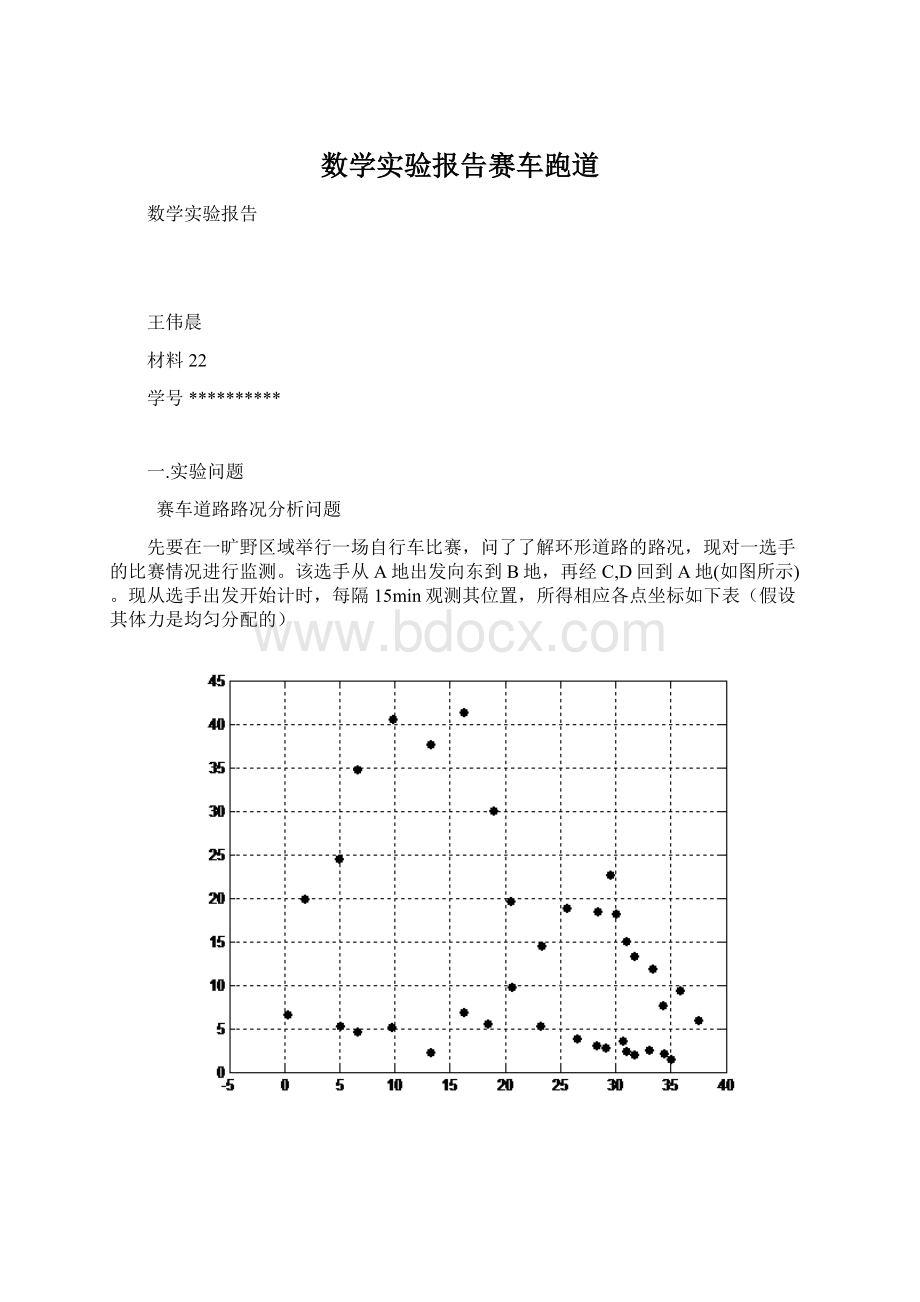
26.49
纵坐标Y
6.66
5.28
4.68
5.19
2.34
6.94
5.55
9.86
3.87
28.23
29.1
30.65
30.92
31.67
33.03
34.35
35.01
37.5
3.04
2.88
3.68
20.38
2.06
2.58
2.16
1.45
6
由D到C到B的位置坐标(单位千米)
横坐标
x
1.8
4.90
6.51
9.73
13.18
16.20
18.92
20.50
23.23
25.56
19.89
24.52
34.82
40.54
37.67
41.38
30.00
19.68
14.56
18.86
28.31
29.45
33.31
34.23
35.81
18.55
22.66
18.28
15.06
13.42
11.86
7.68
9.45
假设:
1车道几乎是在平地上,但有三种路况(根据平均速度v(km/h)大致区分)
;
平整沙土路(v>
30),坑洼碎石路(12<
v<
30),松软泥泞路(v<
12);
2车道是一条连续的可用光滑曲线来近似表示的闭合路线;
3选手的速度是连续变化的。
求解:
1模拟比赛车道的曲线和选手的速度曲线;
2估计车道的长度和所谓区域的面积;
3分析车道上相关路段的路面状况(在车道上用不同的颜色标记出来);
4对参加比赛的选手提出合理化建议。
二问题分析
由给定的一系列x,y坐标采用插值法,获得一条严格通过个数据点的曲线。
共有三种插值法;
1多项式插值
对于已知的n个数据点
…;
(
),可唯一的确定一条n-1次多项式y=
+
+…+
令
则所求的多项式系数为方程组Ax=y的解。
故x=
利用命令y0=polyval(p,x0)可求得多项式函数任一点的函数值。
该种方法得到的曲线容易出现“龙格现象”,故一般不用该方法模拟曲线。
2分段线性插值
在每一个子区间上利用一次多项式分段线性插值,几何图形上的表示为相邻两个数据点之间用直线相连。
在数据点个数较多时,他们之间的距离较小,利用线性插值就较为精确。
其线性插值命令为y0=interpl(x,y,x0)
3三次样条插值
该种方法是利用某些光滑的,变化平缓的曲线来拟和数据点。
常用一个三次多项式,来对相继数据点之间的各段建模,使其满足相邻的三次多项式在节点处的1阶2阶导数都相等,这样就可以确定内部各段的3次多项式,且该三次多项式在节点处的斜率和曲率是连续的。
该插值方法的命令格式为yo=spline(x,y,xo)
要求比赛车道的曲线和选手的速度曲线利用以上三种插值方法即可。
三.程序的设计
首先分析A→B的赛道情况
1描点
clf;
clear
x=[0.24.966.559.7113.1716.2318.3620.5323.1526.4928.2329.130.6530.9231.6733.0334.3535.0137.5];
y=[6.665.284.685.192.346.945.559.865.283.873.042.883.682.382.062.582.161.456];
plot(x,y,'
k.'
'
markersize'
15);
axis([-540045]);
grid
2绘图
利用三次样条插值
grid;
holdon
t=-5:
0.5:
40;
u=spline(x,y,t);
plot(t,u)
s=trapz(x,y);
l=sqrt(diff(x).^2+diff(y).^2);
L=sum(l);
fprintf('
s=%.2f,L=%.3f\n'
s,L)
s=177.20,L=51.832
再分析A→D→C→B的赛道情况
x=[0.21.84.906.519.7313.1816.2018.9220.5023.2325.5628.3129.4530.0030.9231.6733.3134.2335.8137.5];
y=[6.6619.8924.5234.8240.5437.6741.3830.0019.6814.5618.8618.5522.6618.2815.0613.4211.867.689.456];
s=903.96,L=107.350
最后在分析选手由A→B→C→D→A的运动情况
x=[0.24.966.559.7113.1716.2318.3620.5323.1526.4928.2329.130.6530.9231.6733.0334.3535.0137.51.84.906.519.7313.1816.2018.9220.5023.2325.5628.3129.4530.0030.9231.6733.3134.2335.8137.5];
y=[6.665.284.685.192.346.945.559.865.283.873.042.883.682.382.062.582.161.45619.8924.5234.8240.5437.6741.3830.0019.6814.5618.8618.5522.6618.2815.0613.4211.867.689.456];
holdon
x1=[0.21.84.906.519.7313.1816.2018.9220.5023.2325.5628.3129.4530.0030.9231.6733.3134.2335.8137.5];
y1=[6.6619.8924.5234.8240.5437.6741.3830.0019.6814.5618.8618.5522.6618.2815.0613.4211.867.689.456];
plot(x1,y1,'
t1=-5:
u1=spline(x1,y1,t);
plot(t1,u1)
速度曲线
clear;
clc
v1=[19.82406.797812.803617.930622.099310.173719.301821.105814.50177.71133.53846.97715.31103.26175.82415.54083.877520.7471];
v2=[53.305622.287941.700326.256217.950819.135146.802241.761023.209419.562811.069717.060717.657613.39547.21349.053817.12029.490515.3668];
a=size(v2);
b=size(v1);
t=0:
0.25:
(0.25*(b
(2)+a
(2)-1));
fori=1:
a
(2)
v1(b
(2)+i)=v2(a
(2)+1-i);
end
plot(t,v1,'
axis([09.30056]);
k=0:
0.1:
(0.25*(b
(2)+a
(2)));
u=spline(t,v1,k);
plot(k,u)
路面状况曲线
b=size(x1);
a=size(x);
a
(2)-1
v1(i)=sqrt((x(i+1)-x(i))^2+(y(i+1)-y(i))^2)/(15/60);
X=[x(i),x(i+1)];
Y=[y(i),y(i+1)];
holdon
ifv1(i)>
30
plot(X,Y,'
r-.'
linewidth'
3)
elseifv1(i)<
12
g-'
else
m--'
end
b
(2)-1
v2(i)=sqrt((x1(i+1)-x1(i))^2+(y1(i+1)-y1(i))^2)/(15/60);
X=[x1(i),x1(i+1)];
Y=[y1(i),y1(i+1)];
ifv2(i)>
elseifv2(i)<
四.问题的求解结果与结论
1比赛车道曲线
选手的速度曲线
2.车道长度为159.182km
车道曲线所围区域的面积为726.76
3.车道上的路面状况为;
4.建议:
参赛选手应注意体力的分配与自行车的保养,根据不同的路面状况选择相应的骑车速度,能够以最短的时间完成比赛.
五.实验的总结与体会
这次实验题目比较大也比较难,需要分段分析路面状况,同时也要根据具体情况选择相应的拟合方法,涉及的程序较多,难度比较大.在画比赛车道曲线时,发现当把A→B→C→D→A的所有点都放在一起编程时Matlab无法画出曲线因此必须分段来画才能画出整个车道的曲线。
在画选手的速度曲线时,由于题目的已知条件有限,不能根据已求得的比赛车道曲线通过求该曲线的斜率得到。
更具题目可以知道每个15min就要观测一次选手的位置,因此可以用选手在这段时间所走的路程除以这段路程的时间就可以得到选手在这段路程的平均速度,根据这种方法共可以得到37个点,再采用以上的描点绘图方法,得到选手的速度曲线。
分析车道上相关路面状况时,要使用判断语句,应此使用了C++中相关知识。
在做数学实验时要仔细分析题目,对要使用的知识点有一个大概的了解,其次要综合利用各种知识不仅仅是Matlab中的相关知识其他学科中的知识也要学会观察进来。