湖北省黄冈市届高三数学一轮复习备考教学设计概率与统计说课文档Word格式.docx

湖北省黄冈市届高三数学一轮复习备考教学设计概率与统计说课文档Word格式.docx

《湖北省黄冈市届高三数学一轮复习备考教学设计概率与统计说课文档Word格式.docx》由会员分享，可在线阅读，更多相关《湖北省黄冈市届高三数学一轮复习备考教学设计概率与统计说课文档Word格式.docx（16页珍藏版）》请在冰豆网上搜索。

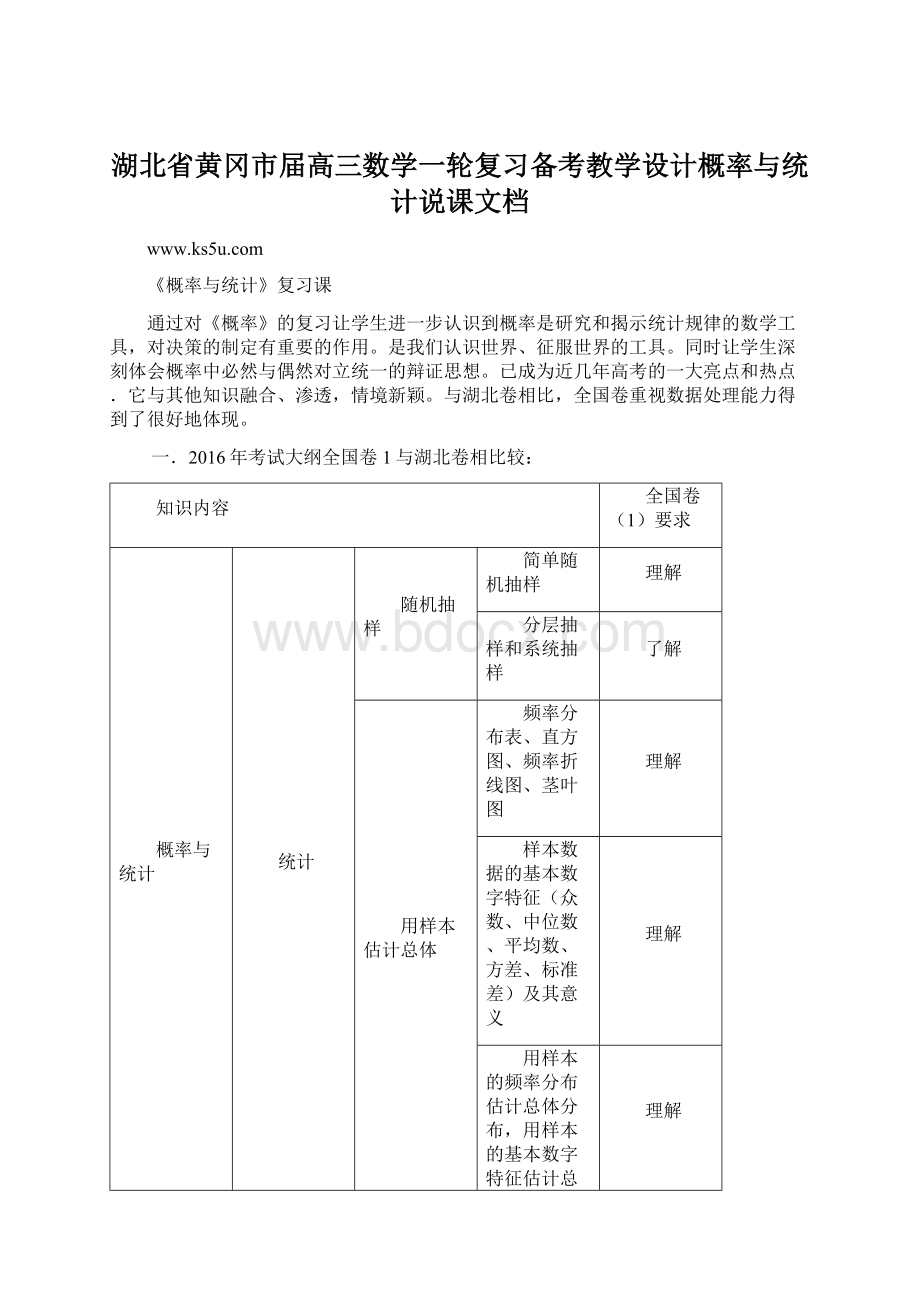
用样本的频率分布估计总体分布，用样本的基本数字特征估计总体的基本数字特征

变量的相关性

相关关系和散点图

最小二乘法

线性回归方程

概率

事件与概率

随机事件的关系与运算

随机事件的概率

两个互斥事件的概率加法公式

古典概型

计算一些随机事件所含的基本事件数及事件发生的概率（理科）

用列举法计算一些随机事件所含的基本事件数及事件发生的概率（文科）

随机数与几几何概型

随机数

几何概型

概率与统计（仅限理科）

取有限个值的离散型随机变量及其分布列

超几何分布

条件概率

事件的独立性

n次独立重复试验模型及二项分布

取有限个值的离散型随机变量均值、方差

正态分布

回归思想

独立性检验

对比前几年的的考试大纲，全国卷1变化非常小

二．近四年全国卷1中本专题的考试特点与命题规律：

全国理

难易程度

全国文

2016年

选择题4：

考查几何概型

易

选择题3：

考查古典概型及概率计算公式（列举法）

解答题19：

考查直方图，数字特征和分布列；

难

考查频率分布直方图；

2015年

考查独立重复试验；

互斥事件和概率公式

考查古典概型

（列举法）

考查非线性拟合；

线性回归方程求法；

利用回归方程进行预报预测；

2014年

选择题5：

考查古典概型，互斥事件，对立事件

中等

填空题13：

容易

解答题18：

考查直方图，数字特征和正态分布

考查直方图，

数字特征，

较易

2013年

考查抽样方法

考查条件概率，相互独立事件，互斥事件

难度较大

考查茎叶图，用样本的基本数字特征估计总体的基本数字特征

（1）题型与分值均不变

从近四年全国卷1看：

无论文理题型都稳定为一大一小两道题，分值17分，占比约11%。

（2）考查内容不变

这四年中仅有2013年的理数卷是小题考查统计（抽样方法），大题考查概率（条件概率）。

其余五卷均与之相反，都是小题考查概率，大题考查统计知识。

（3）密切联系教材，重视对基础知识和基本技能考查

试题通常是通过对常见题型进行改编，通过对基础知识的整合、变式和拓展，从而加工为立意高、情境新、设问巧的实际问题．

（4）重点考察本单元知识在实际生活中的应用

文科小题一般主要考查古典概型，难度较小。

解答题以对统计的考查为主，几乎所有的统计考点都有所涉及，应用性和开放性都越来越强，对学生的能力要求越来越高。

（5）试题的文字、数据和图形的信息量大

由此预计这些特点2017年依然会延续下去。

三．专题知识体系构建的方法与总体构思（复习计划）

1.指导思想

以基础知识为明线，数学思想作暗线，突出主线（解题方法，思维能力）

2．课时安排

本单元包括6讲和1个120分钟标准单元能力检测卷，每讲连课时训练一起2课时，试卷2课时，共需14课时完成．

3.单元知识体系

四．重点知识强化策略包括常见题型和解题方法，难点突破策略。

教学重点

1.基本概念和基本公式。

如等可能性事件的概率、互斥事件的概率、对立事件的概率、相互独立事件的概率、独立重复试验。

2.常见题型的解题方法。

如抽样方法，频率分布表和频率分布直方图，离散型随机变量分布列和数学期望、方差。

3.知识的应用。

如预测问题，决策问题等。

难点突破

1.事件之间的关系即确定概率类型

2.阅读图表，处理数据，运算求解

3.将实际问题转化为数学问题即建模

4.理解概率的或然与必然的思想本质

教法学法分析

采用“引导”“点拔”等教学方法，学生通过独立思考、自主解题、合作交流等学习方式，熟练知识，发展能力。

常见题型——概率

一盒中装有大小和质地均相同的12个小球，其中5个红球，4个黑球，2个白球，1个绿球，从中随机取出1球，求：

（1）取出的小球是红球或黑球的概率；

（2）取出的小球是红球或黑球或白球的概率．

（1）当所求事件情况较复杂时，一般要分类计算，这就要用到互斥事件的概率加法公式或考虑其对立事件．

（2）当所求事件中含有“至少”“至多”或分类情况较多时，可考虑其对立事件．

如图，从A1（1，0，0），A2（2，0，0），B1（0，1，0），B2（0，2，0），C1（0，0，1），C2（0，0，2）这6个点中随机选取3个点．

（1）求这3点与原点O恰好是正三棱锥的四个顶点的概率；

（2）求这3点与原点O共面的概率．

解析：

从这6个点中随机选取3个点的所有可能结果是：

x轴上取2个点，有A1A2B1，A1A2B2，A1A2C1，A1A2C2，共4种；

y轴上取2个点，有B1B2A1，B1B2A2，B1B2C1，B1B2C2，共4种；

z轴上取2个点，有C1C2A1，C1C2A2，C1C2B1，C1C2B2，共4种；

所选取的3个点在不同坐标轴上，有A1B1C1，A1B1C2，A1B2C1，A1B2C2，A2B1C1，A2B1C2，A2B2C1，A2B2C2，共8种．

（1）有关古典概型的概率问题，关键是求出基本事件总数和事件A包含的基本事件数．

（2）在用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助于“树状图”列举．

例1：

如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆．在扇形OAB内随机取一点，则此点取自阴影部分的概率是（　　）

例2：

小明和小雪约了星期天下午在月牙塘公园见面，由于龙泉路最近在修路，可能会堵车小明说他大概4:

00—5:

00会到，小雪说这次她大概5:

00—6:

00就会到了，这次他们约定先到的等半个小时另一个还没来就可以先走，假设他们在自己估计时间内到达的可能性相等，问他们两个能相遇的概率有多大？

分析：

如果在一维坐标轴中表示他们相遇的可能性则种类太多，表达不清，又因为小明到达的时间在4点至5点间，小雪到达的时间在5点到6点间，属于两个变量的情形，所以我们采用二维的坐标系来构建这个题的数学模型。

设小明到达的时间为x，小雪到达时间为y，那么

约定先到的等半个小时另一个还没来就可以先走则他们两个要相遇需要满足

解：

设小明到达的时间为x，小雪到达时间为y，小明和小雪相遇为事件A

则

试验的全部结果所构成的区域为

事件A构成的区域为

由图可知

，则

所以小明和小雪相遇的概率为1/8

（1）当试验的结果构成的区域为长度、面积、体积、弧长、夹角等时，应考虑使用几何概型求解；

（2）利用几何概型求概率时，关键是试验的全部结果构成的区域和事件发生的区域的寻找，有时需要设出变量，在坐标系中表示所需要的区域．

（3）几何概型中约会问题利用二位坐标系来解决，是高考中的常考题型，不可忽视。

某校共有学生2000名，各年级男、女生人数如下表所示．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为（　　）

（1）解决此类题目首先要深刻理解各种抽样方法的特点和适用范围，如分层抽样，适用于数目较多且各部分之间具有明显差异的总体．

（2）系统抽样中编号的抽取和分层抽样中各层人数的确定是高考重点考查的内容．

某地区为了解70～80岁老人的日平均睡眠时间（单位：

h），随机选择了50位老人进行调查，下表是这50位老人日睡眠时间的频率分布表．

在上述统计数据的分析中，一部分计算见算法流程图，则输出的S的值是________．

（1）解决该类问题时应正确理解图表中各个量的意义，从图表中掌握信息是解决该类问题的关键．

（2）本题中S实际上是样本的近似平均数．我们可以根据频率分布表或频率分布直方图来大致求出样本的平均数，具体做法是，用频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和．

随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：

cm），获得身高数据的茎叶图如下图所示．

（1）根据茎叶图判断哪个班的平均身高较高；

（2）计算甲班的样本方差；

（3）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率．

解析：

（1）由茎叶图可知：

甲班身高集中于160～179cm之间，而乙班身高集中于170～180cm之间．因此乙班平均身高高于甲班．

（2）x＝（158＋162＋163＋168＋168＋170＋171＋179＋179＋182）÷

10＝170.

（1）本题考查了茎叶图的识图问题和平均数的计算，其中从茎叶图中读出数据是关键，为此，首先要弄清“茎”和“叶”分别代表什么．

（2）要熟练掌握众数、中位数、平均数、方差、标准差的计算方法．

（2014·

新课标Ⅱ卷）某地区2007年至2013年农村居民家庭纯收入y（单位：

千元）的数据如下表：

（1）求y关于t的线性回归方程；

（2）利用

（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入。

（1）正确作出散点图，由散点图可知两个变量是否具有线性相关关系，若具有线性相关关系，则可通过线性回归方程估计和预测变量的值．

（2）正确记忆求b，a的公式和准确地计算，是解题的保证．

五．训练试题的选择及其意图。

概率与统计六大易混易错点：

1、混淆“相互独立事件的概率”与“互斥事件的概率”而致误

2、混淆“条件概率”与“相互独立事件的概率”而致误

3、混淆“二项分布”与“超几何分布”而致误

4、忽视正态分布的图像而致误

5、线性回归方程的性质不熟练而致误

6、不理解独立性检验的思想而致误

针对这些易错点，结合学生实际（任教班级的学情），可以设置一些小题组，进行实战演练、强化训练，从而提高教学的针对性和有效性。

类型一“非等可能”与“等可能”混同

例1掷两枚骰子，求所得的点数之和为6的概率．

错解掷两枚骰子出现的点数之和2，3，4，…，12共11种基本事件，所以概率为P=

剖析以上11种基本事件不是等可能的，如点数和2只有（1，1），而点数之和为6有（1，5）、（2，4）、（3，3）、（4，2）、（5，1）共5种．事实上，掷两枚骰子共