初中数学七八九年级知识点和公式总结大全人版Word下载.docx

初中数学七八九年级知识点和公式总结大全人版Word下载.docx

《初中数学七八九年级知识点和公式总结大全人版Word下载.docx》由会员分享，可在线阅读，更多相关《初中数学七八九年级知识点和公式总结大全人版Word下载.docx（33页珍藏版）》请在冰豆网上搜索。

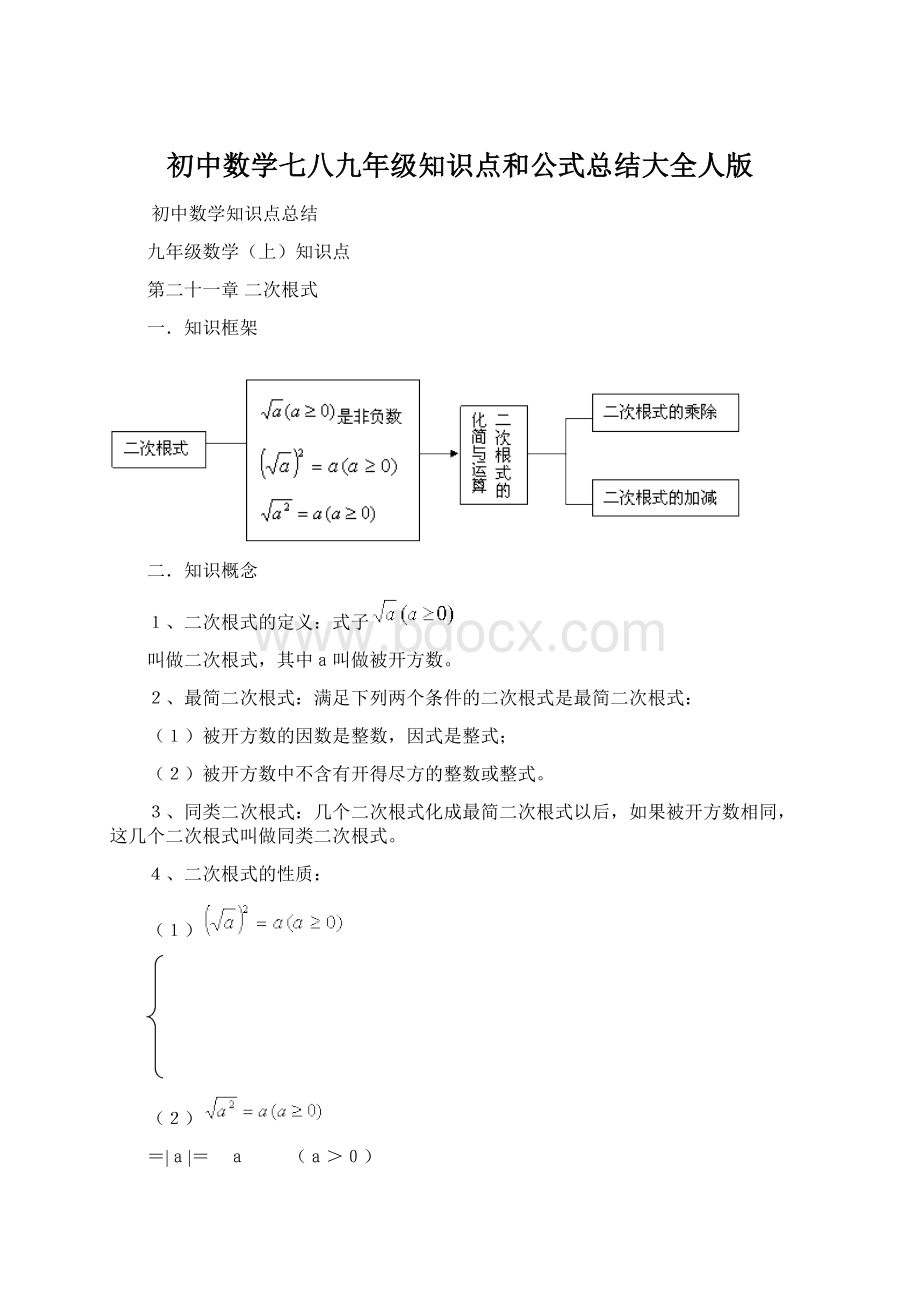
（ａ≥０，ｂ＞０）

５、二次根式的乘法：

＝

（ａ≥０，ｂ≥０）即两个二次根式相乘，根指数不变，被开方数相乘。

注意：

法则是由积的算数平方根的性质

（ａ≥０，ｂ≥０）反过来即得。

６、二次根式的除法：

法则是由商的算数平方根的性质

（ａ≥０，ｂ＞０）反过来得到的。

７、二次根式的加减：

二次根式相加减，先把各个二次根式化成最简二次根式，在合并同类二次根式，合并同类二次根式与合并同类项类似，将同类二次根式的“系数”相加减，被开方数和根指数不变。

二次根式加减混合运算的实质就是合并同类二次根式，不是同类二次根式不能合并。

８、二次根式的混合运算：

二次根式的混合运算顺序与实数的运算顺序一样，先乘方，后乘除，最后加减，有括号的先算括号内的。

在运算过程中，有理数（式）中的运算率及乘法公式在二次根式的运算中仍然适用。

９、比较两数大小的常用方法：

（１）平方法：

若ａ＞０，ｂ＞０，且ａ²

＞ｂ²

，则ａ＞ｂ；

（２）把跟号外的非负因式移到根号内，然后比较被开方数的大小。

第二十二章一元二次根式

一．知识框

二.知识概念

１.一元二次方程：

方程两边都是整式，只含有一个未知数（一元），并且未知数的最高次数是2（二次）的方程，叫做一元二次方程．

一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式ax2+bx+c=0（a≠0）．这种形式叫做一元二次方程的一般形式．其中ax2是二次项，a是二次项系数；

bx是一次项，b是一次项系数；

c是常数项．

２.一元二次方程的解法：

（1）运用开平方法解形如（x+m）2=n（n≥0）的方程；

领会降次──转化的数学思想．

（2）配方法：

将一元二次方程变形为（x+p）２=q的形式，如果q≥0，方程的根是x=-p±

√q；

如果q＜0,方程无实根．

（3）公式法：

将方程化为一般形式ax2+bx+c=0，当b2-4ac≥0时，将a、b、c代入式子x=

就得到方程的根．

第二十三章旋转

一.知识框架

1.旋转：

在平面内，将一个图形绕一个点按某个方向转动一个角度，这样的运动叫做图形的旋转。

这个定点叫做旋转中心，转动的角度叫做旋转角。

图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。

）

2.旋转对称图形：

把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角（旋转角小于0°

，大于360°

）。

3．中心对称图形与中心对称：

中心对称图形：

如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形。

中心对称：

如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称。

4.中心对称的性质：

（１）关于中心对称的两个图形是全等形。

（２）关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

（３）关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。

第二十四章圆

二．知识概念　　

1.圆：

平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

2.圆弧和弦：

圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，小于半圆的弧称为劣弧。

连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。

3.圆心角和圆周角：

顶点在圆心上的角叫做圆心角。

顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。

4.内心和外心：

过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心。

和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。

5.扇形：

在圆上，由两条半径和一段弧围成的图形叫做扇形。

6.圆锥侧面展开图是一个扇形。

这个扇形的半径称为圆锥的母线。

7.圆和点的位置关系：

以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；

P在⊙O上，PO＝r；

P在⊙O内，PO＜r。

8.直线与圆有3种位置关系：

无公共点为相离；

有两个公共点为相交,这条直线叫做圆的割线；

圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点。

9.两圆之间有5种位置关系：

无公共点的，一圆在另一圆之外叫外离，在之内叫内含；

有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；

有两个公共点的叫相交。

两圆圆心之间的距离叫做圆心距。

两圆的半径分别为R和r，且R≥r，圆心距为P：

外离P＞R+r；

外切P=R+r；

相交R-r＜P＜R+r；

内切P=R-r；

内含P＜R-r。

10.切线的判定方法：

经过半径外端点并且垂直于这条半径的直线是圆的切线。

11.切线的性质：

（1）经过切点垂直于这条半径的直线是圆的切线。

（2）经过切点垂直于切线的直线必经过圆心。

　　　　　（3）圆的切线垂直于经过切点的半径。

12.垂径定理：

垂直于弦的直径平分弦，并且平分弦所对的两条弧。

13.有关定理：

（１）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．

（２）在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．

（３）在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

（４）半圆（或直径）所对的圆周角是直角，90°

的圆周角所对的弦是直径．

14.圆的计算公式：

　（１）圆的周长C=2πr=πd；

　（２）圆的面积S=πr2;

　（３）扇形弧长l=nπr/180；

　（４）扇形面积S=π（R2-r2）；

　（５）圆锥侧面积S=πrl；

第二十五章概率

1．生活中的随机事件分为确定事件和不确定事件，确定事件又分为必然事件和不可能事件，其中必然事件发生的概率为1，即P（必然事件）=1；

不可能事件发生的概率为0,即P（不可能事件）=0；

如果A为不确定事件，那么0<

P（A）<

1

2．随机事件发生的可能性（概率）的计算方法：

（１）只涉及一步实验的随机事件发生的概率，如：

根据概率的大小与面积的关系，对一类概率模型进行的计算；

（２）通过列表法、列举法、树状图来计算涉及两步或两步以上实验的随机事件发生的概率．

九年级数学（下）知识点

第二十六章二次函数

二．.知识概念

1.定义：

一般地，自变量x和因变量y之间满足y=ax2+bx+c（a≠0，a、b、c为常数），则称y为x的二次函数。

2.二次函数的解析式三种形式。

一般式：

　y=ax2+bx+c（a≠0）

顶点式：

交点式：

3.二次函数y=ax2+bx+c（a≠0，a、b、c为常数）图像与性质

对称轴：

顶点坐标：

与y轴交点坐标（0，c）

4.增减性：

当a>

0时，对称轴左边，y随x增大而减小；

对称轴右边，y随x增大而增大；

当a<

0时，对称轴左边，y随x增大而增大；

对称轴右边，y随x增大而减小．

5.五点法画二次函数图像：

顶点、与x轴两个交点、与y轴交点及其对称点。

6.图像平移步骤

（1）配方

，确定顶点（h,k）

（2）对x轴左加右减；

对y轴上加下减

7.二次函数的对称性

二次函数是轴对称图形，若两个对称点的横坐标分别为x1,x2，那么对称轴

8.根据图像判断a,b,c的符号

（1）a——开口方向

（2）b——对称轴与a左同右异

9.二次函数与一元二次方程的关系

（１）抛物线y=ax2+bx+c与x轴交点的横坐标x1,x2是一元二次方程ax2+bx+c=0（a≠0）的根。

（２）抛物线y=ax2+bx+c，当y=0时，抛物线便转化为一元二次方程ax2+bx+c=0

（３）

>

0时，一元二次方程有两个不相等的实根，二次函数图像与x轴有两个交点；

=0时，一元二次方程有两个相等的实根，二次函数图像与x轴有一个交点；

<

0时，一元二次方程有不等的实根，二次函数图像与x轴没有交点

二次函数知识很容易与其它知识综合应用，而形成较为复杂的综合题目。

因此，以二次函数知识为主的综合性题目是中考的热点考题，往往以大题形式出现．教师在讲解本章内容时应注重培养学生数形结合的思想和独立思考问题的能力。

第二十七章相似

一．知识框架

二.知识概念：

1.相似三角形：

对应角相等，对应边成比例的两个三角形叫做相似三角形。

2.相似三角形的判定方法:

（１）根据定义判断：

对应边成比例，对应角相等；

（２）平行于三角形一边的直线（或两边的延长线）和其他两边相交,所构成的三角形与原三角形相似；

（３）如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似；

（４）如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似；

（５）如果两个三角形的三组对应边的比相等,那么这两个三角形相似；

3.直角三角形相似判定定理:

（１）斜边与一条直角边对应成比例的两直角三角形相似。

（２）直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

4.相似三角形的性质:

（１）相似三角形的一切对应线段（对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。

（２）相似三角形周长的比等于相似比。

（３）相似三角形面积的比等于相似比的平方。

第二十八章锐角三角函数

1.Rt△ABC中

（1）∠A的对边与斜边的比值是∠A的正弦，记作sinA＝

（2）∠A的邻边与斜边的比值是∠A的余弦，记作cosA＝

（3）∠A的对边与邻边的比值是∠A的正切，记作tanA＝

（4）∠A的邻边与对边的比值是∠A的余切，记作cota＝

2.特殊值的三角函数：

a

sina

cosa

tana

cota

30°

45°

60°

第二十九章投影与视图

知识框架

八年级数学（上）知识点

第十一章全等三角形

1.全等三角形：

大小和形状完全相同的两个三角形叫做全等三角形。

2．全等三角形的性质：

全等三角形的对应角相等、对应边相等。

3.三角形全等的判定公理及推论有：

（1）“边角边”简称“SAS”：

两边及其夹角对应相等，两三角形全等；

（2）“角边角”简称“ASA”：

两角及其夹边对应相等，两三角形全等；

（3）“边边边”简称“SSS”：

三组对应边相等，两三角形全等；

（