一次函数的应用三种题型.doc
《一次函数的应用三种题型.doc》由会员分享,可在线阅读,更多相关《一次函数的应用三种题型.doc(8页珍藏版)》请在冰豆网上搜索。
一次函数的应用
行程问题
k、b所表达的意义:
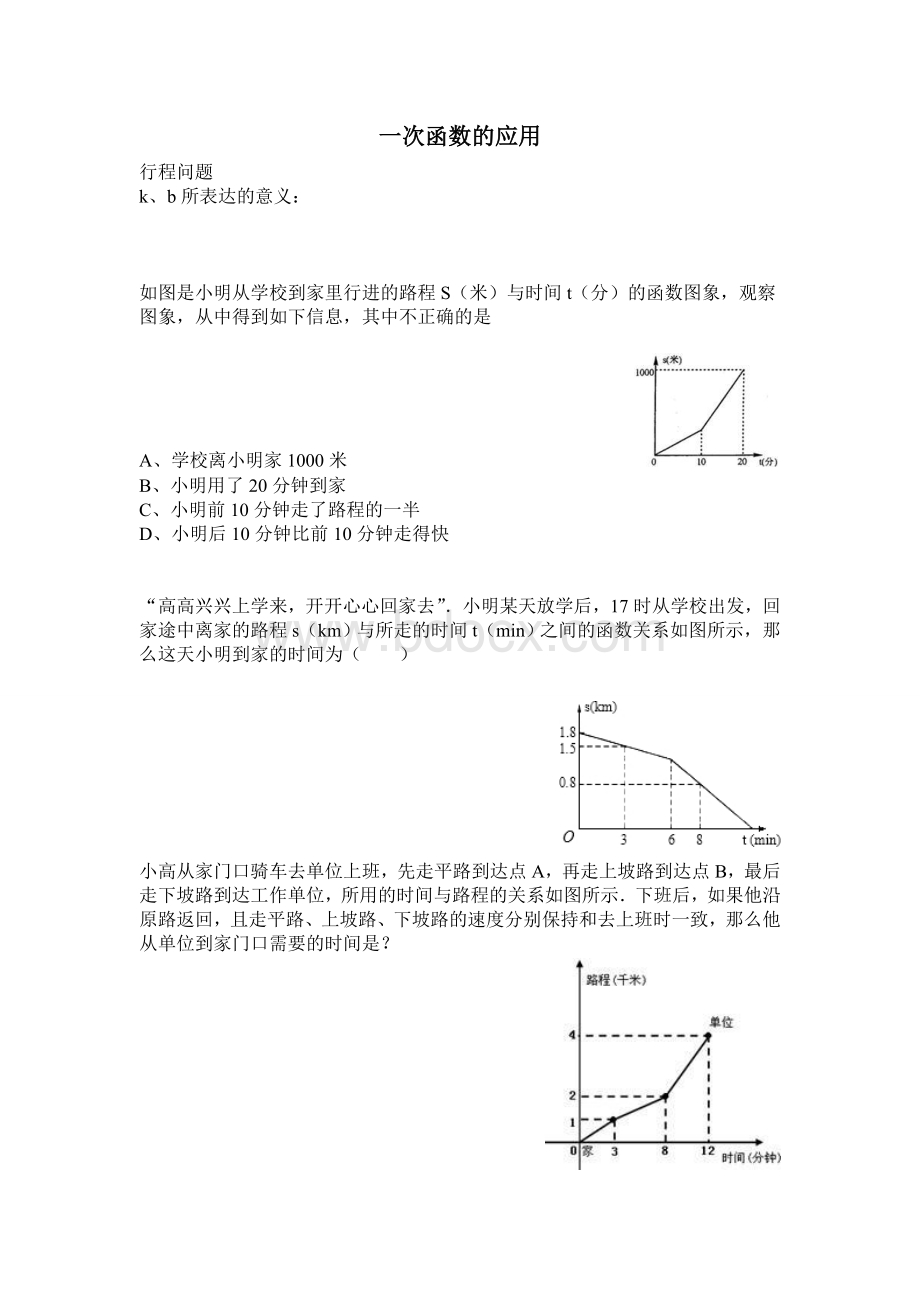
如图是小明从学校到家里行进的路程S(米)与时间t(分)的函数图象,观察图象,从中得到如下信息,其中不正确的是
A、学校离小明家1000米
B、小明用了20分钟到家
C、小明前10分钟走了路程的一半
D、小明后10分钟比前10分钟走得快
“高高兴兴上学来,开开心心回家去”.小明某天放学后,17时从学校出发,回家途中离家的路程s(km)与所走的时间t(min)之间的函数关系如图所示,那么这天小明到家的时间为( )
小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是?
追击问题
如图
(1),在同一直线,甲自A点开始追赶等速度前进的乙,且图
(2)表示两人距离与所经时间的线型关系.若乙的速率为每秒1.5公尺,则经过40秒,甲自A点移动多少公尺?
如图OB、AB分别表示甲、乙两名同学运动的一次函数图象,图中s和t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:
①甲让乙先跑12米;②甲的速度比乙快1.5米/秒;③8秒钟内,乙在甲前面;④8秒钟后,甲超过了乙,其中正确的说法是( )
为迎接2008年北京奥运会,某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。
如图,线段L1,L2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象。
根据图象,解答下列问题:
(1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;
(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学
快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.下图表示的是两车之问的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息.解答下列问题:
(1)直接写出快、慢两车的速度及A、B两站间的距离;
(2)求快车从B返回A站时,y与x之间的函数关系式;
(3)出发几小时,两车相距200千米?
请直接写出答案.
甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线、线段分别表示甲、乙两车所行路程(千米)与时间(小时)之间的函数关系对应的图象(线段表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
(1)求乙车所行路程与时间的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?
(写出解题过程)
A
O
D
P
B
F
G
E
y(千米)
x(小时)
480
6
8
10
2
4.5
有一个附有进水管和出水管的容器,在单位时间内的进水量和出水量分别一定.设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,得到容器内水量y(升)与时间x(分)之间的函数图象如图.若20分钟后只放水不进水,这时(x≧20时)y与x之间的函数关系式是
某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油过程中,设运输飞机的油箱余油量为Q1t,加油飞机的加油油箱余油量为Q2t,加油时间为tmin,Q1,Q2与t之间的函数图象如图所示,结合图象回答下列问题:
(1)加油飞机的加油油箱中装载了______吨油.
(2)将这些油全部加给运输飞机需______分钟.
(3)求加油过程中,运输飞机的余油量Q(t)与时间t(min)的函数关系式.
(4)运输飞机加完油后,以原速继续飞行,需10h到达目的地,油料是否够用
一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回.一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,立即返回(掉头时间忽略不计).已知轮船在静水中的速度是22千米/时,水流速度是2千米/时.下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度,逆流速度=船在静水中速度-水流速度)
(1)甲、乙两港口的距离是________千米;快艇在静水中的速度是_________千米;
(2)求轮船返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少.为缓解旱情,北方甲水库立即以管道运输的方式给予以支援下图是两水库的蓄水量y(万米3)与时间x(天)之间的函数图象.在单位时间内,甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计).通过分析图象回答下列问题:
(1)甲水库每天的放水量是多少万立方米?
(2)在第几天时甲水库输出的水开始注入乙水库?
此时乙水库的蓄水量为多少万立方米?
(3)求直线AD的解析式.
相遇问题
某中学九年级甲、乙两班商定举行一次远足活动,A、B两地相
y1
O
10
y/千米
x/小时
2
2.5
y2
距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发
匀速步行到A地。
两班同时出发,相向而行。
设步行时间为x小
时,甲、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x
的函数关系图像如图所示,根据图像解答下列问题:
(1)直接写出,y1、y2与x的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?
相遇时乙班离A地多少千米?
甲从P地前往Q地,乙从Q地前往P地.设甲离开P地的时间为t(小时),两人距离Q地的路程为S(千米),图中的线段分别表示S与t之间的函数关系.根据图象的信息,下列说法正确的序号是( )
①甲的速度是每小时80千米;②乙的速度是每小时50千米;
③乙比甲晚出发1小时;④甲比乙少用2.25小时到达目的地;⑤图中a的值等于6607.
邮递员小王从县城出发,骑自行车到A村投递,途中遇到县城中学的学生李明从A村步行返校.小王在A村完成投递工作后,返回县城途中又遇到李明,便用自行车载上李明,一起到达县城,结果小王比预计时间晚到1分钟.二人与县城间的距离(千米)和小王从县城出发后所用的时间(分)之间的函数关系如图,假设二人之间交流的时间忽略不计,求:
(1)小王和李明第一次相遇时,距县城多少千米?
请直接写出答案.
(2)小王从县城出发到返回县城所用的时间.
(3)李明从A村到县城共用多长时间?
工程问题
一件工作,甲、乙两人合做5小时后,甲被调走,剩余的部分由乙继续完成,设这件工作的全部工作量为1,工作量与工作时间之间的函数关系如图所示,那么甲、乙两人单独完成这件工作,下列说法正确的是
A、甲的效率高B、乙的效率高C、两人的效率相等D、两人的效率不能确定
甲乙两个工程队分别从A,B两村同时相向开始修筑公路,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,甲乙两个工程队修道路的长度y(米)与修筑时间x(天)之间的函数图象如图,则该公路的总长度为
利润问题
如图,反映了某公司的销售收入与销量的关系,反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入>成本)时,销售量必须
某加油站五月份营销一种油品的销售利润y(万元)与销售量x(万升)之间函数关系的图象如图中折线所示,该加油站截止到13日调价时的销售利润为4万元,截止至15日进油时的销售利润为5.5万元.
(销售利润=(售价-成本价)×销售量)
请你根据图象及加油站五月份该油品的所有销售记录提供的信息,解答下列问题:
(1)求销售量x为多少时,销售利润为4万元;
(2)分别求出线段AB与BC所对应的函数关系式;
(3)我们把销售每升油所获得的利润称为利润率,那么,在OA、AB、BC三段所表示的销售信息中,哪一段的利润率最大?
(直接写出答案)
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低元。
(1)填表(不需化简)
时间
第一个月
第二个月
清仓时
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
某经营世界著名品牌的总公司,在我市有甲、乙两家分公司,这两家公司都销售香水和护肤品.总公司现香水70瓶,护肤品30瓶,分配给甲、乙两家分公司,其中40瓶给甲公司,60瓶给乙公司,且都能卖完,两公司的利润(元)如下表.
(1)假设总公司分配给甲公司X瓶香水,求:
甲、乙两家公司的总利润W与X之间的函数关系式;
(2)在
(1)的条件下,甲公司的利润会不会比乙公司的利润高?
并说明理由;
每瓶香水利润
每瓶护肤品利润
甲公司
180
200
乙公司
160
150