七年级数学上学期第三章第六节探索规律PPT课件下载推荐.ppt

七年级数学上学期第三章第六节探索规律PPT课件下载推荐.ppt

《七年级数学上学期第三章第六节探索规律PPT课件下载推荐.ppt》由会员分享，可在线阅读，更多相关《七年级数学上学期第三章第六节探索规律PPT课件下载推荐.ppt（41页珍藏版）》请在冰豆网上搜索。

aa-7a+7

（2）

（2）竖列三个相邻数竖列三个相邻数下者比上者多下者比上者多7能用字母表示吗能用字母表示吗?

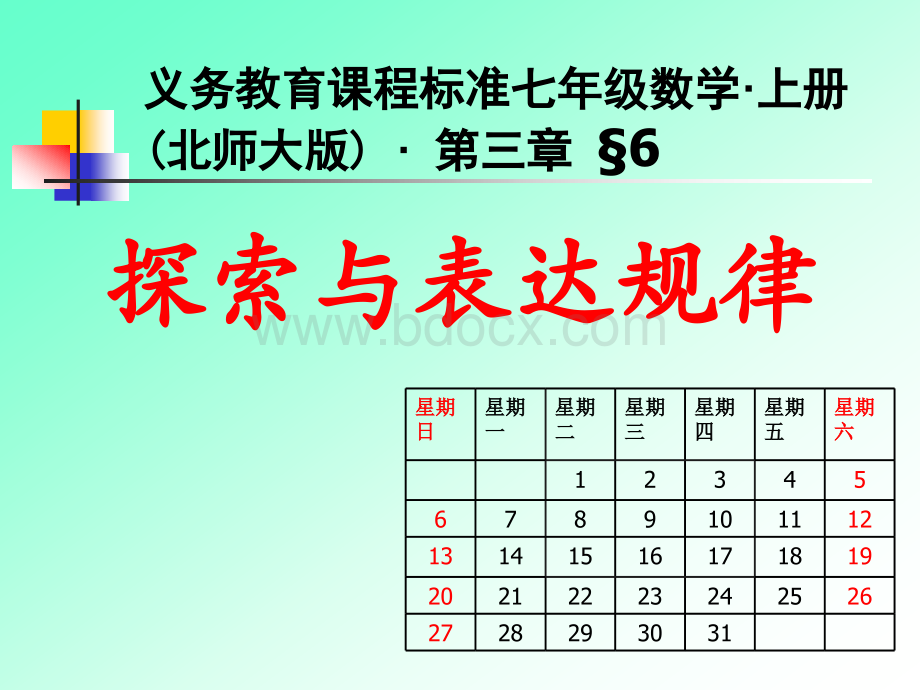
星期星期日日星期星期一一星期星期二二星期星期三三星期星期四四星期星期五五星期星期六六12345678910111213141516171819202122232425262728293031（3）（3）左上右下对角线左上右下对角线上三个相邻数上三个相邻数右下者比左上者多右下者比左上者多8aa+8规律三规律三:

a-8能用字母表示吗能用字母表示吗?

星期星期日日星期星期一一星期星期二二星期星期三三星期星期四四星期星期五五星期星期六六12345678910111213141516171819202122232425262728293031规律四规律四:

a-6aa+6（4）（4）左下右上对角左下右上对角线上三个相邻数线上三个相邻数左下者比右上者多左下者比右上者多6能用字母表示吗能用字母表示吗?

星期星期日日星期星期一一星期星期二二星期星期三三星期星期四四星期星期五五星期星期六六12345678910111213141516171819202122232425262728293031日历中相邻三数之日历中相邻三数之间有什么间有什么相等关系相等关系？

规律五规律五:

同一直线上无论位置怎样的相邻三同一直线上无论位置怎样的相邻三个数，个数，首尾两数之和首尾两数之和=2X2X中间数中间数怎样用字母来表示和验证呢?

探究二探究二:

（1）水平三邻数水平三邻数:

a-1aa+1

（2）竖直三邻数竖直三邻数:

aa-7a+7（3）斜下三邻数斜下三邻数:

aa+8a-8（4）斜上三邻数斜上三邻数a-6aa+6（a-1）+（a+1）=_2a（a-7）+（a+7）=_2a（a-8）+（a+8）=_2a（a-6）+（a+6）=_2a在日历中，同一直线上无论位置怎样的相邻三个数，首尾两数之和都等于中间数的2倍。

注意哦!

对探索到的规律既要能用文字叙述它，又要会用字母来表示和验证它!

星期日星期日星期一星期一星期二星期二星期三星期三星期四星期四星期五星期五星期六星期六12345678910111213141516171819202122232425262728293031

（1）日历中日历中33方框内方框内九数之九数之和和与方框中与方框中正中间的数正中间的数有何等有何等量关系？

量关系？

规律六规律六:

正方形方框中正方形方框中九数之和九数之和=9中间数中间数探究三探究三:

星期日星期日星期一星期一星期二星期二星期三星期三星期四星期四星期五星期五星期六星期六12345678910111213141516171819202122232425262728293031

（2）这个关系在这个关系在其它方框其它方框中成立吗中成立吗?

九数之和九数之和=9X中间数中间数答:

成立!

（3）这个关系对这个关系对任何一个月任何一个月的日的日历都成立吗历都成立吗?

九数之和九数之和=9X中间数中间数2013年年2月月日历日历日日一一二二三三四四五五六六12345678910111213141516171819202122232425262728答:

2013年年2月月日历日历星期日星期日星期一星期一星期二星期二星期三星期三星期四星期四星期五星期五星期六星期六12345678910111213141516171819202122232425262728（4）这个规律也能用字母表示吗这个规律也能用字母表示吗?

aa-8a-7a-6a-1a+1a+6a+7a+8看的更清楚看的更清楚:

相对相对的两个数的的两个数的和和为为2a（中间数的中间数的2倍倍）,总和为总和为9a.证明：

证明：

9个数总和个数总和:

（a-8）+（a-7）+（a-6）+（a-1）+a+（a+1）+（a+6）+（a+7）+（a+8）9a我们来我们来证明刚证明刚才得到才得到结论：

结论：

aa-7a+8a-6a-8a+6a+7a-1a+1（a-8）+（a-7）+（a-6）+（a-1）+a+（a+1）（a+6）+（a+7）+（a+8）=_9a在正方形方框中，设中间的一个数为a，那么，其余八个数分别应怎样表示?

所以，正方形方框中，九数之和等于中间数的九倍。

（5）你还能发现正方形方框中九数之间的其它关系吗?

aa-7a+8a-6a-8a+6a+7a-1a+110119171816234变式探究巩固提高探究四探究四:

2013年年7月月日历日历星期星期日日星期星期一一星期星期二二星期星期三三星期星期四四星期星期五五星期星期六六12345678910111213141516171819202122232425262728293031变式探究变式探究

（1）在在+字形区域内，字形区域内，五个数五个数之和之和与与正中心正中心何关系何关系?

能用字能用字母表示并验证这个关系吗母表示并验证这个关系吗?

答答:

五数之和五数之和=5中间数中间数aa+1a-1a+7a-7（a-1）+（a+1）+a+（a-7）+（a+7）=_5a2013年年7月月日历日历星期星期日日星期星期一一星期星期二二星期星期三三星期星期四四星期星期五五星期星期六六12345678910111213141516171819202122232425262728293031变式探变式探究究

（2）在在H形区域内，形区域内，七个数之和七个数之和与与正中心的数正中心的数有有关系关系?

能用字母表示吗能用字母表示吗?

七数之和七数之和=7中间数中间数aa-1a+1a-8a+6a-6a+8（a-8）+（a+8）+（a-1）+（a+1）+a+（a-6）+（a+6）=7a1、按左图方式摆放餐桌和椅子按左图方式摆放餐桌和椅子

（1）1张餐桌可坐张餐桌可坐_人人;

2张餐桌可坐张餐桌可坐_人人.

（2）按照左图的方式继续排列按照左图的方式继续排列餐桌餐桌,完成下表完成下表:

桌子桌子张数张数12345n可坐可坐人数人数610141822610试一试44+4+4+4（4n+2）n张餐桌可坐张餐桌可坐人人用火柴棒按下图的方式搭三角形用火柴棒按下图的方式搭三角形.三角形三角形个数个数12345n火柴棒火柴棒根数根数填写下表填写下表:

357911活动二3+2+2+2+2+21+2三角形个数三角形个数12345n火柴棒根数火柴棒根数3579112n+13=1+25=1+2+27=1+2+2+29=1+2+2+2+211=1+2+2+2+2+2=1+2+2+2+2+2+2+21+2n三角形个数三角形个数火柴棒根数火柴棒根数12345n3n+15n+2用火柴棍拼接成如图所示的图形，用火柴棍拼接成如图所示的图形，请问拼接请问拼接n个这样的图形要多少根火柴？

个这样的图形要多少根火柴？

n个个图图1图图2火柴根数火柴根数规律规律：

每增加每增加1个个图形要添图形要添3根火柴根火柴规律规律：

每每增加增加1个个图形要添图形要添5根火柴根火柴4n+2n块灰色瓷砖块灰色瓷砖白瓷砖块数白瓷砖块数如图拼接瓷砖如图拼接瓷砖,如果用了如果用了n块块灰色瓷砖灰色瓷砖,需要多少块白瓷砖？

需要多少块白瓷砖？

规律规律：

每增加：

每增加1块块瓷砖要增加瓷砖要增加4块块瓷瓷砖砖白色白色灰色灰色2.用大小相等的小正方形拼大正方形，拼用大小相等的小正方形拼大正方形，拼第一个正方形需要第一个正方形需要4个小正方形，拼第二个正方形需要个小正方形，拼第二个正方形需要9个小正个小正方形，拼一拼，想一想，按照这样的方法拼成的第方形，拼一拼，想一想，按照这样的方法拼成的第n个正方形个正方形比第（比第（n-1）个正方形多几个正方形？

）个正方形多几个正方形？

思路思路：

先从个数少的先从个数少的依次进行探索，列出表依次进行探索，列出表格，填入数据，观察、格，填入数据，观察、思考寻找问题的规律，思考寻找问题的规律，大胆进行猜想、验证。

大胆进行猜想、验证。

第第11个个正方形正方形第第22个个正方形正方形第第33个个正方形正方形拼成的拼成的正方形正方形第第11个个第第22个个第第33个个第第44个个第第nn个个含小正含小正方形个数方形个数数字规律数字规律比前一个多比前一个多数字规律数字规律（1111+1+1+1+1）2491625579（2222+1+1+1+1）2（3333+1+1+1+1）2（4444+1+1+1+1）2（nnnn+1+1+1+1）2?

22+123+124+12n+1猜想猜想321+1练一练练一练

（2）：

）：

如图是如图是2002年年6月的日历。

现月的日历。

现用一个矩形在日用一个矩形在日历中任意框出历中任意框出4个个数，数，请你用一个等式表请你用一个等式表示示a、b、c、d之之间的关系：

间的关系：

。

ababcdcda+d=b+ca-c=b-dababcdcd33、研究下列算式，你发现了什么规律？

、研究下列算式，你发现了什么规律？

用字母表示这个规律用字母表示这个规律.113+1=23+1=222；

224+1=34+1=322；

335+1=45+1=422；

446+1=56+1=522；

用用nn表示自然数表示自然数,规律规律是：

是：

n（n+2）+1=（n+1）244、请你推断第请你推断第77个数是个数是。

小小结结通过具体数值发现发现规律规律用字母来表示表示规律规律符号运算验证验证规律规律观察分析对比概括通过本节课你有哪些收获?

（1）在下列表格中前面所探究的规律是否正确在下列表格中前面所探究的规律是否正确?

1234567891011121